- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основные правила дифференцирования
Содержание
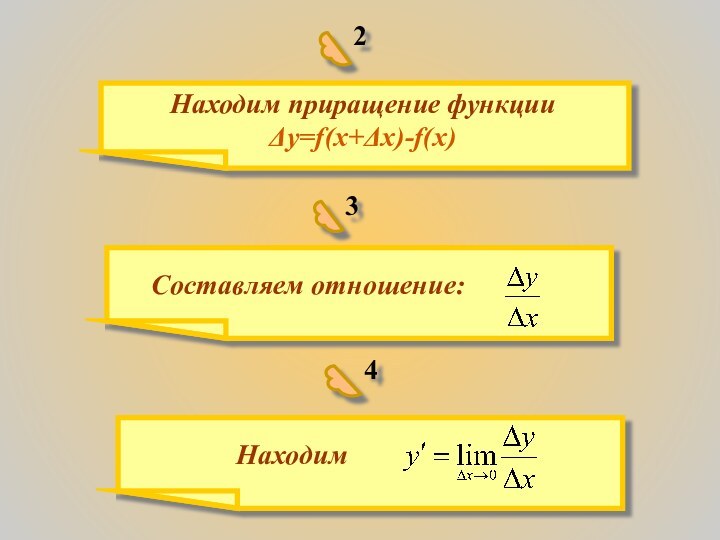
- 2. Находим приращение функции Δy=f(x+Δx)-f(x) 23 Составляем отношение:4 Находим
- 3. ПРИМЕР.Найдем производную функцииДадим аргументу х приращение Δх и найдем значение функции y+Δy: 12Находим приращение функции
- 4. 3Составляем отношение
- 5. Находим4Полученный результат является частным случаем производной от степенной функцииМожно показать, что в общем случае
- 6. производная степенной функции
- 7. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ1Производная постоянной величины равна 0:2Производная аргумента равна 1:
- 8. 3Производная алгебраической суммы (разности) конечного числа дифференцируемых функций равна сумме (разности) производных этих функций:
- 9. ДОКАЗАТЕЛЬСТВО:Пусть u=u(x) и v=v(x) -дифференцируемые функции.Найдем производную
- 10. Находим приращение функцииСоставляем отношениеНаходим предел этого отношения:
- 11. 4Производная произведения двух дифференцируемых функций равна сумме
- 12. ДОКАЗАТЕЛЬСТВО:Пусть u=u(x) и v=v(x) -дифференцируемые функции.Найдем производную
- 13. Находим приращение функцииСоставляем отношение
- 14. Находим предел этого отношения:Имеем по определению производной:
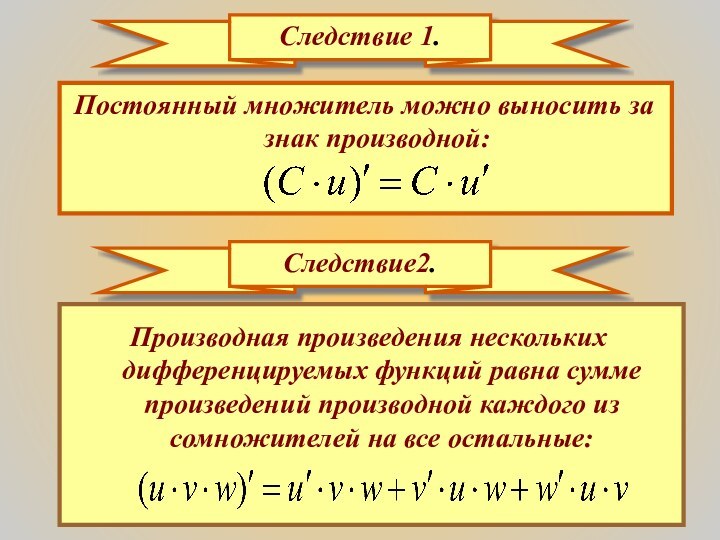
- 15. Следствие 1.Постоянный множитель можно выносить за знак
- 16. 5Производная частного двух дифференцируемых функций находится по формуле:
- 17. ПРИМЕРЫ.1Найти производную функциии вычислить ее значение в точке х=1.
- 18. Решение.Находим значение производной в точке х=1:
- 19. 2Найти производную функциии вычислить ее значение в точке х=1.
- 20. Решение.Находим значение производной в точке х=1:
- 21. 3Найти производную функциии вычислить ее значение в точке х=1.
- 22. Скачать презентацию
- 23. Похожие презентации
Находим приращение функции Δy=f(x+Δx)-f(x) 23 Составляем отношение:4 Находим