Презентация на тему Графики прямой и обратной пропорциональности

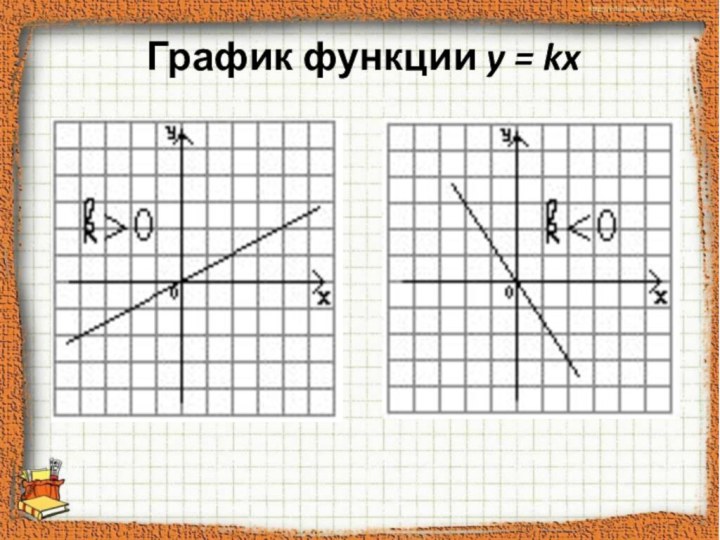
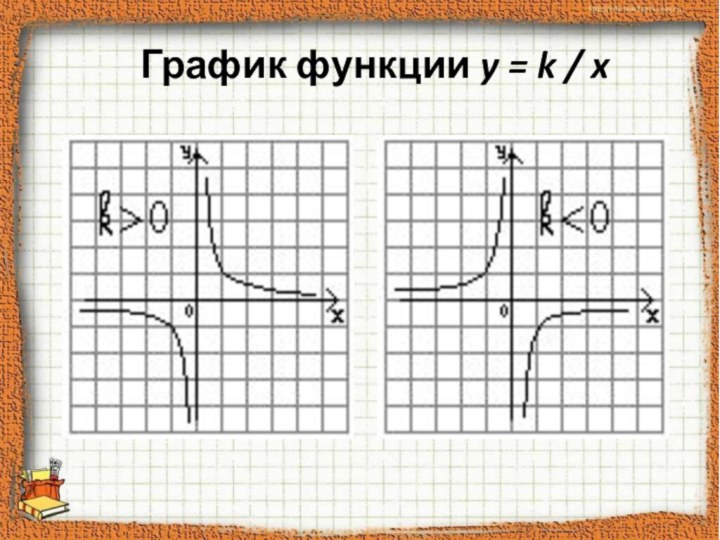
прямой и обратной пропорциональности, закрепить навыки построения графиков;
Формировать потребность

приобретения новых знаний, создать условия для контроля (самоконтроля) усвоения умений и навыков;
Развивать зрительную память, внимание, умение анализировать, сравнивать, обобщать.

делать выводы;
побуждать учеников к самоконтролю и взаимоконтролю;
формировать навыки грамотного

построения графиков;
воспитание интереса к математике.

обратной пропорциональности (презентация).
Правила построения графиков функций прямой и обратной

пропорциональности (буклет).
Описать свойства и построить графики функции прямой пропорциональности (доклад).
Описать свойства и построить график функции обратной пропорциональности (доклад).
Составить кроссворд.

- я запоминаю;
Я делаю, - я усваиваю.»

из которых примем за 1 кв. единицу. Какова площадь

такого прямоугольника? Длина х, ширина у. Составим формулу зависимости у от х.

b называется линейной функцией, где k, b - числа

(параметры), x - переменная (аргумент)
Линейная функция вида y = kx называется прямой пропорциональностью.

Корни: x = 0
3. При k > 0 ⇒

y > 0 при x ∈ (0;+∞)
y < 0 при x ∈ (-∞; 0)
При k < 0 ⇒ y > 0 при x ∈ (-∞; 0)
y < 0 при x ∈ (0;+∞)
4. При k > 0 ⇒ функция возрастает
При k < 0 ⇒ функция убывает
5. Экстремумов нет.
6. Наибольшего и наименьшего значения нет.
7. Ey = R
8. Нечётная, непериодическая.
 
График - прямая, строим по двум точкам.

  Замечание: График функции y = kx + b получаем перемещением графика функции y = kx по вертикали:
если b > 0 , то вверх на b
если b < 0 , то вниз на b

x называется обратной пропорциональностью.

= (-∞; 0)∪ (0; +∞)
2. Корней нет
3. При k

> 0 ⇒ y > 0 при x ∈ (0;+∞)
y < 0 при x ∈ (-∞; 0)
При k < 0 ⇒ y > 0 при x ∈ (-∞; 0)
y < 0 при x ∈ (0;+∞)
4. При k > 0 ⇒ функция убывает
При k < 0 ⇒ функция возрастает
5. Экстремумов нет.
6. Наибольшего и наименьшего значения нет.
7. Ey = (-∞; 0)∪ (0; +∞)
8. Нечётная, непериодическая.
 
График - гипербола, строим заполняя таблицу.

у=k/x
3. Если график функции y=k/x расположен во II и

IV четвертях к.п., то k … нуля
4. Функция, заданная формулой y = kx + b
5. Если график функции y=k/x расположен в I и III четвертях к.п., то k … нуля
6. Точка, не входящая в область определения функции y=k/x
7. Из них состоит гипербола