Презентация на тему Преобразование графиковфункций

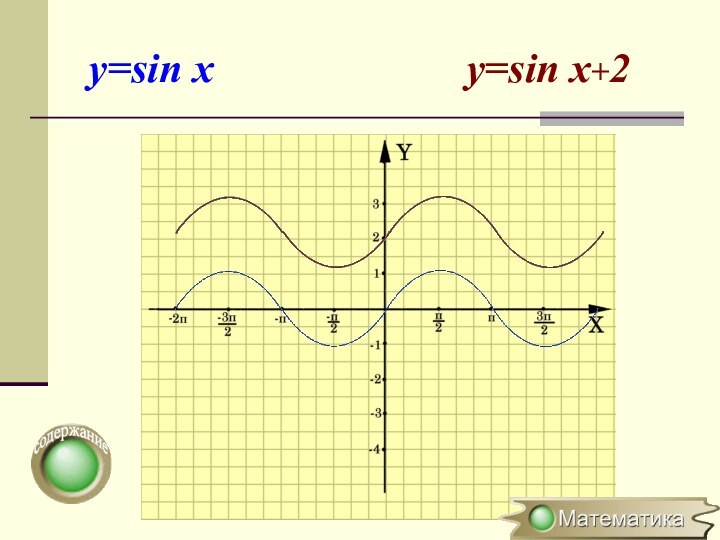
OY
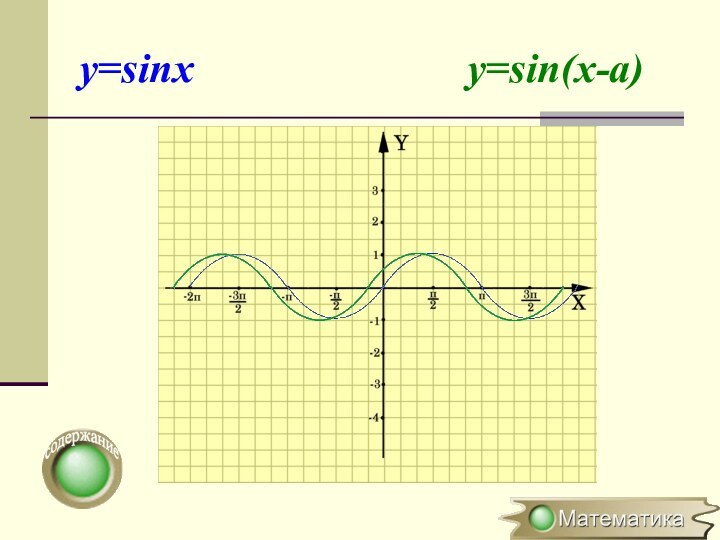
Параллельный перенос вдоль оси ОХ
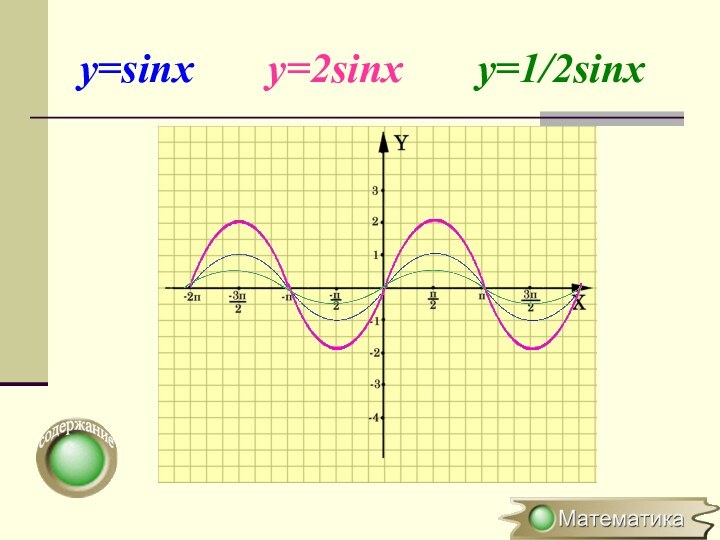
Растяжение (сжатие) в Растяжение (сжатие)

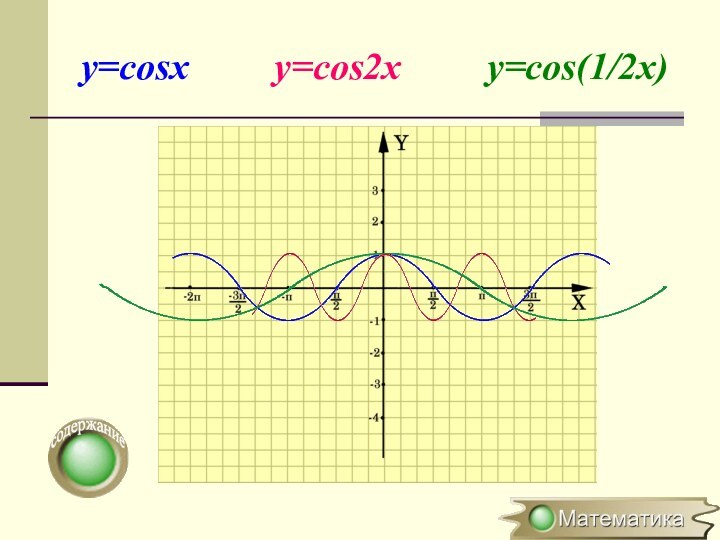
в k Растяжение (сжатие) в k раз вдоль оси Растяжение (сжатие) в k раз вдоль оси OY
Растяжение (сжатие) в Растяжение (сжатие) в k Растяжение (сжатие) в k раз вдоль оси Растяжение (сжатие) в k раз вдоль оси OРастяжение (сжатие) в k раз вдоль оси OХ
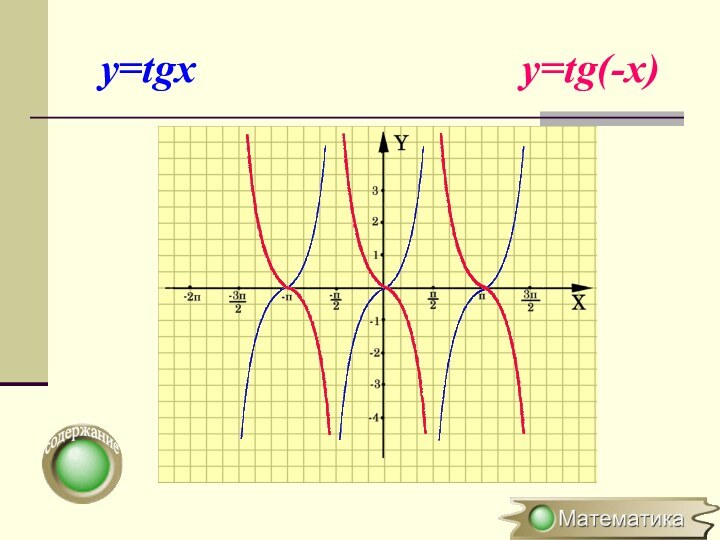
Симметричное отображение относительно Симметричное отображение относительно Симметричное отображение относительно оси Симметричное отображение относительно оси OY
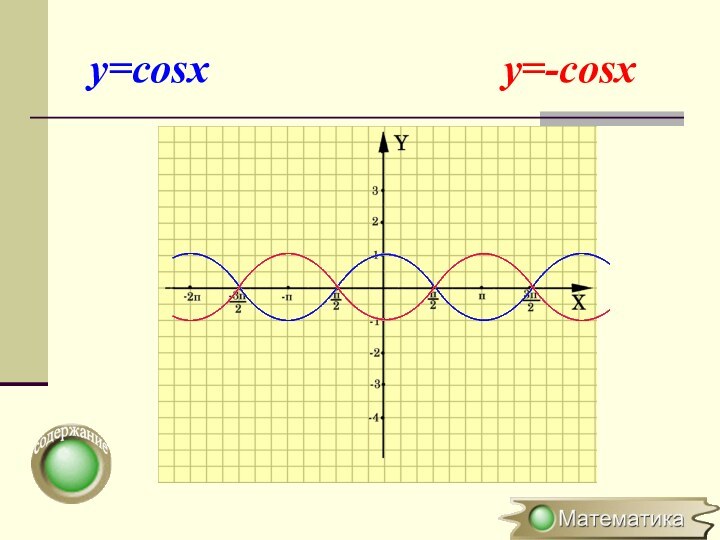
Симметричное отображение относительно Симметричное отображение относительно Симметричное отображение относительно оси Симметричное отображение относительно оси OX
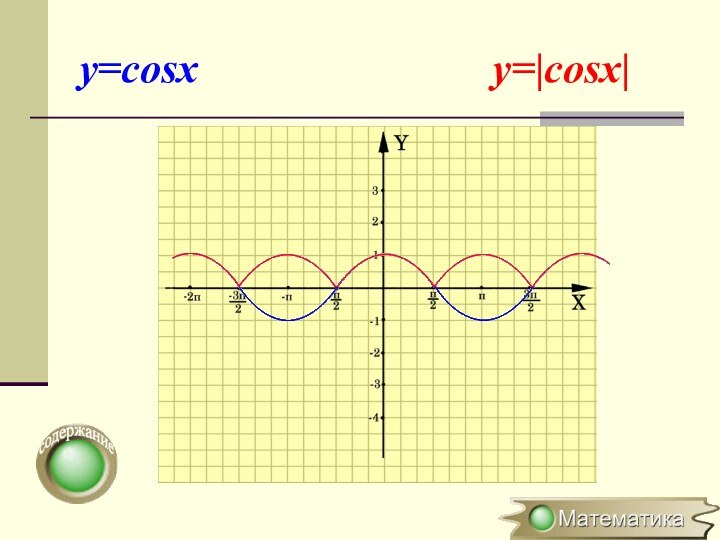
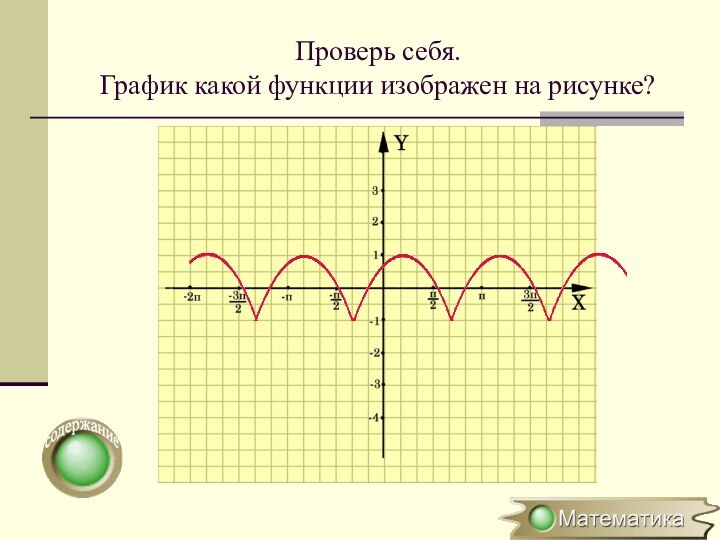
Построение графика y=|f(x)|
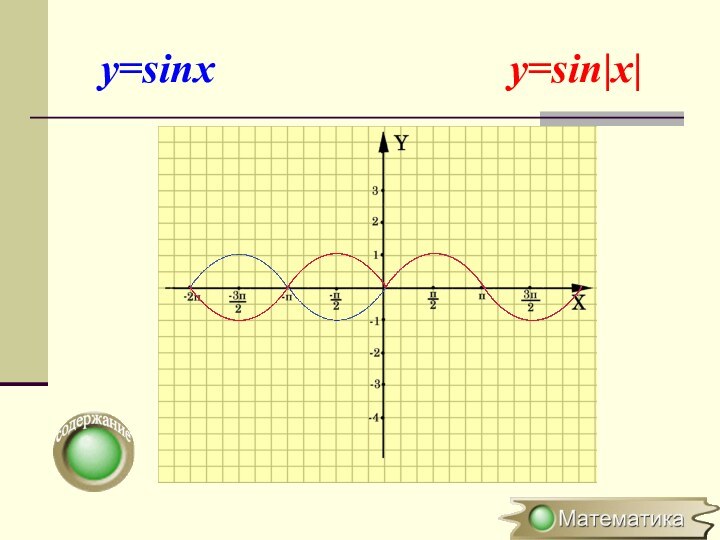
Построение графика y=f(|x|)

OY
y=f(x) → y=f(x)+a

(x0;y0) → (x0;y0+a)

Для построения графика функции y=f(x)+a необходимо график функции y=f(x) перенести вдоль оси OY на вектор (0;а)

y=sin x+2

y=f(x) → y=f(x-a)
(x0;y0)

→ (x0+a;y0)

Для построения графика функции y=f(x-a) необходимо график функции y=f(x) перенести вдоль оси OX на вектор (0;а)

y=sin(x-a)

y=f(x) → y=kf(x), где k>0

(x0;y0) → (x0;ky0)

Для построения графика функции y=kf(x) необходимо график функции y=f(x) растянуть в k раз вдоль оси ОY для k >1 или сжать в 1/k развдоль оси OY для k<1

y=1/2sinx

y=f(x) → y=f(kx), где k>0

(x0;y0) → ( x0;y0)

Для построения графика функции y=f(kx) необходимо график функции y=f(x) сжать в k раз вдоль оси ОХ для k >1 или растянуть в 1/k раз вдоль оси OХ для k<1

y=cos(1/2x)

y=-f(x)
(x0;y0) → (x0;-y0)


Для построения

графика функции y=-f(x) необходимо график функции y=f(x)симметрично отобразить относительно оси ОХ

y=-cosx

→ y=f(-x)
(x0;y0) → (-x0;y0)


Для построения

графика функции y=f(-x) необходимо график функции y=f(x) симметрично отобразить относительно
оси ОY

y=tg(-x)

y=|f(x)| необходимо часть графика функции y=f(x), лежащую выше оси

OX, оставить неизменной, а часть графика y=f(x), лежащую ниже оси OХ, симметрично отобразить относительно оси ОХ

f(x), если х 0
y=|f(x)|=
-f(x), если х < 0

y=|cosx|

f(x), если х 0
y=f(|x|)=
f(-x), если х<0


Для построения графика функции y=|f(x)| необходимо часть графика функции y=f(x), лежащую правее оси OY, оставить неизменной, а часть графика y=f(x), лежащую левее оси OY, симметрично отобразить относительно оси ОY

y=sin|x|