- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему 9 класс Урок Функция и его свойства
Содержание
- 2. СодержаниеЦели урокаОпределениеВиды функцийСвойства функцийЗадание 1Задание 2Тест
- 3. Цели урокаЗакрепление свойств функцииРазвитие умений исследования графиков функцииВыполнение упражнений и построение графиков функций
- 4. Функция – зависимость одной переменной от другой,
- 5. Виды функцийЛинейнаяПрямая пропорциональностьОбратная пропорциональностьКвадратичнаяКвадратный кореньМодуль Другие функции
- 6. Свойства функцийОбласть определения функцииМножество значений функцииМонотонностьЧетностьОграниченностьНаибольшее, наименьшее значениеТочки экстремумаВыпуклостьПересечение с осями координатПромежутки знакопостоянства
- 7. Задание 1Изобразите схематически графики функций
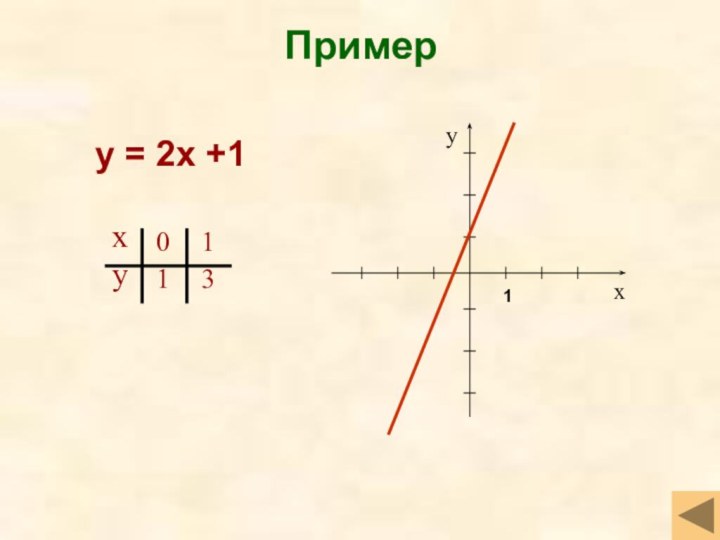
- 8. Примеру = 2х +11
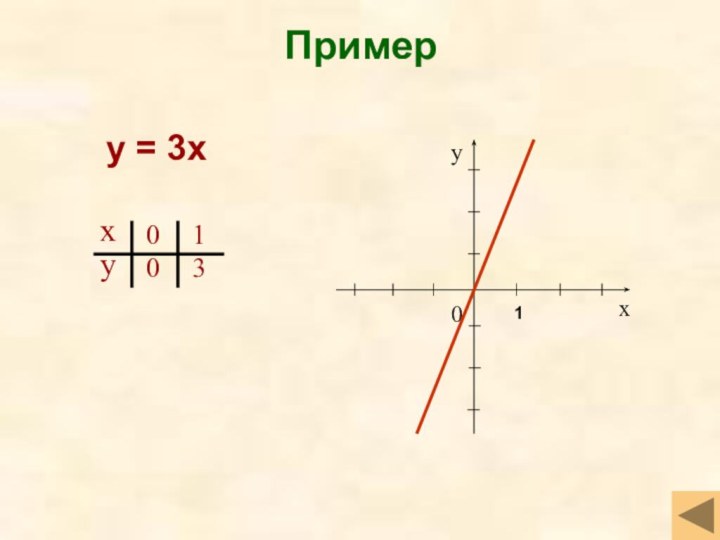
- 9. Примеру = 3х1
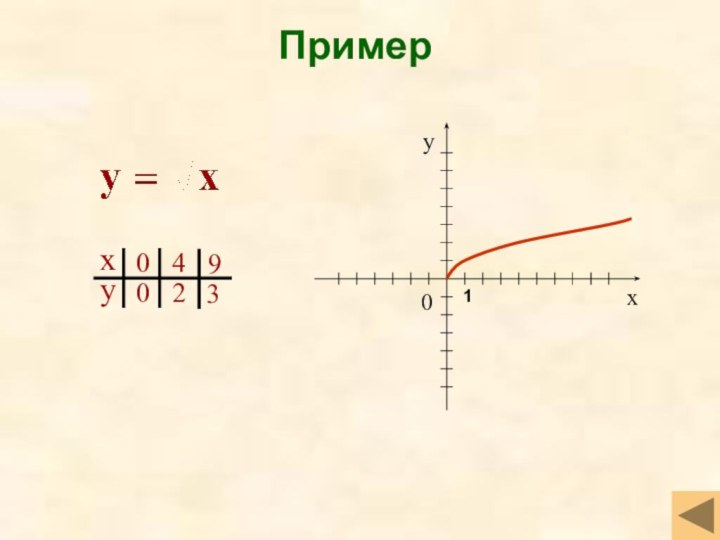
- 10. Пример1
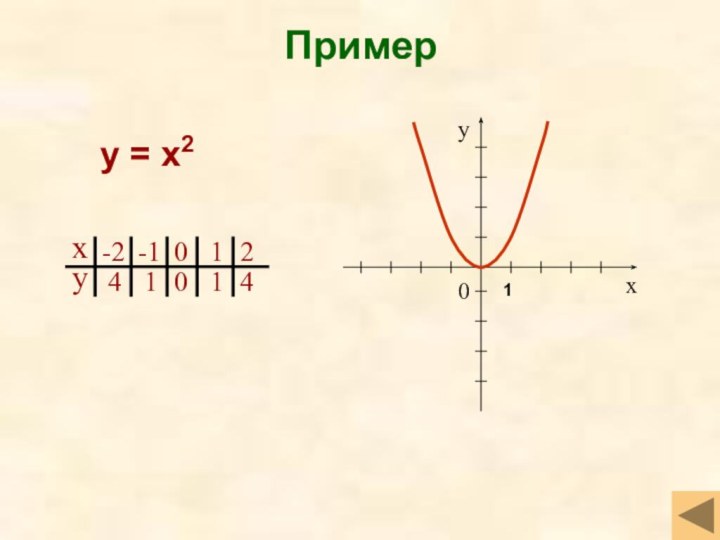
- 11. Примеру = х21
- 12. Пример1
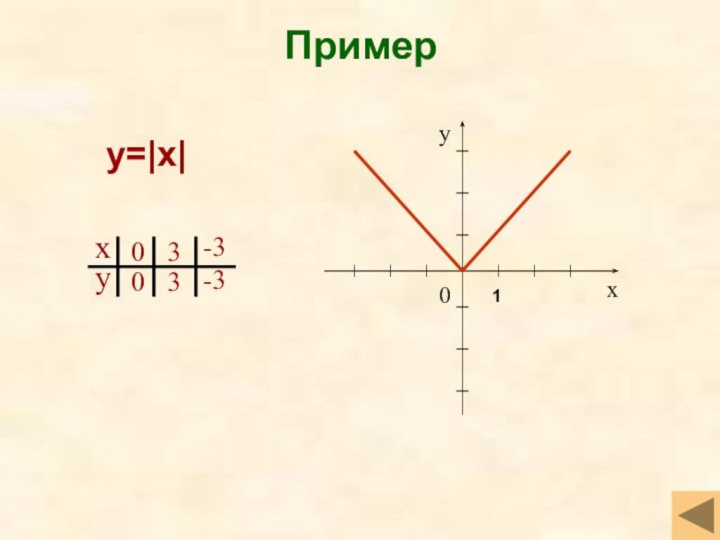
- 13. Примерy=|x|1
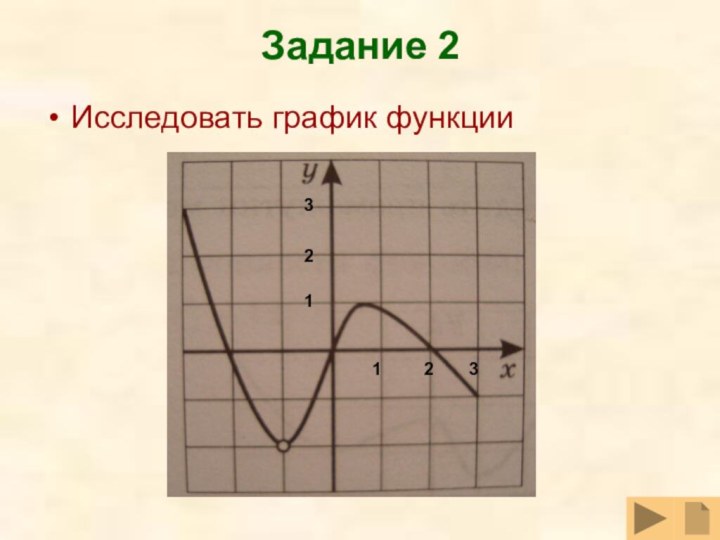
- 14. Задание 2Исследовать график функции121233
- 15. Тест1. Найдите область определения функции
- 16. 2. Исследуйте на ограниченность функциюа) ограничена сверхуб)
- 17. 3. Среди заданных функций укажите возрастающиеа) 2, 4б) 1, 2, 4в) 3г) 1, 2
- 18. 4. Среди заданных функций укажите убывающиеа) 1, 3б) 3в) 3, 4г) 1
- 19. 5. Среди заданных функций укажите четныеа) 1, 3б) 1, 2в) 3, 4г) 1, 4
- 20. 6. Среди заданных функций укажите нечетныеа) 1, 3б) 2, 4в) 2, 3г) 3, 4
- 21. 7. Найдите множество значений функций
- 22. Верно
- 23. Не верно
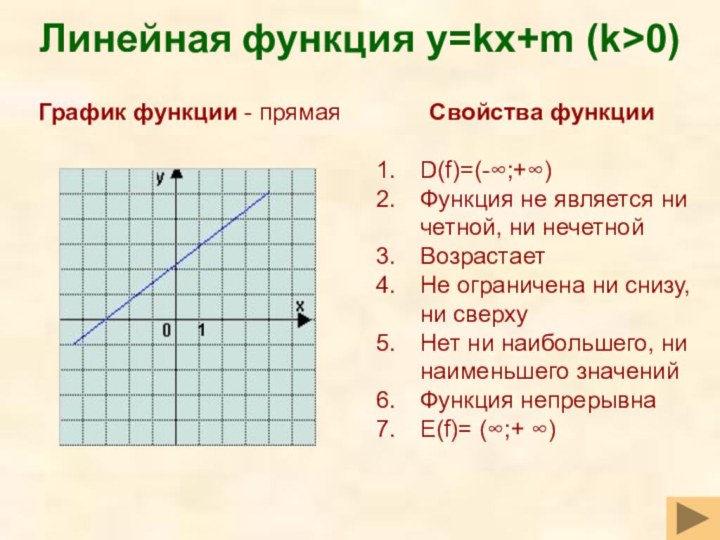
- 24. Линейная функция y=kх+m (k>0)Свойства функцииD(f)=(-∞;+∞)Функция не является
- 25. Линейная функция y=kx+m (k
- 26. Прямая пропорциональность y=kx (k>0) Свойства функцииD(f)=(-∞;+∞)Функция является
- 27. Прямая пропорциональность y=kx (k
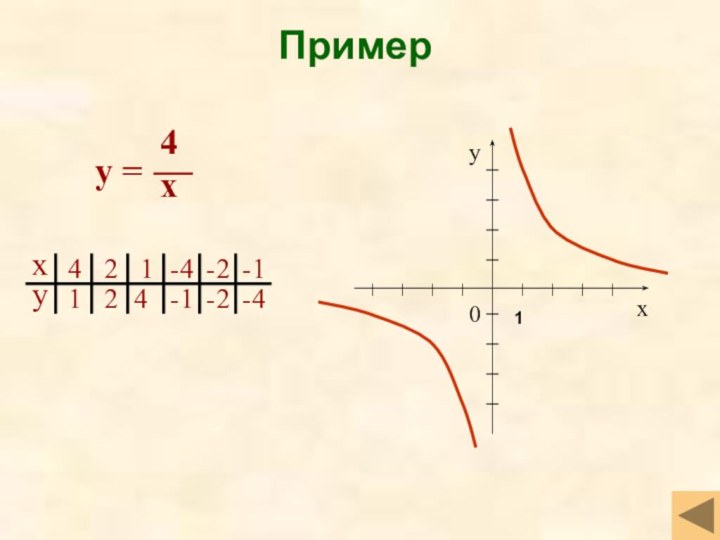
- 28. Обратная пропорциональность (k>0) Свойства функцииD(f)=(-∞;0)U(0;+∞)НечётнаяУбывает на открытом луче
- 29. Обратная пропорциональность (k0, выпукла вниз при x
- 30. Квадратичная функция y=kx2 (k>0) Свойства функцииD(f)=(-∞;+∞)ЧётнаяУбывает на
- 31. Квадратичная функция y=kx2 (k
- 32. Квадратичная функция y=ax2+bx+c (a>0)Свойства функцииD(f)=(-∞;+∞)Убывает на луче
- 33. Квадратичная функция y=ax2+bx+c (a
- 34. Квадратный кореньСвойства функцииD(f)=[0;+∞)Не является ни четной, ни
- 35. Модуль y=|x| Свойства функцииD(f)=(-∞;+∞)ЧётнаяУбывает на луче (-∞;0], возрастает
- 36. Функция y=x2n+1 (n N) Свойства функцииD(f)=(-∞;+∞)НечётнаяВозрастаетНе ограничена
- 37. Функция y=x-(2n+1) Свойства функцииD(f)=(-∞;0)U(0;+∞)НечётнаяУбывает на открытом луче
- 38. Функция y=x-2n Свойства функцииD(f)=(-∞;0)U(0;+∞)ЧётнаяВозрастает на открытом луче
- 39. Скачать презентацию
- 40. Похожие презентации
















![Презентация 9 класс Урок Функция и его свойства Квадратичная функция y=kx2 (k>0) Свойства функцииD(f)=(-∞;+∞)ЧётнаяУбывает на луче (-∞;0], возрастает на луче](/img/tmb/7/605118/75516aff59013ec7aa0ab8880016737e-720x.jpg)
![Презентация 9 класс Урок Функция и его свойства Квадратичная функция y=ax2+bx+c (a>0)Свойства функцииD(f)=(-∞;+∞)Убывает на луче (-∞; ],](/img/tmb/7/605118/04e55d6b39cfcb2b6d89b691b7ed2858-720x.jpg)
![Презентация 9 класс Урок Функция и его свойства Модуль y=|x| Свойства функцииD(f)=(-∞;+∞)ЧётнаяУбывает на луче (-∞;0], возрастает на луче [0;+∞)Ограничена снизу, не](/img/tmb/7/605118/f33e568c9cf3da39e3a4d00721bfe605-720x.jpg)

![Презентация 9 класс Урок Функция и его свойства Функция y=x2n (n N)Свойства функцииD(f)=(-∞;+∞)ЧётнаяУбывает на луче (-∞;0], возрастает на луче](/img/tmb/7/605118/ab3515a6664d18d1195361bf28952601-720x.jpg)
Слайд 3
Цели урока
Закрепление свойств функции
Развитие умений исследования графиков функции
Выполнение
упражнений и построение графиков функций
Слайд 4 Функция – зависимость одной переменной от другой, причем
для любых значений х соответствует единственное значение функции y.
График
функции – множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты соответствующим значениям функции.Определение
Слайд 5
Виды функций
Линейная
Прямая пропорциональность
Обратная пропорциональность
Квадратичная
Квадратный корень
Модуль
Другие функции
Слайд 6
Свойства функций
Область определения функции
Множество значений функции
Монотонность
Четность
Ограниченность
Наибольшее, наименьшее значение
Точки
экстремума
Выпуклость
Пересечение с осями координат
Промежутки знакопостоянства
Слайд 16
2. Исследуйте на ограниченность функцию
а) ограничена сверху
б) ограничена
снизу
в) ограничена снизу и сверху
г) не ограничена ни снизу,
ни сверху
Слайд 24
Линейная функция y=kх+m (k>0)
Свойства функции
D(f)=(-∞;+∞)
Функция не является ни
четной, ни нечетной
Возрастает
Не ограничена ни снизу, ни сверху
Нет ни
наибольшего, ни наименьшего значенийФункция непрерывна
Е(f)= (∞;+ ∞)
График функции - прямая
1
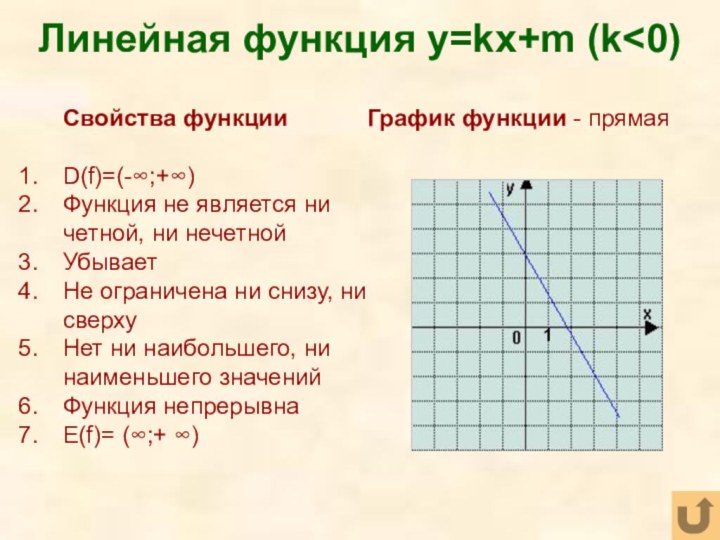
Слайд 25 Линейная функция y=kx+m (k
четной, ни нечетной
Убывает
Не ограничена ни снизу, ни сверху
Нет ни
наибольшего, ни наименьшего значенийФункция непрерывна
Е(f)= (∞;+ ∞)
График функции - прямая
1
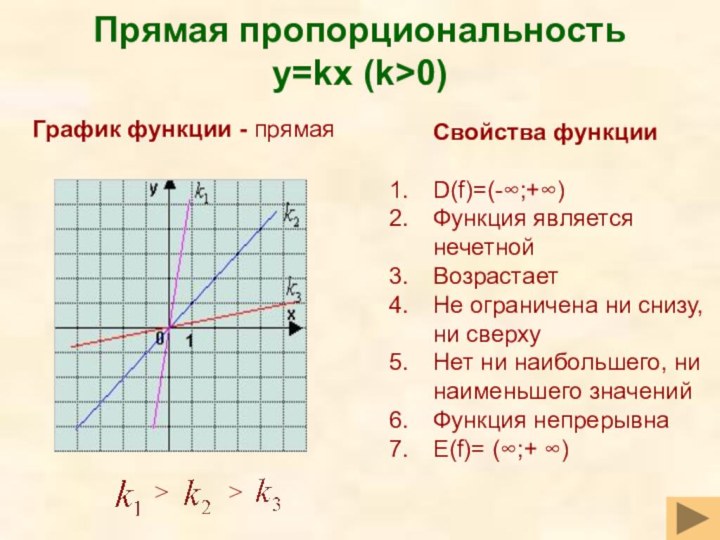
Слайд 26
Прямая пропорциональность
y=kx (k>0)
Свойства функции
D(f)=(-∞;+∞)
Функция является нечетной
Возрастает
Не ограничена
ни снизу, ни сверху
Нет ни наибольшего, ни наименьшего значений
Функция
непрерывнаЕ(f)= (∞;+ ∞)
>
>
График функции - прямая
1
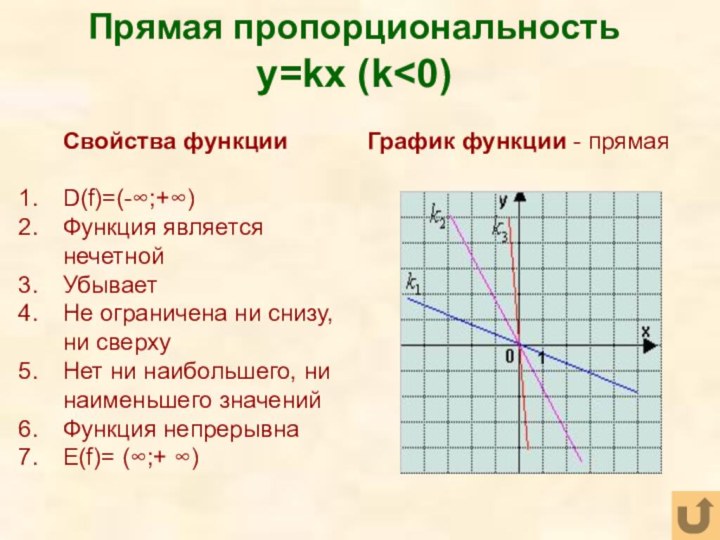
Слайд 27 Прямая пропорциональность y=kx (k
ни снизу, ни сверху
Нет ни наибольшего, ни наименьшего значений
Функция
непрерывнаЕ(f)= (∞;+ ∞)
График функции - прямая
1
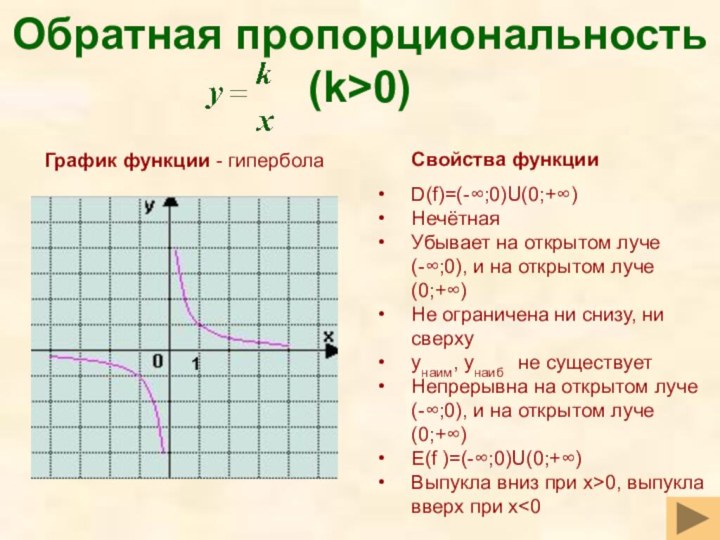
Слайд 28
Обратная пропорциональность (k>0)
Свойства функции
D(f)=(-∞;0)U(0;+∞)
Нечётная
Убывает на открытом луче
(-∞;0), и на открытом луче (0;+∞)
Не
ограничена ни снизу, ни сверхуyнаим, yнаиб не существует
Непрерывна на открытом луче (-∞;0), и на открытом луче (0;+∞)
E(f )=(-∞;0)U(0;+∞)
Выпукла вниз при x>0, выпукла вверх при x<0
График функции - гипербола
1
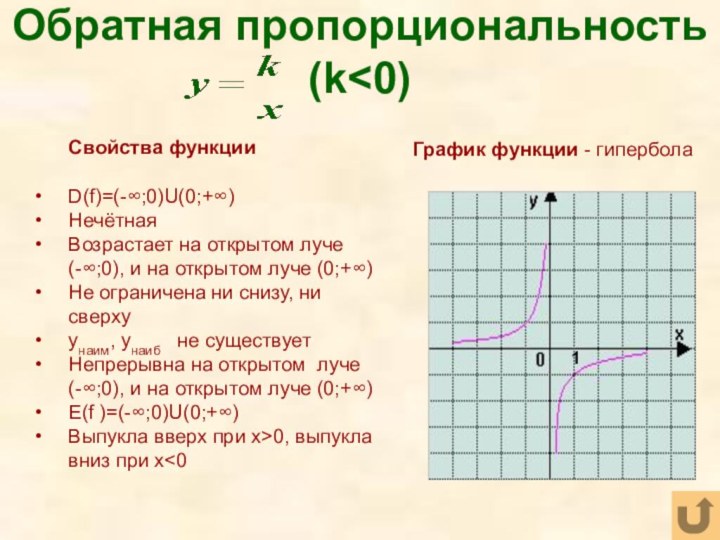
Слайд 29 Обратная пропорциональность (k
на открытом луче (-∞;0), и
на открытом луче (0;+∞)Не ограничена ни снизу, ни сверху
yнаим, yнаиб не существует
Непрерывна на открытом луче (-∞;0), и на открытом луче (0;+∞)
E(f )=(-∞;0)U(0;+∞)
Выпукла вверх при x>0, выпукла вниз при x<0
График функции - гипербола
1
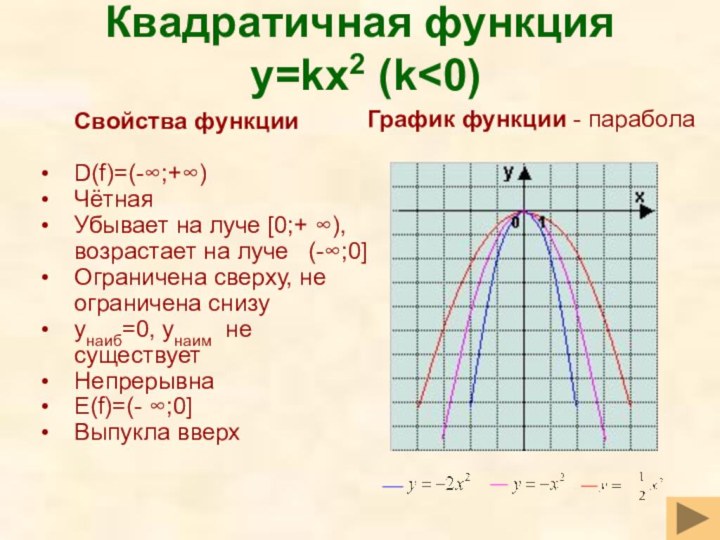
Слайд 30
Квадратичная функция
y=kx2 (k>0)
Свойства функции
D(f)=(-∞;+∞)
Чётная
Убывает на луче (-∞;0],
возрастает на луче [0;+∞)
Ограничена снизу, не ограничена сверху
yнаим=0, yнаиб
не существуетНепрерывна
E(f)=[0;+∞)
Выпукла вниз
График функции - парабола
Слайд 31 Квадратичная функция y=kx2 (k
∞), возрастает на луче (-∞;0]
Ограничена сверху, не ограничена
снизуyнаиб=0, yнаим не существует
Непрерывна
E(f)=(- ∞;0]
Выпукла вверх
График функции - парабола
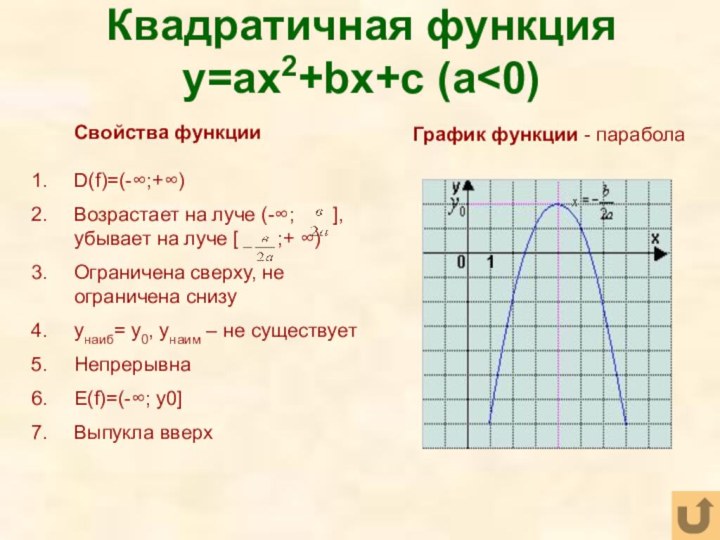
Слайд 32
Квадратичная функция y=ax2+bx+c (a>0)
Свойства функции
D(f)=(-∞;+∞)
Убывает на луче (-∞;
], возрастает на луче [
; + ∞)Ограничена снизу, не ограничена сверху
yнаим= y0 , yнаиб – не существует
Непрерывна
E(f)=[y0 ;+∞)
Выпукла вниз
График функции - парабола
1
Слайд 33 Квадратичная функция y=ax2+bx+c (a
], убывает на луче [
;+ ∞)Ограничена сверху, не ограничена снизу
yнаиб= y0, yнаим – не существует
Непрерывна
E(f)=(-∞; y0]
Выпукла вверх
График функции - парабола
1
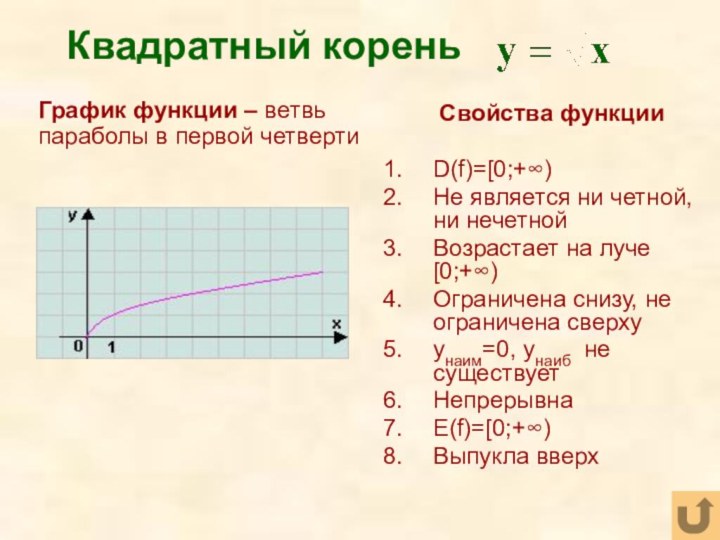
Слайд 34
Квадратный корень
Свойства функции
D(f)=[0;+∞)
Не является ни четной, ни нечетной
Возрастает
на луче [0;+∞)
Ограничена снизу, не ограничена сверху
yнаим=0, yнаиб не
существуетНепрерывна
E(f)=[0;+∞)
Выпукла вверх
График функции – ветвь параболы в первой четверти
Слайд 35
Модуль y=|x|
Свойства функции
D(f)=(-∞;+∞)
Чётная
Убывает на луче (-∞;0], возрастает на
луче [0;+∞)
Ограничена снизу, не ограничена сверху
yнаим=0, yнаиб не существует
Непрерывна
E(f)=[0;+∞)
Функцию
можно считать выпуклой вниз
Слайд 36
Функция y=x2n+1 (n N)
Свойства функции
D(f)=(-∞;+∞)
Нечётная
Возрастает
Не ограничена ни
снизу, ни сверху
yнаим, yнаиб не существует
Непрерывна
E(f )=(-∞;+∞)
Выпукла вверх при
x<0 Выпукла вниз при x>0График функции - кубическая парабола
Слайд 37
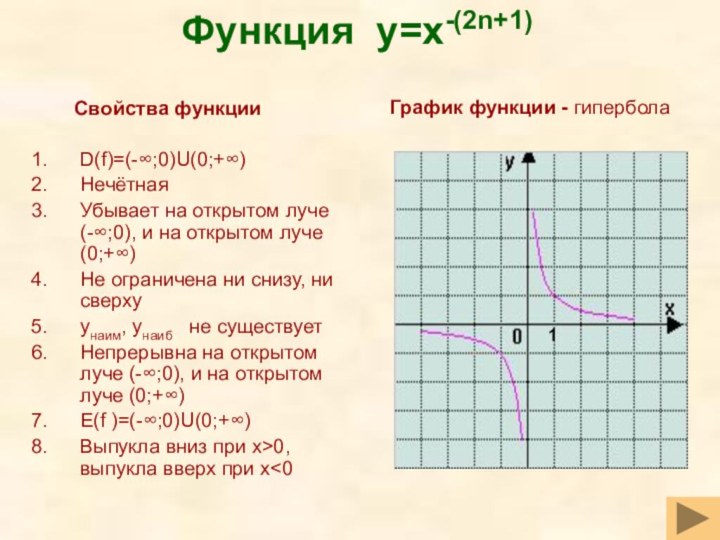
Функция y=x-(2n+1)
Свойства функции
D(f)=(-∞;0)U(0;+∞)
Нечётная
Убывает на открытом луче
(-∞;0), и на открытом луче (0;+∞)
Не ограничена
ни снизу, ни сверхуyнаим, yнаиб не существует
Непрерывна на открытом луче (-∞;0), и на открытом луче (0;+∞)
E(f )=(-∞;0)U(0;+∞)
Выпукла вниз при x>0, выпукла вверх при x<0
График функции - гипербола
1
Слайд 38
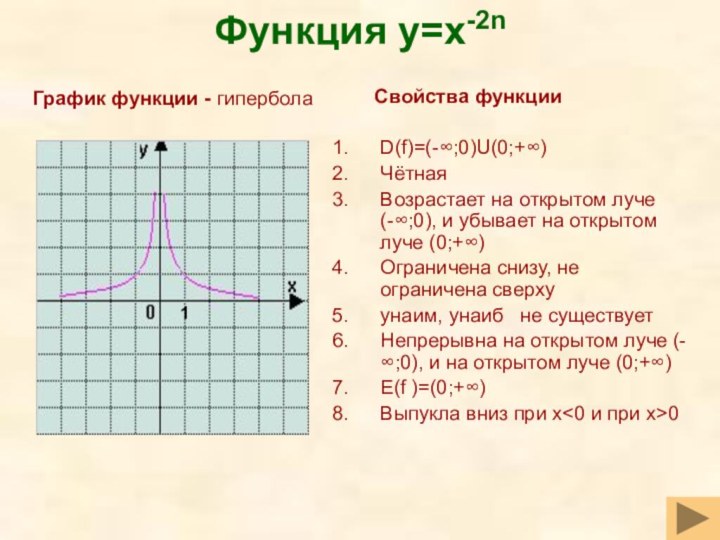
Функция y=x-2n
Свойства функции
D(f)=(-∞;0)U(0;+∞)
Чётная
Возрастает на открытом луче
(-∞;0), и убывает на открытом луче (0;+∞)
Ограничена
снизу, не ограничена сверхуyнаим, yнаиб не существует
Непрерывна на открытом луче (-∞;0), и на открытом луче (0;+∞)
E(f )=(0;+∞)
Выпукла вниз при x<0 и при x>0
График функции - гипербола
1





























