Слайд 2
Аннотация к проекту:
Цели проекта: 1)Расширить свои знания
о логарифмической функции
2)Рассмотреть применение логарифмов в практических приложениях и физических явлениях
3)С помощью специальных формул перевести нотную
грамоту на язык логарифмов
Гипотеза: Удивительное рядом…
Краткое содержание работы: 1) Историческая справка;
2) Роль логарифмов в музыке;
3) Звезды, шум и логарифмы;
4) Логарифмическая спираль
5) Нотная грамота и язык логарифмов
Слайд 3
Немного истории
Известный шотландский математик, Джон Непер
вошел
в историю математики как изобретатель
логарифмов, он составитель первой
таблицы логарифмов, которой
посвятил 20 лет своей жизни.
“Описание удивительных таблиц
логарифмов” опубликовал
лишь в 1614 году.
Таблицы логарифмов
нашли немедленное применение.
Джон НЕПЕР
John Napier
(1550 - 1617)
Слайд 4
Немного истории
Параллельно с Непером над
составлением таблицы логарифмов работал другой любитель математики - Йост
Бюрги.
Бюрги составил таблицы логарифмов раньше, но только в 1620 году издал свою книгу "Таблицы арифметической и геометрической прогрессии с обстоятельным наставлением, как пользоваться ими при всякого рода вычислениях".
Йост Бюрги
(1552 - 1632)
Слайд 5
Немного истории
В 1623 г., т. е. всего
через 9 лет после издания
первых таблиц, английским математиком
Эдмундом
Гюнтером была изобретена первая логарифмическая
линейка, ставшая рабочим инструментом для многих
поколений вплоть до появления ЭВМ.
Слайд 6
Ода об экспоненте
Две шкалы Гунтера –
Вот чудо
изобретательности.
Экспонентой порождена
Логарифмическая линейка:
У инженера и астронома не было
Инструмента
полезнее, чем она.
Даже изящные искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых логарифмов?
Английский поэт Э.Брилл
Слайд 7
Логарифмы в музыке
«… Даже изящные искусства питаются ею
Разве музыкальная
гамма не есть -
Набор передовых логарифмов?»
Из «Оды экспоненте»
Слайд 8
«Товарищ мой по гимназии любил играть на рояле,
но не любил математику.
Он даже говорил с оттенком
пренебрежения, что музыка и математика несовместимы.
«Правда Пифагор нашел какие-то соотношения между звуковыми колебаниями, но ведь как раз пифагорова- то гамма для нашей музыки и оказалось неприемлемой»
Слайд 9
Частоту любого звука можно выразить
формулой
Ноте «до» соответствует частота, равная n колебаниям в секунду.
В
октаве частота колебаний нижнего звука в 2 раза меньше верхнего.
Тогда ноте «до» 1-й октавы будут соответствовать 2n колебания в секунду, а ноте «до» 3-й октавы – 3n колебания в секунду и т.д.
Обозначим все ноты хроматической гаммы номерами р.
Слайд 10
Логарифмируя эту формулу, получаем
Слайд 11
Принимая частоту самого низкого «до» за единицу n=1
и приводя логарифмы к основанию 2, имеем
Слайд 13
«Открылась бездна звезд полна. Звездам числа нет, бездне
– дна».
Звёзды
Во II веке до н.э.
Гиппарх разделил звезды на 6 групп. Самые яркие – звезды 1-ой величины, самые слабые – 6-ой величины.
Установлено, что звезда 1-ой вел. ярче звезды 6-ой вел. ровно в 6 раз.
Слайд 14
Громкость звука – 1 бел, 0,1 бел –
1 децибел.
Тихий шелест листьев – 1 бел.
Шумы
Слайд 18
Рев двигателя самолета – 20 бел
Слайд 19
Шум, громкость которого больше 8 бел – признана
вредной для организма человека.
Эта норма зачастую превосходится в школе,
на дискотеках, на заводах и фабриках.
Музыка: рок – 10-12 белов
Слайд 20
Последовательные степени громкости – 1 бел, 2 бел,
3 бела и т.д. составляют арифметическую прогрессию.
Физическая же «сила»
этих шумов (точнее - энергия) составляет геометрическую прогрессию со знаменателем 10.
Громкость – есть десятичный логарифм его физической силы
Итак, мы видим, что при оценке видимой яркости светил и при оценке громкости шума мы имеем дело c логарифмами.
Величина ощущения прямо пропорциональна логарифму величины раздражения.
Слайд 21
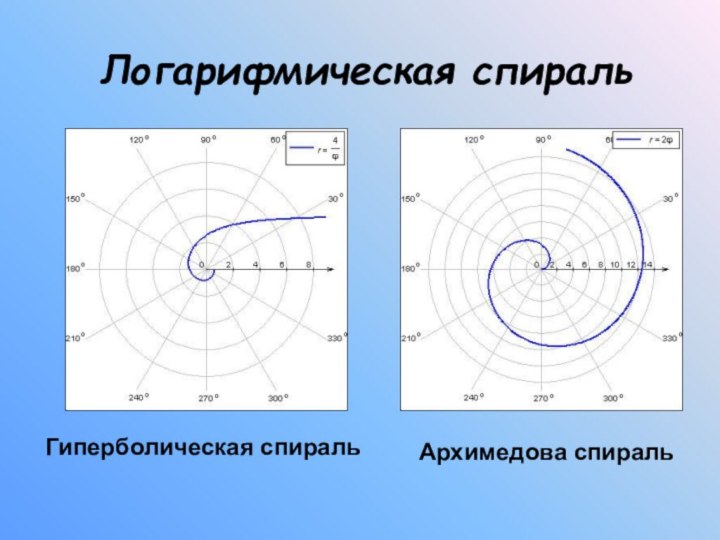
Логарифмическая спираль
Спираль – это плоская кривая линия, многократно
обходящая одну из точек на плоскости, которая называется полюсом
спирали.
Слайд 22
Первым ученым, открывшим эту удивительную кривую, был
французский
математик Рене Декарт
Рене Декарт
(1596-1650гг.)
Слайд 23
Логарифмическая спираль
Гиперболическая спираль
Архимедова спираль
Слайд 24
Логарифмическая спираль
является траекторией точки, которая движется вдоль
равномерно вращающейся
прямой, удаляясь от полюса
со скоростью,
пропорциональной
пройденному
расстоянию.
Т.е. в логарифмической спирали
углу поворота пропорционален
логарифм этого расстояния.
Слайд 25
Свойство логарифмической спирали
Якоб Бернулли открыл поразительное свойство спирали:
кривая с «твёрдым» характером.
Она не изменяется при сжатиях,
растяжениях и поворотах.
Слайд 26
По логарифмической спирали свёрнуты раковины
многих улиток и
моллюсков
Слайд 27
По логарифмическим спиралям выстраиваются
цветки в соцветиях подсолнечника
Слайд 28
Даже пауки, сплетая паутину, закручивают нити вокруг центра
по логарифмической спирали
Слайд 29
По логарифмическим спиралям выстраиваются
рога многих животных
Слайд 30
По логарифмической спирали формируется тело циклона
Слайд 31
По логарифмическим спиралям закручены многие галактики, в
частности Галактика, которой принадлежит Солнечная система
Слайд 32
Человеческое ухо – это маленькое чудо!
Улитка является органом,
воспринимающим звук, в котором самой природой заложена
ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ!
Улитка
Слайд 33
Траектории насекомых
летящих на свет также описывают логарифмическую
спираль.
**************************
Логарифмическая спираль единственная из спиралей не меняет своей
формы при увеличении размеров.
Видимо, это свойство и послужило причиной того, что в живой природе логарифмическая спираль встречается чаще других.
Слайд 34
Нотная грамота и язык логарифмов
Изгиб гитары желтой
Ты
обнимаешь нежно
Струна осколком эха,
Пронзит тугую высь
Качнётся купол неба,
Большой и
звёздно-снежный
Как здорово, что все мы здесь
Сегодня собрались
Слайд 36
Нотная грамота и язык логарифмов