Презентация на тему по алгебре по теме Повторение избранных тем 7-9 классов

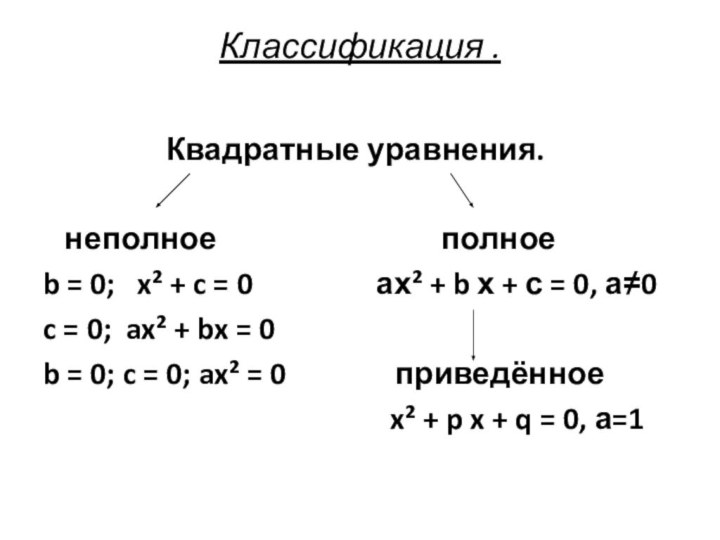
х₂, то квадратный трехчлен ax²+bx+c, раскладывается на множители следующим

образом:
ax²+bx+c= а·(х - х₁)(х - х₂).

Квадратные уравнения.

неполное

полное
b = 0; x² + c = 0 ах² + b х + с = 0, а≠0
c = 0; ax² + bx = 0
b = 0; c = 0; ax² = 0 приведённое
x² + p x + q = 0, а=1

2х² – 8 = 0 и

2) х² – х = 0
Решения: 2х² – 8 = 0 и х² – х = 0
2(х² - 4)=0 х(х-1)=0
2≠0; х² - 4 =0 х=0; х-1=0
х² = 4 х=0; х=1
х = ± 2

квадратного уравнения по формуле

D = b²- 4ac.
2) Дискриминант показывает сколько корней имеет уравнение
- если D<0, то данное квадратное уравнение не имеет корней;

уравнение имеет
единственный корень, который

равен           

- если D>0, то данное квадратное уравнение
имеет два корня, которые равны

х₁ и х₂ являются корнями приведённого

квадратного уравнения х² + px + q = 0 тогда и только тогда, когда х₁ + х₂ = - p, х₁ · х₂ = q.
Следствие: х² + px + q = (х – х₁)(х – х₂)

Например, x²-7x+10=0
методом подбора проверим числа 2 и 5. Их произведение равно 10 (т.е. свободному члену уравнения), а их сумма равна 7, (т.е. второму коэффициенту уравнения , но с противоположным знаком )
Ответ: 2 и 5

0
2) х² - 19х + 18 = 0
3)

х² + 9х + 20 = 0

0, т.е. а + в + с = 0

, то х₁ = 1 х₂ = с/а.
2) Если а –в + с = 0, то х₁ = -1 х₂ = -с/а.
3) Если а = с, в = а ² + 1, то
х₁ = –а = - с х₂ = -1/а = -1 /с.
4) Если а = с , в = - (а² + 1), то
х₁ = а = с х₂ = 1/а = 1/с

1 = 0,

2) 5х² - 4х – 9 = 0, 3) 6х² + 37х + 6 = 0,
4) 13х² - 18х + 5 = 0,
5) 7х² - 50х + 7 = 0,

2х – 3
Перенести все слагаемые с х влево, а

числа вправо,
меняя при этом знак на противоположный:

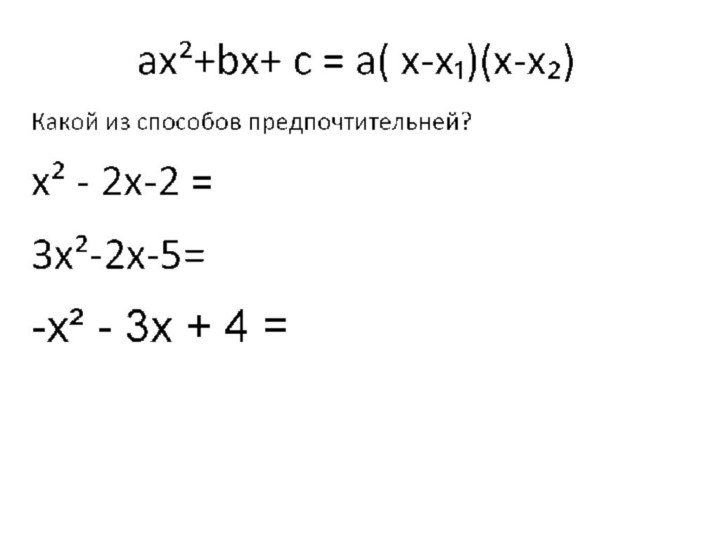
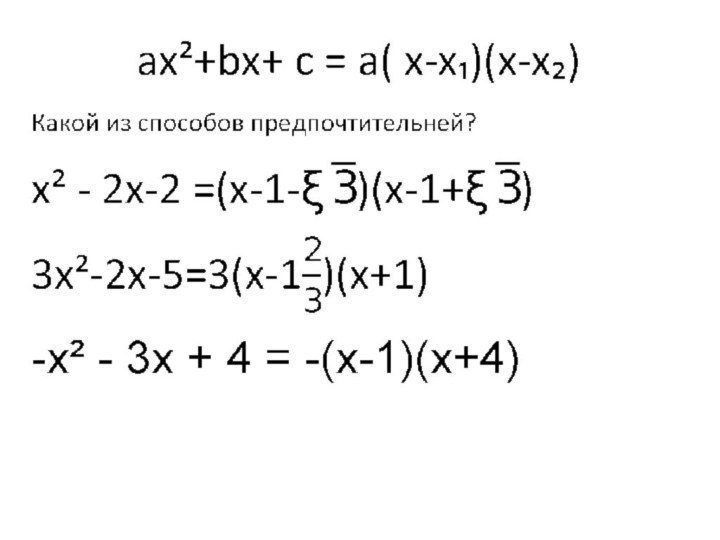
5х – 2х > - 3 + 15

Привести подобные слагаемые:

3х > 12

Разделить обе части неравенство на число,
стоящее перед х (если это число положительное,
то знак неравенства не меняется; если это число
отрицательное, то знак неравенства меняется
на противоположный):

3·х > 12 / (: 3)

х > 4

Перейти от аналитической модели к
геометрической модели:

х
4

Указать множество решений
неравенства, записав ответ:

Ответ: (4; +∞ )

.

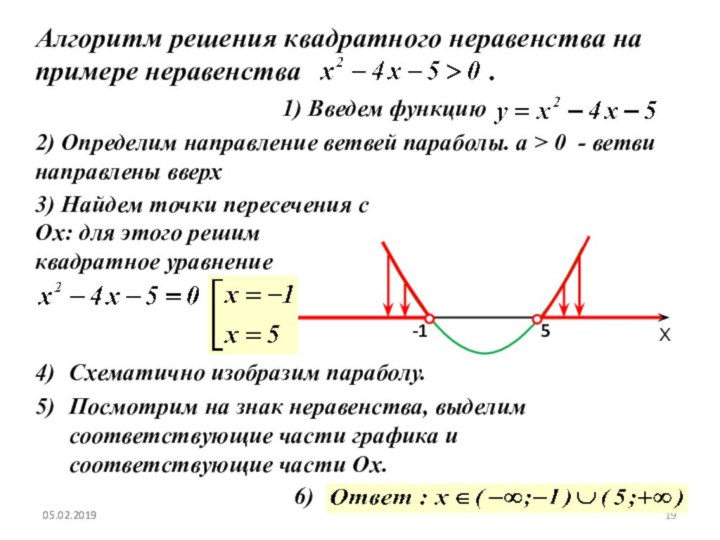
Х

5

-1

2) Определим направление ветвей параболы. а > 0 - ветви направлены вверх

1) Введем функцию

3) Найдем точки пересечения с Ох: для этого решим квадратное уравнение

4)

Схематично изобразим параболу.

5)

Посмотрим на знак неравенства, выделим соответствующие части графика и соответствующие части Ох.

6)