Презентация на тему по алгебре Производная

тьмой окутан.
Да будет свет! И вот

явился Ньютон.
А.Поуп.

Ковалева Ирина Константиновна

и другие вопросы мы сегодня и ответим.

Ковалева Ирина Константиновна

1666 года было необычным
Солнце нещадно палило, обжигая поля, дома

и дороги прямыми лучами.

Казалось, все вокруг замерло, оцепенело, подчиняясь жестокой силе солнца.

Не хватало воды. Только в одном Лондоне чума унесла около 100 тысяч человек.

В это тяжелое время , как ни парадоксально, и родилась
высшая математика, или, как говорят иногда,
анализ бесконечно малых, или еще – дифференциальное и
интегральное исчисление.

десятков математиков разных лет и стран, чтобы в виде

метода флюксий преподать человечеству дифференциальное и интегральное исчисление.

Ковалева Ирина Константиновна

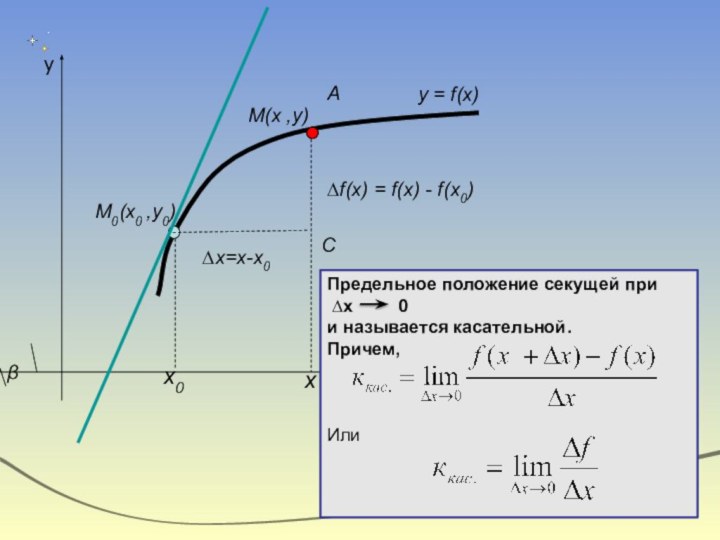
(флюэнтой Ньютон называл функцию,
флюксией – ее производную)

кинематики – рассчитать либо равномерное прямолинейное движение, либо равномерное

вращение вокруг оси.
А планеты на небосводе двигались по самым замысловатым кривым . Свести эти движения планет к простым древним учёным не удавалось.
Лишь в 17 веке немецкому учёному Иоганну Кеплеру удалось сформулировать законы движения планет. Оказалось, что планеты движутся по эллипсам, и притом неравномерно. Объяснить, почему это так, Кеплер не смог.

динамики, сформулировал закон всемирного тяготения и развил математические методы,

позволявшие сводить неравномерное к равномерному, неоднородное к однородному, криволинейное к прямолинейному.
В основе лежала простая идея – движение любого тела за малый промежуток времени можно приближённо рассматривать как прямолинейное и равномерное.
Одновременно с Ньютоном немецкий философ и математик Готфрид Вильгельм Лейбниц изучал, как проводить касательные к произвольным кривым.

сути дела тождественным построенному Ньютоном. Обозначения, введённые Лейбницем, оказались

настолько удачными, что сохранились и по сей день.
Новая математика Ньютона и Лейбница состояла из двух больших частей – дифференциального и интегрального исчислений.
В первом из них говорилось, как, изучая малую часть явления, сводить неравномерное к равномерному.
Во второй – как из малых равномерных частей конструировать сложное неравномерное явление.

исходя их вопросов
механики определения мгновенной скорости прямолинейного
неравномерного

движения.

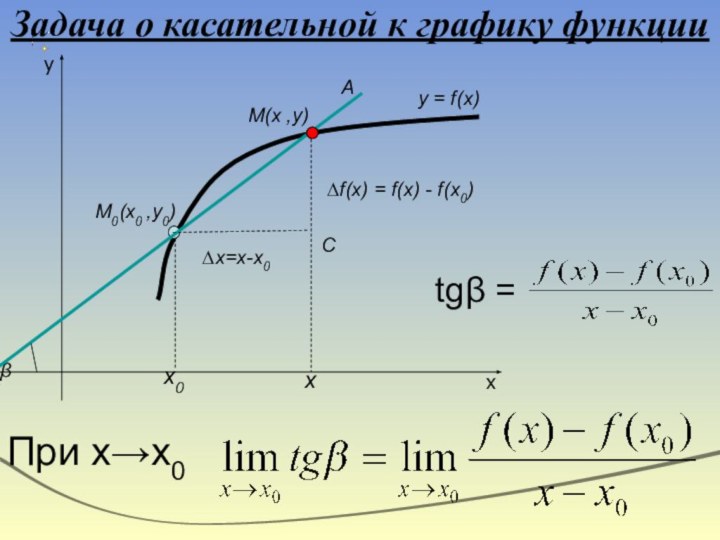
Попробуйте ответить на вопрос:
что такое скорость?

А мгновенная скорость?

«Фейнмановских лекций по физике»)
-Мадам, Вы нарушили правила уличного движения.

Вы ехали со скоростью 90 км в час.
-Простите, но это невозможно. Как я могла проехать 90 км за час, если я еду всего лишь 7 минут!
- Я имею в виду, мадам, что если бы продолжали ехать таким же образом, то через час Вы проехали 90 км.
-Если бы я продолжала ехать, как ехала , еще час, то налетела бы на стенку в конце улицы!.
-Ваш спидометр показывает 90 км/час.
-Мой спидометр давно сломан и не работает.

Как видите, полицейский не смог объяснить, что такое скорость 90 км/час. А вы смогли бы?

Именно над этим вопросом задумался Ньютон и…
открыл высшую математику.

по закону S(t).
Тогда за промежуток времени t точка проходит

расстояние S(t).
Пусть ∆t – малый промежуток времени. Путь, пройденный за время t+ ∆t, равен S(t+ ∆t ).
Тогда средняя скорость

Vср. Vмгн.
Значит,

, физик, философ.
Лейбниц – прямая противоположность И.Ньютону

то Лейбниц – философией и поэзией.
Если первый все-таки

прошел систематический курс обучения, то второй – скорее самоучка.
У Ньютона математика была орудием физики, а у Лейбница – орудием философии и логики.
Ньютон не разбрасывался в науке и творил в основном в области физики и математики,
Лейбниц же – личность разносторонняя, увлекающаяся: он был политиком, историком, юристом, дипломатом, философом и, наконец, математиком.
Один жил в Англии и не выезжал из нее,
Лейбниц – в Германии, но бывал во многих других странах Европы.

они подошли к открытию анализа бесконечно малых.
Но и тут

различия.
Первый подошел к открытию через понятие флюксий, решая задачу механики,
а второй – через дифференциал, решая задачу о касательной к кривой.

- f(x0)

∆х 0
и называется касательной.
Причем,

Или

- х0

(1)

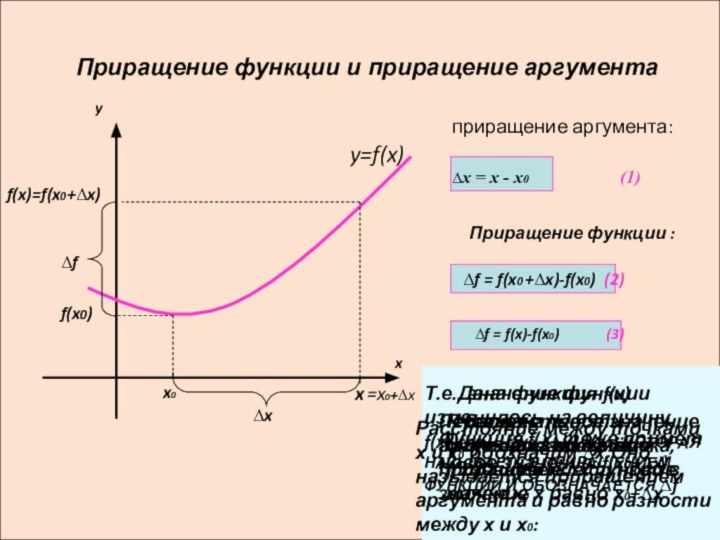
Приращение функции :

∆f = f(x0 +∆x)-f(x0) (2)

∆f = f(x)-f(x0) (3)

x

В окрестности точки х0 возьмём точку х

Пусть х0- фиксированная точка, f(х0)- значение функци в точке х0

Расстояние между точками х и х0 обозначим ∆х.Оно называется приращением аргумента и равно разности между х и х0:

Первоначальное значение аргумента получило приращение ∆х, и новое значение х равно х0+∆х

Функция f(х) тоже примет новое значение: f(x0+∆x)

Т.е., значение функции изменилось на величину f(x)-f(x0)= f(x0 +∆x)-f(x0),КОТОРАЯ НАЗЫВАЕТСЯ ПРИРАЩЕНИЕМ ФУНКЦИИ И ОБОЗНАЧАЕТСЯ ∆f

Дана функция f(x)

b), в точке х этого интервала называется предел отношения

приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

пришли к открытию дифференциального и интегрального исчислений.

V(t) = S’(t)

кривой в точке хо, равен значению производной в

этой точке.
К кас.= f’(хо )

q(t) количество электричества, протекающее через поперечное сечение проводника за

время t.
Пусть Δt – некоторый промежуток времени, Δq = q(t+Δt) – q(t) – количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δt. Тогда отношение называют средней силой тока.
Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, при условии, что Δt→0.

в воде за промежуток времени [t0;t1] (масса соли, растворившейся

в воде изменяется по закону х = f(t)) определяется по формуле .


Скорость растворения в данный момент времени

геометрических задач, задач из естественных и гуманитарных наук, экономических

задач оптимизационного характера.
И, конечно, не обойтись без производной при исследовании функции и построении графиков, решении уравнений и неравенств

«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И. Лобачевский

∆x = x – x0
2)

∆f = f(x+x0) – f(x0)
3)

4)