Презентация на тему Методы решения квадратного уравнения

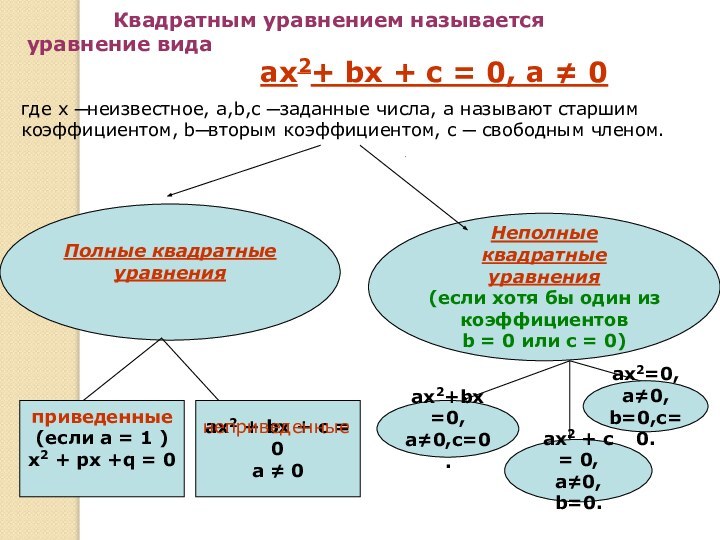
«Квадратные уравнения».


Рассмотреть несколько способов решения одной задачи и научиться

выбирать из них наиболее оригинальный , оптимальный.

Познакомиться с новыми приёмам устного решения квадратных уравнений.

тремя различными способами, чем решать три-четыре различные задачи.

Решая одну

задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.
У.У. Сойер

уравнением называется уравнение вида

ax2+ bx + c = 0, а ≠ 0

где х ─неизвестное, a,b,c ─заданные числа, а называют старшим коэффициентом, b─вторым коэффициентом, c ─ свободным членом.

Неполные квадратные уравнения
(если хотя бы один из коэффициентов
b = 0 или c = 0)

Полные квадратные уравнения

приведенные
(если а = 1 )
х2 + px +q = 0

ax2 + bx + c = 0
а ≠ 0

неприведенные

ax2 + c = 0,
a≠0, b=0.

ax2=0,a≠0,
b=0,c=0.

ax2+bx=0,
a≠0,c=0.

= 0

2) х² - 9х = 0
3) 4х + х² - 1 = 0 4) 2х – 5 = 0
5) 0,3 - 0,2х - х² = 0 6) 5х² = 0
7) -7х + х - 0,5 = 0 8) 49х² = 0

Какое из этих уравнений не является квадратным?

Назовите неполные квадратные уравнения.

Назовите приведенные квадратные уравнения.

Какие уравнения можно решить по формуле корней квадратного уравнения?

Какие уравнения можно решить разложением на множители, выделением квадрата двучлена, извлечением квадратного корня?

1. 3х2−х = 0,

Б: 1. х2 −7х +1=0,
2. х2 −25 = 0, 2. 7х2 − 4х +8 = 0,
3. 4х2 + х −3 = 0, 3. х2 + 4х −4 = 0,
4. 4х2 = 0. 4. х2 −5х −3 = 0.

Не решая уравнение
х2 −8х + 7 = 0.
Найдите:
а) сумму корней:
б) произведение корней:
в) корни данного уравнения:

то

х1,2= -

D>0,
то х1=

х2=

Первый
способ( по общей формуле):

С 1591 г. мы пользуемся формулами при решении квадратных уравнений

3. 2х2-3х+2=0,
4. 4х2-12х+9=0.

х1= ½, х2=2.
решений нет.
х1=1,5, х2=1,5.

корни можно найти по теореме, обратной теореме Виета:

х1+х2=-p,
х1∙х2=q.

Например,
уравнение х2-3х+2=0
имеет корни х1=2, х2=1
так как х1+х2=3, х1∙х2=2.

Второй способ( по т., обратной теореме Виета):

обратной теореме Виета.
х2+10х+9=0,
х2+7х+12=0,
х2-10х-24=0.
х1=-9,х2=-1.
х1=-4,х2=-3.
х1=12,х2=-2.

Третий способ( формула корней приведенного квадратного уравнения):
Задание 3: Решите

квадратные уравнения по данной формуле:

х2-10х-24=0,
х2-16х+60=0

Этот способ применяют, когда можно легко найти корни уравнения,

используя теорему Виета и, что самое важное, когда дискриминант - точный квадрат.

Например: Решим уравнение 2х2-11х+15=0.
«Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение: у2-11у+30=0.
По теореме, обратной теореме Виета у1= 5,у2= 6. тогда х1=у1/2, х2=у2/2; т.е. х1=2,5 , х2=3.

Четвёртый способ( способ « переброски»):

Ответ :

Решаем, используя метод «переброски»

Получим уравнение

Делим числа 9 и ( -2) на 6:

10х2-11х+3=0,
3. 3х2+11х+6=0
х1=1,5 , х2=3.
х1=0,5 ,х2=0,6.
х1=-3,х2=- .

а≠0.

1.Если а+в+с=0(т.е.сумма коэффициентов
уравнения равна нулю), то х1=1,х2=с/а.
Например: 345х2-137х-208=0 (345-137-208=0), значит,
х1= 1,х2= - 208/345.
2.Если а-в+с=0 (или в=а+с), то х1=-1,х2= - с/а.
Например, 313х2+326х+13=0 (326=313+13), значит
х1=-1,х2=-13/313.

Пятый способ: « Способ коэффициентов»

11х2+27х+16=0;
5. 939х2+978х+39=0.
Задание 4: Решите квадратные уравнения методом «коэффициентов»:

х1=1,х2=

.
х1=1,х2=- .
х1=1,х2=- .
х1=-1,х2=- .
х1=-1,х2=- .

теореме, обратной теореме Виета;
По формуле для нахождения корней приведенного

квадратного уравнения;
Способом « переброса»;
Способом коэффициентов.