- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему: Различные виды решения квадратных уравнений.
Содержание
- 2. Цель урока: формирование представления о возможности решения квадратных уравнений различными способами.
- 3. Проблема: 1. Изменится ли способ решения квадратного уравнения
- 4. Ход урока 1.Орг.момент.Математическая зарядка. 2.Повторение и обобщение изученного
- 5. Математическая зарядкаВерный ответ - руки вверх ,
- 6. 2.Повторение и обобщение изученного материала.
- 7. 1)Универсальная формула.
- 8. Пример:6x2 + x – 2 = 0D
- 9. 2) Формула для четного коэффициента
- 10. Пример: 3x2 – 4x
- 11. 3) Приведенное квадратное уравнение (Старший коэффициент равен
- 12. Пример:x2 – 14x – 15 = 0x1 = 15, x2 = -1
- 13. 4) Теорема Виета.Чтобы числа x1 и x2
- 14. 5)Теорема, обратная теореме Виета. Если числа
- 15. 6) Разложение левой части уравнения на множители.
- 16. 7) Метод выделения полного квадрата● Пример
- 17. 8). Графическое решение квадратного уравнения Если
- 18. Пример:.Решим графически уравнение х2 –
- 19. Новые способы решений квадратных уравнений 9) Решение
- 20. Пример : Решим уравнение 2х2 – 11х
- 21. 10). Решение квадратных уравнений с помощью циркуля
- 22. Пример:
- 24. Решение квадратного уравнения ax2+bx+c=0 в зависимости от
- 25. 2) Если a – b –
- 26. 3) Если a = c =
- 27. 4) Если a = c =
- 28. 5) Если ax2 + (a2-1)x –
- 29. 6) Если ax2 – (a2-1)x –
- 30. Дом.задание:Используя 1-6 способы решения кв.уравнений в зависимости от соотношений между коэффициентами ,составить уравнения и решить их.
- 31. Вывод: все рассмотренные способы решения квадратных уравнений
- 32. Скачать презентацию
- 33. Похожие презентации
Цель урока: формирование представления о возможности решения квадратных уравнений различными способами.






























Слайд 2
Цель урока:
формирование представления о возможности решения квадратных
уравнений различными способами.
Слайд 3
Проблема:
1. Изменится ли способ решения квадратного уравнения в
зависимости от его вида?
2.Можно ли одно и тоже
уравнение решить не единственным способом?
Слайд 4
Ход урока
1.Орг.момент.Математическая зарядка.
2.Повторение и обобщение изученного материала.
3.Лекция(сообщения учащихся о рассмотренном способе решения с примером применения
данного способа).4.Дом.задание
5.Итог урока , выводы
Слайд 5
Математическая зарядка
Верный ответ - руки вверх , неверный
- руки вперед
(наклоны вправо – влево и т.д.)
Предлагаются
задания для устного счета с ответом(верным или неверным).Ученики, обдумывая , «сигналят» об ответе .
Слайд 7
1)Универсальная формула.
ах2 + bx + c=0
D = b2 - 4acD>0 D=0 D<0
X1,2 = X = Действ. корней нет
Слайд 9
2) Формула для четного коэффициента b.
ах2 + bx + c = 0
b = 2m
D1 = m2 - ac
D1>0 D1 = 0 D1<0
Действительных
корней нет
Слайд 11
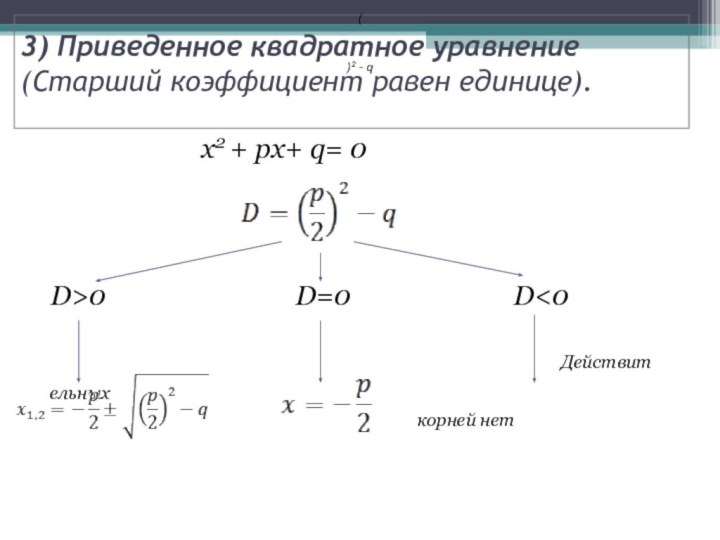
3) Приведенное квадратное уравнение
(Старший коэффициент равен единице).
х2 + px+ q= 0
D>0 D=0 D<0
Действительных
корней нет
(
)2 - q
Слайд 13
4) Теорема Виета.
Чтобы числа x1 и x2 являлись
корнями уравнения:
ax² + bx + c = 0
необходимо
и достаточно выполнения равенстваx1 + x2 = -b/a и x1x2 = c/a
Теорема Виета позволяет судить о знаках и абсолютной величине квадратного уравнения, а именно:
x² + bx + c = 0
Если b>0, c>0 то оба корня отрицательны.
Если b<0, c>0 то оба корня положительны.
Если b>0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине больше положительного.
Если b<0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине меньше положительного.
Слайд 14
5)Теорема, обратная теореме Виета.
Если числа p, q, x1,
x2 таковы, что х1 + х2= -p, x1 ∙
x2 = q , то х1 и х2 – корни уравненияx2 + px + q = 0 .
Пример: x2 - 7x + 12 = 0
x1 + x2 = 7 x1 = 3,
x1 ∙ x2 = 12 x2 = 4
Слайд 15
6) Разложение левой части уравнения на множители.
Решим
уравнение х2 + 10х – 24 = 0. Решение:
Разложим левую часть уравнения на множители: х2 + 10х – 24 = х2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2). Следовательно, уравнение можно переписать так: (х + 12)(х – 2) = 0. Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = - 12. это означает, что числа 2 и – 12 являются корнями уравнения х2 + 10х – 24 =0.
Слайд 16
7) Метод выделения полного квадрата●
Пример
Решим уравнение х2 + 6х
– 7 = 0 Выделим в левой части полный квадрат. Для этого запишем выражение х2 + 6х в следующем виде: х2 + 6х = х2 + 2· х ·3. В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3. поэтому чтобы получить полный квадрат, нужно прибавить 32, так как х2 + 2· х ·3 + 32 = (х + 3)2 . Преобразуем теперь левую часть уравнения х2 + 6х – 7 = 0, прибавляя к ней и вычитая 32. Имеем: х2 + 6х – 7 = х2 + 2· х ·3 + 32 – 32 – 7 = (х + 3)2 – 9 – 7 = (х + 3)2 – 16. Таким образом, данное уравнение можно записать так: (х + 3)2 –16 = 0, т.е. (х + 3)2 = 16. Следовательно, х = 3 = 4, х1 = 1, или х +3 = - 4 , х2 = – 7.
Слайд 17
8). Графическое решение квадратного уравнения
Если в уравнении
x2 + px + q
= 0 перенести второй и третий члены в правую часть, то получим x2 = – px – q . Построим графики зависимостей у = х2 и у = – px – q . График первой зависимости – парабола, проходящая через начало координат. График второй зависимости – прямая. Возможны следующие случаи: прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения; - прямая и парабола могут касаться (только одна общая точка),т.е. уравнение имеет одно решение; - прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.Слайд 18 Пример:.Решим графически уравнение х2 – 3х –
4 = 0. Решение. Запишем уравнение в
виде х2 = 3х + 4 Построим параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N (3;13). Прямая и парабола пересекаются в двух точках А и B с абсциссами х1 = – 1 и х2 = 4.Слайд 19 Новые способы решений квадратных уравнений 9) Решение уравнений способом
«переброски»
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2 х2 + а bх + ас = 0.
Пусть ах = у, откуда х =y/a ; тогда приходим к уравнению
у2 + by + ас = 0,
равносильного данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = у1 /a и х2 = у2 /a . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.Слайд 20 Пример : Решим уравнение 2х2 – 11х +
15 = 0. Решение. «Перебросим» коэффициент 2 к свободному члену,
в результате получим уравнение у2 – 11y +30 = 0. Согласно теореме Виета
Слайд 21 10). Решение квадратных уравнений с помощью циркуля и
линейки.
Графический способ решения квадратных уравнений с помощью
параболы неудобен. Если строить параболу по точкам, то потребуется много времени, и при этом степень точности получаемых результатов невелика.Предлагаем следующий способ нахождения корней квадратного
уравнения
ах2 + bх + с = 0
с помощью циркуля и линейки.
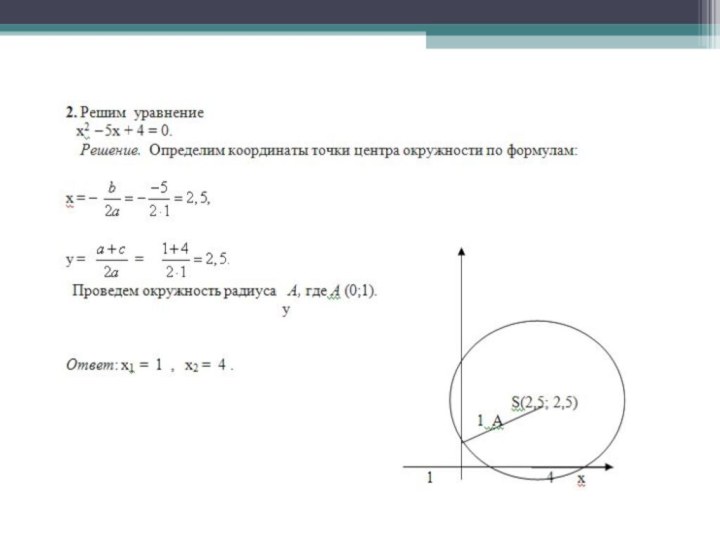
Допустим, что искомая окружность пересекает ось абсцисс в
точках B (х1 ;0) и D (х2 ;0), где х1 и х2 – корни уравнения
ах2 + bх + с = 0, и проходит через точки А (0;1) и С (0; ) на
оси ординат. Тогда по теореме о секущих имеем ОВ∙ОD = ОА ∙ ОС, откуда
ОС = (ОВ∙ОD) : ОА=( х1 ∙ х2 ):1= с/а
.
Слайд 24 Решение квадратного уравнения ax2+bx+c=0 в зависимости от соотношения
между коэффициентами a,b,c.
1) Если a+ b+ c =
0, то x1 = 1, x2 = c/a .
Пример: 2x2 + 3x – 5 =0
2+3-5=0, значит
x1 = 1; x2 = -5/2
Слайд 25 2) Если a – b – c
= 0, то x1 = -1;
x2 = -c/a.
Пример:
2x2 + 3x - 1=02-3+1=0, значит
x1 = -1; x2 = 1/2
Слайд 26 3) Если a = c = n,
b = n2 + 1, т. е. nx2 +
(n2+1)x +n=0, то x1 = -n; x2 = -1/n Пример: 2x2 + 5x + 2=0
5=22+1, n=2
x1 = -2; x2 = -1/2
Слайд 27 4) Если a = c = n,
b = -(n2+1), т. е. nx2 – (n2+1)x+n=0, то
x1 = n; x2 = 1/n Пример: 3x2 – 10x + 3=0
3х2-(32+1)х+3=0
x1 = 3; x2 = 1/3
Слайд 28 5) Если ax2 + (a2-1)x – a
= 0, то
х= -а; x = 1/a
Пример: 5x2
+ (52-1)x – 5 = 0 х=-5, x = 1/5
Слайд 29 6) Если ax2 – (a2-1)x – a
= 0, то х=а , x = -1/a
Пример:
5x2 – (52-1)x – 5 = 0 х=5, x = -1/5