Слайд 2
Специальность: математика
Педагогический стаж: 23года
Присвоена квалификация: учитель математики
Категория:
первая c 2001 года
Стаж работы в МБОУ «Школа №169:
1 год
Награды:
Почетная грамота Администрации Автозаводского р-на г.Нижнего Новгорода Управление образования и социально-правовой защиты детства, 2006г.,2007г.
Почетная грамота Департамент образования и социально-правовой защиты детства Администрации г.Нижнего Новгорода, 2007г.
Благодарственное письмо Администрации МОУ средней образовательной школы №6 г. Нижнего Новгорода, 2009г.
Образование: Ульяновский ордена «Знак Почета» госпединститут им. И.Н. Ульянова, математический факультет, 1988 г
Зенкина О.Г.
Слайд 3
Содержание
Используемые методы, приемы, формы
организации деятельности
Ожидаемые результаты
освоения раздела программы
Психолого-педагогическое обоснование
Цели, задачи раздела
Пояснительная записка
Поурочное
планирование по разделу
Методическая разработка урока
Самостоятельные и контрольная работы
Результаты выполнения
самостоятельных и контрольных работ
Список литературы
Слайд 4
Пояснительная записка
Учебная программа базового курса «Алгебра» для 7

класса вторая ступень обучения средней общеобразовательной школы составлена на
основе федерального компонента государственного общеобразовательного стандарта базового уровня общего образования.
Программа «Алгебра 7-9» под редакцией Зубаревой И.И.
«Книга природы написана на математическом языке и ее буквы - математические знаки и геометрические фигуры. А функция является тем средством математического языка, которое позволяет описывать процессы, движения, изменения, присущие природе».
Г.Галилей
Тема «Линейная функция» занимает второе место в содержании программы. На первом месте находится тема «Математический язык Математическая модель», в которой, повторяя материал курса математики 5-6 классов, вводятся новые термины: математический язык, математическая модель, а также понятие о трех этапах математического моделирования. У учащихся сформированы умения применять знания о математическом моделировании на практике для решения задач.
Слайд 5
Актуальность выбранной темы
Математические модели напрямую связаны с функциями,
потому функции становятся ведущей идеей курса алгебры практически во
всех разделах.
В концепции изучения функции по программе А.Г.Мордковича реализуется принцип: приоритетность функционально- графической линии.
Слайд 6
Цель раздела
Формирование представления о числовой функции на примере
линейной функции.
Слайд 7
Задачи раздела
Учебные
Развивающие
Воспитательные
Слайд 8
Психолого-педагогическое обоснование
Семиклассник
Характеризуется
Рост познава-тельной
активности и
любозна-тельности
Способность
к самостоя-тельному творческому
мышлению,
рассуждению,
сравнению, обобщению
Развитие
познава-тельных
интересов
Развитие
смысловой
логической памяти,
понятийного
мышления
Развитие
самосозна-
ния
и самооценки
Слайд 9
Ожидаемые результаты освоения раздела программы
Описывать свойства функции на
основе ее графического представления
Использовать функционально-графические представления для описания и
анализа учебных математических задач и реальных зависимостей
Использовать различные языки математики
Вычислять значения функций, заданных формулами, составлять таблицы значений функций
Строить по точкам графики функций
y=kx, y=kx+m
Слайд 10
Формы организации деятельности
Индивидуальная работа
Работа в парах
Групповая работа
Формы организации
деятельности
Фронтальная работа
Слайд 11
Методы обучения
словесные;
наглядные;
практические;
активные;
индуктивные и дедуктивные
Формы контроля: тесты,
самостоятельные и контрольные работы.
Слайд 12
Образовательные технологии
взаимоконтроль;
дидактическая игра;
проблемное изучение материала;
информационно-компьютерные технологии;
пары
и группы сменного состава;
самооценка;
тест с закрытыми ответами;
тихий и
устный опрос у доски.
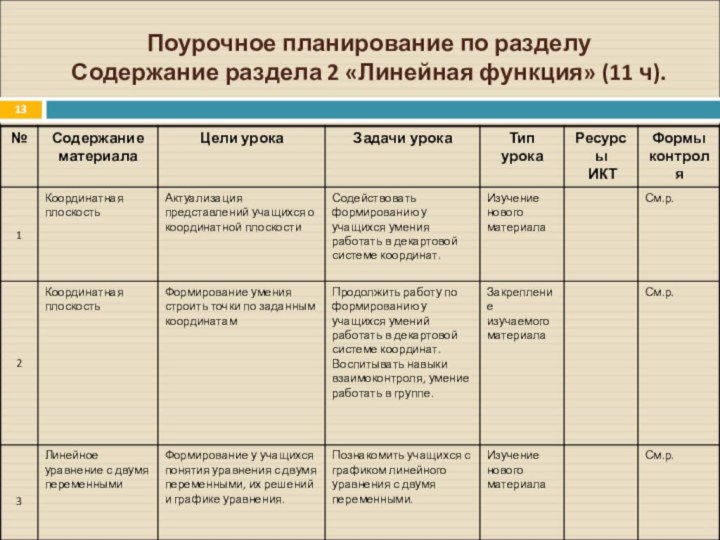
Слайд 13
Поурочное планирование по разделу
Содержание раздела 2 «Линейная функция»
(11 ч).
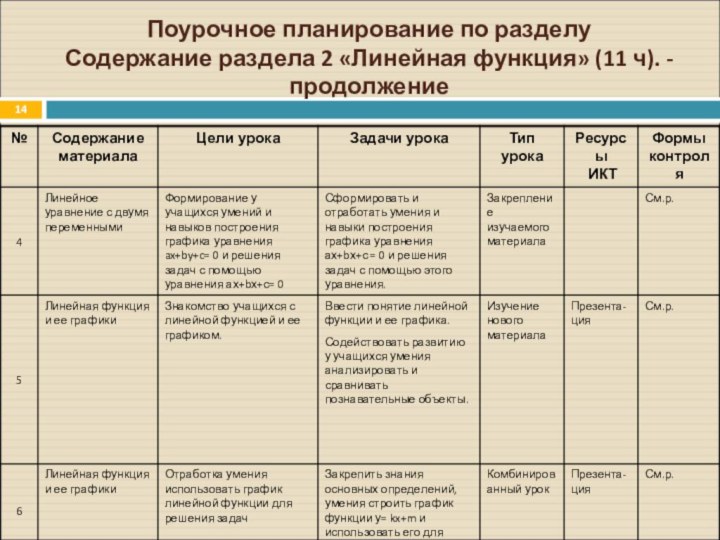
Слайд 14
Поурочное планирование по разделу
Содержание раздела 2 «Линейная функция»
(11 ч). - продолжение
Слайд 15
Поурочное планирование по разделу
Содержание раздела 2 «Линейная функция»
(11 ч). - продолжение
Слайд 16
Поурочное планирование по разделу
Содержание раздела 2 «Линейная функция»
(11 ч). - продолжение
Слайд 17
Методическая разработка урока
«Линейная функция и ее график»
Тип урока
Урок
изучения нового материала.
Цель урока
Знакомство учащихся с линейной функцией
и ее графиком.
Оборудование
Учебник, задачник.
Наглядное пособие: плакат «Линейная функция и ее график».
Компьютер.
Проектор.
Электронное сопровождение курса-7 (диск).
Карточки.
Слайд 18
Задачи урока
Развивающие
Воспитательные
Способствовать развитию умения анализировать, сравнивать познавательные объекты,
выделять главное в источнике информации; способствовать развитию мышления, памяти,
внимания.
Способствовать воспитанию аккуратности при выполнении построений; содействовать воспитанию стремления к активной познавательной деятельности; содействовать воспитанию коммуникативных навыков
Слайд 19
Структура урока
Организационный этап –2 мин.
Обеспечивается нормальная внешняя обстановка для работы на уроке, психологически
осуществляется подготовка учащихся к общению и предстоящему занятию. Мотивация учебной деятельности. Сообщается план урока.
Этап подготовки учащихся и активному сознательному усвоению знаний –5 мин.
Формируется целенаправленный характер учебной деятельности ,происходит актуализация опорных знаний, сообщается тема урока и формулируются задачи урока.
Этап усвоения новых знаний –20 мин.
Дается представление о линейной функции и ее графике, вырабатываются умения строить графики. Реализуется образовательная задача урока.
Этап закрепления знаний –15 мин.
Происходит закрепление и осмысление изученного материала.
Этап информации учащихся о домашнем задании и инструкции по его выполнению –3 мин.
Домашнее задание: § 8, № 4(в), 11(в), 14(в), 18(в) / № 52(б), 55(б).
Слайд 20
С какими новыми понятиями вы познакомились на предыдущем
уроке?
Дайте определение.
Что такое решение уравнения?
Сколько решений имеет линейное уравнение
с двумя переменными?
Что является графиком уравнения ax+by+c = 0?
Как выглядит график линейного уравнения?
Как построить график линейного уравнения с двумя переменными?
Слайд 21
Задание
Рассмотрим уравнение 3х-2у+6 = 0,
Выразите у из
этого уравнения: у = х+3,
Придавая х конкретные значения, легко
вычислить соответствующие значения у, например,
х=0, у=3.
х=-2, у=0.
Выразите у через х из уравнений и найдите точки, удовлетворяющие каждому уравнению:
а) 5х-2у = 0,
б) 3х+2у-16 = 0
Работа с учебником.
Рассмотрим теперь указанные преобразования в общем виде и сделаем выводы (работа с учебником стр. 43).
Слайд 22
График линейной функции
График линейной функции
y = kx
Графиком линейной функции y = kx является прямая, проходящая
через начало координат.
Коэффициент k называется угловым коэффициентом этой прямой.
При положительных k этот угол острый, при отрицательных - тупой.
График линейной функции
y = kx+b
Графиком линейной функции y = kx + b является прямая, смещенная на b единиц. Для построения графика достаточно двух точек.
Например: A(0;b) B(−kb;0), если k не равно 0.
Слайд 23
Линейная функция (определение)
Функция вида y = kx +b,
где k и b числа, а x
и y переменные, называется линейной функцией.
x – независимая переменная (аргумент)
y – зависимая переменная (функция)
Слайд 24
Линейная функция
Выбрав значение х (аргумента), можно легко вычислить
значение y (функции)
у = 2 х + 3
х =
у
= 2 · + 3
х
0
= 0 + 3 = 3
(0 ; 3)
х =
у = 2 · + 3
2
х
= 4 + 3 = 7
(2 ;7)
Слайд 25
Совет:
Если коэффициент k положительный,
выбирай положительное значение аргумента;
если
отрицательный - отрицательное
Слайд 26
Графиком линейной функции y = kx + b
является прямая линия.
y = 3x + 1
-5
-2
1
4
7
Слайд 27
Через две точки можно провести только одну прямую
линию
Для построения графика линейной функции достаточно двух точек!
Линейная функция
Слайд 28
Линейная функция
у = -2х +1
0
-2
1
5
Слайд 30
Коэффициент k
называют
угловым коэффициентом.
Чем больше угловой коэффициент
k, тем больше угол, образованный графиком функции с осью
ОХ
Полезно знать
Слайд 31
y= 0,5х +2
y= 4х +2
y= х +2
0
2
4
4
0
2
1
6
0
2
3
5
k =
0,5
k = 4
k = 1
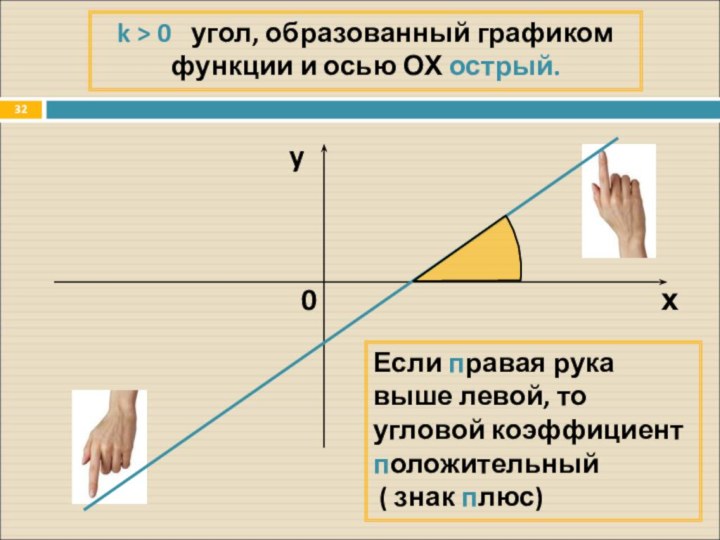
Слайд 32
х
y
Если правая рука выше левой, то угловой коэффициент
положительный
( знак плюс)
0
k > 0 угол,
образованный графиком функции и осью ОХ острый.
Слайд 33
k < 0 угол, образованный графиком функции
и осью ОХ тупой.
х
y
Если левая рука выше правой, то
угловой коэффициент отрицательный (знак минус)
0
Слайд 34
k = 0 - график параллелен оси ОХ
х
y
0
k
Слайд 35
Построим несколько графиков линейных функций, у которых одинаковые
угловые коэффициенты.
Если у линейных функций угловой коэффициент одинаковый, то
их графики параллельны!
Линейная функция
Слайд 36
у = -х + 4
у = -х
у
= -х - 5
0
4
-2
6
0
0
-3
3
0
-5
-6
1
Линейная функция
Слайд 37
у = -3х + 4
у = х +
4
у = 2х + 4
0
4
-1
7
0
4
2
6
0
4
1
6
4
Линейная функция
Слайд 38
График линейной функции пересекает ось OY в точке
(0;b).
Линейная функция
х =0 , y = k · x
+ b = k ·0 + b = 0 + b = b
Слайд 39
Закрепление новых знаний
Решение задач из учебника:
а) устно: №1 – 3. б) письменно: № 4(а), 11(а), 14(а), 18(а). в) самостоятельная работа: № 4(б), 11(б), 18(б).
Выполнение творческого задания: построить график функции:
Слайд 40
Итоги урока
С какими новыми понятиями познакомились?
Какая
функция называется линейной? Приведите примеры.
Что является графиком линейной функции?
Как можно построить график такой функции?
Достигли мы цели урока? Почему вы так считаете?
Информация о домашнем задании.
Запишите домашнее задание:
§ 8, № 4(в), 11(в), 14(в), 18(в) / № 52(б), 55(б).
Слайд 41
Самостоятельная работа-1
Тема «Координатная плоскость»
Вариант 1
1.
а) Постройте
по две точки в первой и третьей координатных четвертях
и запишите их координаты.
б) В каких координатных четвертях расположены точки: А(-23;28), В(67; -93)?
2. По координатам вершин постройте четырехугольник АВСD, А(2;3), В(-2;2),С(-3; -1), D(1,0).
3. Постройте прямую, удовлетворяющую уравнению х=2.
Вариант 2
1.
а) Постройте по две точки во второй и четвертой координатных четвертях и запишите их координаты.
б) В каких координатных четвертях расположены точки: С(58;34), D(-14; -15)?
2. По координатам вершин постройте четырехугольник АВСD, А(1;4), В(-2;0) С(1; -4), D(4;0).
3. Постройте прямую, удовлетворяющую уравнению y= -3.
Слайд 42
Самостоятельная работа-2
Тема «Линейная функция-1»
Вариант 1
1. Преобразуйте линейное
уравнение с двумя переменными -4х + 2у =6 к
виду линейной функции у = kх + m.
2. Постройте график полученной в п. 1 линейной функции. По графику определите:
а) координаты точек пересечения графика с осями координат;
б) значения функции при х = -2; -1; 2;
в) значения аргумента, если у = -3; 1; 4.
Вариант 2
1. Преобразуйте линейное уравнение с двумя переменными 6х - 3у =3 к виду линейной функции у = kх + m.
2. Постройте график полученной в п. 1 линейной функции. По графику определите:
а) координаты точек пересечения графика с осями координат;
б) значения функции при х = -2; -1; 2;
в) значения аргумента, если у = -3; 1; 4.
Слайд 43
Самостоятельная работа-3
Тема «Линейная функция-2»
Вариант 1.
Постройте график функции
у = 2х + 4 и с его помощью
найдите:
а) координаты точек пересечения графика с осями координат;
б) значения аргумента, при которых функция принимает отрицательные значения;
в) значения аргумента, при которых функция принимает положительные значения;
г) наибольшее и наименьшее значения функции на отрезке [-3; -1].
Вариант 2.
Постройте график функции у = -х – 2 и с его помощью найдите:
а) координаты точек пересечения графика с осями координат;
б) значения аргумента, при которых функция принимает отрицательные значения;
в) значения аргумента, при которых функция принимает положительные значения;
г) наибольшее и наименьшее значения функции на отрезке [-3; -1].
Слайд 44
Самостоятельная работа-4
Тема «Линейная функция у = kх»
Вариант 1.
1.
Постройте график прямой пропорциональности у =3х. Найдите по графику:
а)
значение функции при х = -2; 1; 1,5;
б) значение аргумента при у = -3; 6; 0;
в) наибольшее и наименьшее значение функции на луче [1; +∞).
2.а) Задайте прямую пропорциональность формулой, если известно, что ее график проходит через точку А(3;15);
б) Приведите пример линейной функции, график которой параллелен графику полученной функции.
Вариант 2.
1. Постройте график прямой пропорциональности у = -2х. Найдите по графику:
а) значение функции при х = -2; 1; 1,5;
б) значение аргумента при у = -4; 1; 2;
в) наибольшее и наименьшее значение функции на луче (-∞; -2).
2.а) Задайте прямую пропорциональность формулой, если известно, что ее график проходит через точку А(-4; -12);
б) Приведите пример линейной функции, график которой параллелен графику полученной функции.
Слайд 45
Контрольная работа по теме
«Линейная функция»
Вариант 1.
1.Функция

задана формулой у=2х+3. Принадлежат ли графику функции точки А(1;5)
и В(-1;-1)?
2.Постройте график функции у= -4х+3 и укажите координаты точек пересечения графика с осями координат.
3.Постройте график зависимости у=kx, если он проходит через точку А(-2;4). Найдите угловой коэффициент k.
4.При каком значении параметра а графики функций у=3х – 2 и
у= 7+(а – 2)х параллельны?
5.Найдите точку пересечения графиков функций у=3 и у= 2х – 1.
6.Постройте график уравнения │х+1│=2.
Вариант 2.
1.Функция задана формулой у= -2х+5. Принадлежат ли графику функции точки А(1;3) и В(-1;6)?
2.Постройте график функции у= 3х+4 и укажите координаты точек пересечения графика с осями координат.
3.Постройте график зависимости у=kx, если он проходит через точку А(2;-6). Найдите угловой коэффициент k.
4.При каком значении параметра а графики функций у=5х + 3 и у= -4+(а + 3)х параллельны?
5.Найдите точку пересечения графиков функций у=-1 и у= 3х+2.
6.Постройте график уравнения
│х-2│=1.
Слайд 46
Результаты выполнения
самостоятельных и контрольных работ
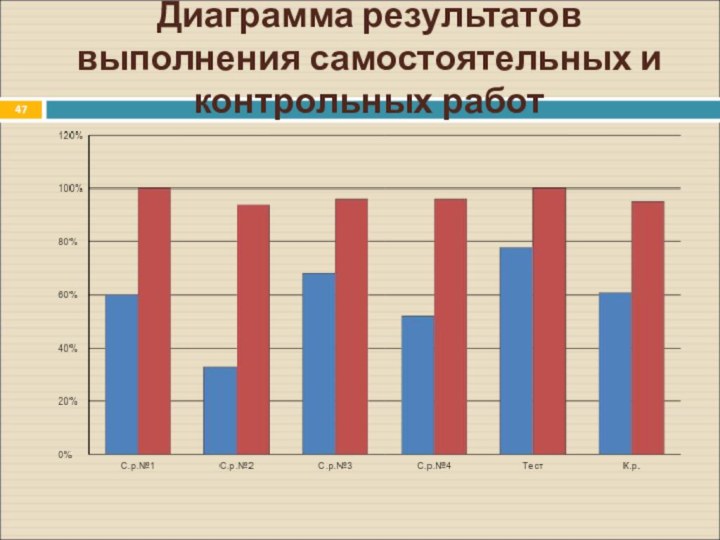
Слайд 47
Диаграмма результатов выполнения самостоятельных и контрольных работ
Слайд 48
Список литературы
Бурмистрова Т.А. Программы образовательных учреждений.: Алгебра 7-9
– М: Просвещение,2008.
Зубарева И.И. Программы: Алгебра 7-9 – М:
Мнемозина, 2009.
Кузнецов А.А. Примерные программы второго поколения – М: Просвещение, 2009.
Колеченко А.К. Энциклопедия педагогических технологий – изд. КАРО, С-Петербург, 2002.
Конаржевский Ю.А. Анализ урока – М: Центр «Педагогический поиск», 2000.
Голубева Л.В. Анализ урока – Волгоград: Учитель, 2007.
Григорьева Г.И. Нестандартные уроки по алгебре 7-9 кл. – Волгоград: ООО «Экстремум»,2006.
Глейзер Г.И. История математики в школе 5-7 классы – М: Просвещение,1981.
w.w.w.niro.nnov.ru
w.w.w.apkpro.ru
fppk.sckools.perm.ru