Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по алгебре на тему Одночлен 7 класс

Содержание

«Я слышу-я забываю, я вижу- я запоминаю, я делаю- я понимаю» (Китайская мудрость)Девиз урока:
«Я слышу-я забываю, я вижу- я запоминаю, я делаю- я понимаю» Тема урока: Одночлен. Стандартный вид одночлена Цель урока: познакомить обучающихся с понятием одночлен, стандартный вид одночлена, степень одночлена.Задачи: Повторим! Представить в виде степени с основанием аа) (а3) 4;б) а5 а 8 а 2;в) Найти значение выражения Каким числом (положительным или отрицательным) будет значение выражения? (-8)10; Прочитайте выражения6x2у; x3; mn7; ab; -8 ; х.ОПРЕДЕЛЕНИЕ: ? Вопрос--Как вы думаете является ли алгебраическое выражение одночленом Выберите одночлены Какие свойства умножения вы знаете? 2х2у∙9y2  и 8х∙9ху ОПРЕДЕЛЕНИЕ: одночлен называется одночленом стандартного вида, если имеет 1 числовой множитель, стоящий Алгоритм приведение одночлена к стандартному виду:Перемножить все числовые множители и поставить их Пример. Привести одночлен к стандартному виду:а) 3x2yz*(-2)xy2z5 == 3*(-2)x2xyy2zz5 = = Прочитайте те одночлены, которые записаны в стандартном виде. Назовите их коэффициенты. Степенью одночлена называется сумма показателей степеней всех переменных.Чтобы определить степень одночлена, нужно сложить показатели Назовите степень одночлена 1) 54авс5 Одночлены, у которых произведения переменных равны, хотя их порядок может отличаться, называются подобными Заполните таблицу Проверь! Выполните умножение: Решение упражнений № 156, 158. Подведение итоговЧто же такое одночлен?Одночлен, какого вида называют стандартным одночленом?Что называется степенью одночлена? Домашнее задание.Пункт 1.1 стр. 38, №155(1-4), №159(1-3)
Слайды презентации

Слайд 2 «Я слышу-я забываю, я вижу- я запоминаю, я

«Я слышу-я забываю, я вижу- я запоминаю, я делаю- я понимаю»

делаю- я понимаю»

(Китайская мудрость)
Девиз урока:
«Я слышу- я вижу- я делаю»

Слайд 3 Тема урока: Одночлен. Стандартный вид

Тема урока: Одночлен. Стандартный вид одночлена

одночлена

Слайд 4 Цель урока: познакомить обучающихся с понятием одночлен, стандартный

Цель урока: познакомить обучающихся с понятием одночлен, стандартный вид одночлена, степень

вид одночлена, степень одночлена.
Задачи: изучить и закрепить отличительные свойства

одночлена от алгебраических выражений;
Научить приводить одночлен к стандартному виду, определять степень одночлена;
Развивать умения сравнивать, выявлять закономерности, обобщать, продолжать развивать навыки выполнения действий со степенями;
Воспитывать активность, самостоятельность.

Слайд 5 Повторим!

Повторим!

Слайд 6 Представить в виде степени с

Представить в виде степени с основанием аа) (а3) 4;б) а5 а 8 а 2;в)

основанием а
а) (а3) 4;
б) а5 а 8 а 2;
в) а 4 : а2 а0;
г) а n а 3 : а2;
д) а6 а 13       а 

Слайд 7 Найти значение выражения

Найти значение выражения

Слайд 8 Каким числом (положительным или отрицательным) будет значение выражения?

Каким числом (положительным или отрицательным) будет значение выражения? (-8)10; (-5)27;

(-8)10; (-5)27;

75;
-28; -(-1)7 ; +(-32х2).

Слайд 9 Прочитайте выражения
6x2у; x3; mn7; ab;

Прочитайте выражения6x2у; x3; mn7; ab; -8 ; х.ОПРЕДЕЛЕНИЕ: Одночлен – это

-8 ; х.

ОПРЕДЕЛЕНИЕ: Одночлен – это произведение

чисел, переменных и степеней переменных, либо число, переменная, степень переменной.

Слайд 10 ? Вопрос
--Как вы думаете является ли
алгебраическое выражение

? Вопрос--Как вы думаете является ли алгебраическое выражение одночленом


одночленом или нет?

- является

Слайд 11 Выберите одночлены

Выберите одночлены

Слайд 12 Какие свойства умножения вы знаете?

Какие свойства умножения вы знаете? Переместительное :

Переместительное :

a∙b=b∙a

Сочетательное:
a∙(b∙c)=(a∙b)∙c

Слайд 13 2х2у∙9y2

2х2у∙9y2  и 8х∙9ху Воспользуемся переместительным и

 и 8х∙9ху

Воспользуемся переместительным

и сочетательным законами умножения.

2∙9∙х2 ∙у∙y2=18х2y3 и 8∙9∙х∙х∙у=72х2у

Слайд 14 ОПРЕДЕЛЕНИЕ: одночлен называется одночленом стандартного вида, если имеет

ОПРЕДЕЛЕНИЕ: одночлен называется одночленом стандартного вида, если имеет 1 числовой множитель,

1 числовой множитель, стоящий на первом месте (коэффициент), произведение

одинаковых переменных в нем записано в виде степени.
ОПРЕДЕЛЕНИЕ: числовой множитель одночлена, записанного в стандартном виде, называется коэффициентом одночлена.
Коэффициенты 1 и −1 обычно не записываются.
Например: 1ay2=ay2 ; -1x3=-x3

Слайд 15 Алгоритм приведение одночлена
к стандартному виду:

Перемножить все числовые

Алгоритм приведение одночлена к стандартному виду:Перемножить все числовые множители и поставить

множители и поставить их произведение на первое место;
Перемножить все

имеющиеся степени с одним буквенным основанием;
Перемножить все имеющиеся степени с другим буквенным основанием и т.д.


Слайд 16 Пример. Привести одночлен к стандартному виду:

а) 3x2yz*(-2)xy2z5

Пример. Привести одночлен к стандартному виду:а) 3x2yz*(-2)xy2z5 == 3*(-2)x2xyy2zz5 = =

=
= 3*(-2)x2xyy2zz5 =
= -6x3y3z6

b) -2ax2y3zn * 0,5ax5yz

=
=-2*0,5aax2x5y3yznz =
= - a2x7y4zn+1

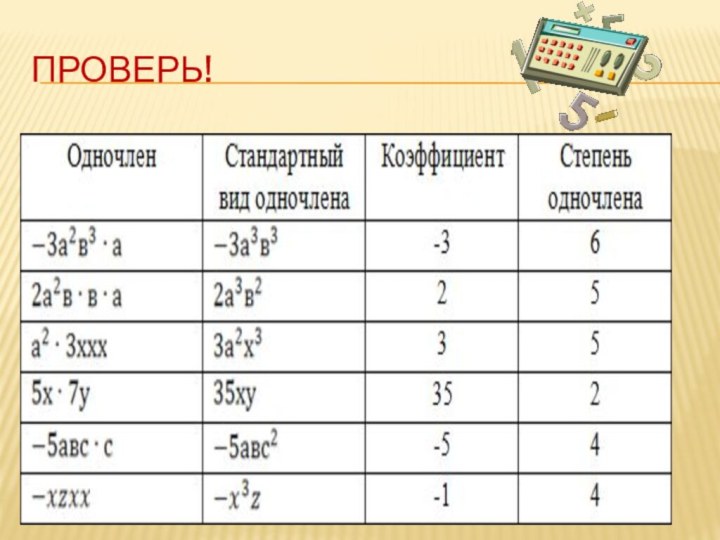
Слайд 17 Прочитайте те одночлены, которые записаны в стандартном виде.

Прочитайте те одночлены, которые записаны в стандартном виде. Назовите их коэффициенты.

Назовите их коэффициенты.

Слайд 18 Степенью одночлена называется сумма показателей степеней всех переменных.
Чтобы определить степень

Степенью одночлена называется сумма показателей степеней всех переменных.Чтобы определить степень одночлена, нужно сложить

одночлена, нужно сложить показатели степеней всех переменных (букв).
−12x4 y3 является

одночленом седьмой степени (4+3=7);
6a - одночлен первой степени (переменная a в первой степени);
7 - одночлен нулевой степени.

Слайд 19 Назовите степень одночлена

 1) 54авс5

Назовите степень одночлена 1) 54авс5 2)

2)

–6х5у3  3) 15 а2вс 4) 3х2в 5) –4 авс5

Слайд 20 Одночлены, у которых произведения переменных равны, хотя их

Одночлены, у которых произведения переменных равны, хотя их порядок может отличаться,

порядок может отличаться, называются подобными одночленами.
Подобными одночленами являются:
3х2 у и

-4х2у; 2вав и 5ав2; 6kx и хk; 5 и -3; х и ¾х.

Подобными одночленами
не являются:
  х2у и ху2

Слайд 21 Заполните таблицу

Заполните таблицу

Слайд 22 Проверь!

Проверь!

Слайд 23
Выполните умножение:



Выполните умножение:



Слайд 24 Решение упражнений № 156, 158.

Решение упражнений № 156, 158.

Слайд 25 Подведение итогов
Что же такое одночлен?

Одночлен, какого вида называют

Подведение итоговЧто же такое одночлен?Одночлен, какого вида называют стандартным одночленом?Что называется степенью одночлена?

стандартным одночленом?

Что называется степенью одночлена?

Слайд 26

Слайд 27 Домашнее задание.
Пункт 1.1 стр. 38, №155(1-4), №159(1-3)

Домашнее задание.Пункт 1.1 стр. 38, №155(1-4), №159(1-3)
  • Имя файла: prezentatsiya-po-algebre-na-temu-odnochlen-7-klass.pptx
  • Количество просмотров: 145
  • Количество скачиваний: 0
- Предыдущая ШАБЛОН ПРЕЗЕНТАЦИИ К УРОКАМ ОКРУЖАЮЩЕГО МИРА
Следующая - Презентация по английскому языку Step 2

Похожие презентации

Закрепление основных разделов из курса Алгебра и начала анализа. 10 – 11 класс Закрепление основных разделов из курса Алгебра и начала анализа. 10 – 11 класс 166
ПрезентацияОбласть определения тригонометрических функций(11 класс,профильное обучение) ПрезентацияОбласть определения тригонометрических функций(11 класс,профильное обучение) 157
Производная Производная 155
Решение квадратного уравнения Решение квадратного уравнения 154
Урок-презентация по теме Неравенство треугольникагеометрия 7 класс Урок-презентация по теме Неравенство треугольникагеометрия 7 класс 230
Бином Ньютона Бином Ньютона 154
Координаты для координатной плоскости Координаты для координатной плоскости 193
Презентация к внеклассному мероприятию Математические игры Юных энтузиастов по дисциплине Математика 10-11 класс Презентация к внеклассному мероприятию Математические игры Юных энтузиастов по дисциплине Математика 10-11 класс 160
Презентация по математике Повторение курса алгебры(9 класс) Презентация по математике Повторение курса алгебры(9 класс) 181
Применение производной к исследованию функции Применение производной к исследованию функции 126
Старинные задачи на дроби Старинные задачи на дроби 217
Методика обучения решению линейных неравенств с одной переменной Методика обучения решению линейных неравенств с одной переменной 145
Решение логических задач средствами алгебры логики Решение логических задач средствами алгебры логики 150
Графики функций y=ах2+n и y=а(х-m)2 Графики функций y=ах2+n и y=а(х-m)2 225
Размещение элементов Размещение элементов 194
Остовное дерево Остовное дерево 223
Анализ геометрических высказываний - 6 Анализ геометрических высказываний - 6 161
Өрнектерді түрлендіруде негізгі тригонометриялық тепе – теңдікті қолдану Өрнектерді түрлендіруде негізгі тригонометриялық тепе – теңдікті қолдану 216
Презентация по математике на тему ЕНТ Презентация по математике на тему ЕНТ 236
Интегралы 11 класс Интегралы 11 класс 201
Презентация по алгебре Логарифм и его свойства (10 класс) Презентация по алгебре Логарифм и его свойства (10 класс) 179
Тригонометрические неравенства Тригонометрические неравенства 145
Клуб супер математиков Клуб супер математиков 173
Презентация по алгебре и началам анализа на тему Периодичность функций y=sinx и y=cosx (10 класс) Презентация по алгебре и началам анализа на тему Периодичность функций y=sinx и y=cosx (10 класс) 180
Презентация по математике на тему Показательная функция (11 класс) Презентация по математике на тему Показательная функция (11 класс) 70
Презентация по алгебре на тему: Построение графика квадратичной функции (9 класс) Презентация по алгебре на тему: Построение графика квадратичной функции (9 класс) 148
Презентация к уроку математики в 10 классе по теме Логарифмическая функция, ее график и свойства Презентация к уроку математики в 10 классе по теме Логарифмическая функция, ее график и свойства 211
Презентация по решению задач по теории вероятностей Презентация по решению задач по теории вероятностей 164
Метод Гаусса и Крамера Метод Гаусса и Крамера 218
Презентация Интерактивный тренажер по теме Корень n-ой степени Презентация Интерактивный тренажер по теме Корень n-ой степени 166