Слайд 2
Начальные сведения
Понятие параметра. Контрольные значения параметра
Количество корней квадратного
и линейного уравнений с параметром
Знаки корней квадратного уравнения
с параметром.
Расположение корней квадратного трёхчлена на координатной прямой
Исследование квадратичной функции
Слайд 3
Приемы решения
Разбиение уравнения на два уравнения
Уединение параметра
Применение
монотонности функций при решении задач с параметрами
Применение метода областей
для решения задач с параметром
Применение чётности функций при решении задач с параметром
Применение инвариантности при решении заданий с параметром
Применение графических интерпретаций при решении заданий с параметром
Применение геометрических интерпретаций
Слайд 4
Уравнением ( неравенством ) с параметром называется
семейство уравнений ( неравенств ) одного вида, коэффициенты которых
вычисляются по одним и тем же формулам, зависящим от параметра ( параметров ).
Определение
Слайд 5
Под областью изменения параметра обычно подразумевают ( если
не сделано специальных оговорок ) множество всех действительных чисел.
Допустимыми значениями параметра a считаются все те значения a, при кото -рых выражения, входящие в уравнение ( неравенство ), имеют смысл.
Слайд 6
Определение
Решить уравнение
(с переменной х и
параметром а) - это значит решить семейство уравнений при
всех действительных значениях параметра.
Слайд 7
Определение
Контрольными значениями параметра
называются те
допустимые значения параметра, при которых или при переходе через
которые происходят качественные изменения уравнения
Слайд 8
Определение
Качественными изменениями уравнения являются изменения
способа поиска решения уравнения,
количества его корней
формул, по которым они вычисляются
Слайд 9
Контрольными значениями параметра линейного уравнения являются
те значения параметра, для которых коэффициент при х обращается
в нуль.
kx = b
Слайд 10
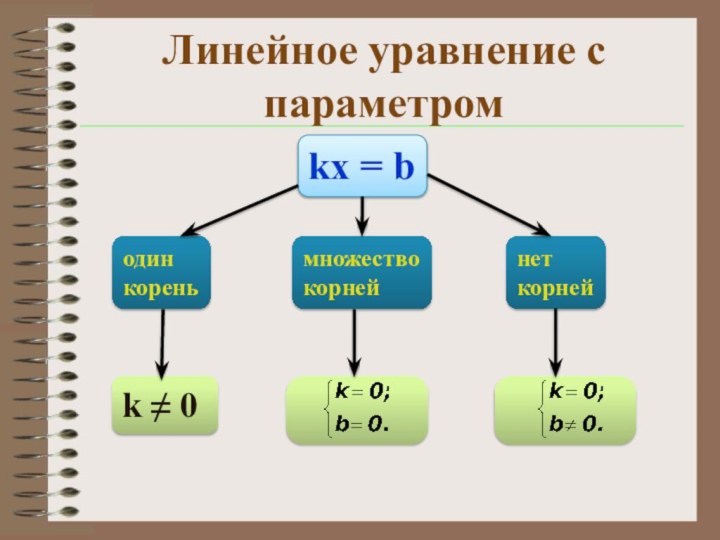
Линейное уравнение с параметром
kx = b
один
корень
множество
корней
нет
корней
k
≠ 0
Слайд 11
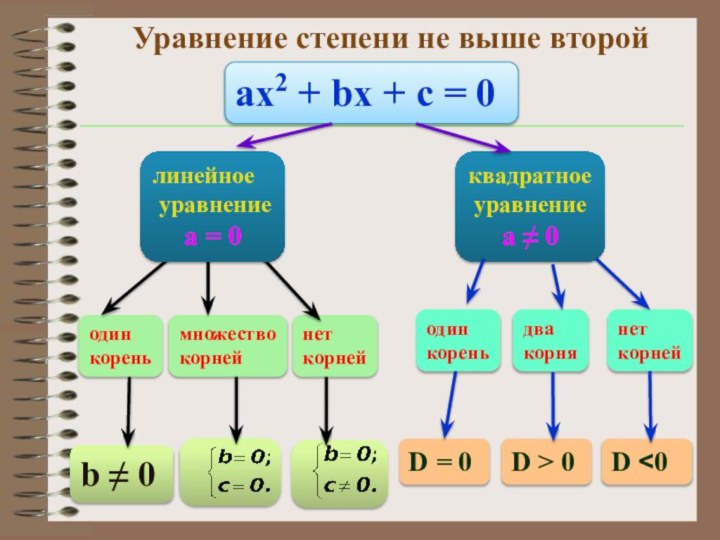
Уравнение степени не выше второй
ах2 + bx +
с = 0
один
корень
множество
корней
нет
корней
b ≠ 0
линейное
уравнение
а
= 0
квадратное
уравнение
а ≠ 0
один
корень
нет
корней
D = 0
D <0
два
корня
D > 0
Слайд 12
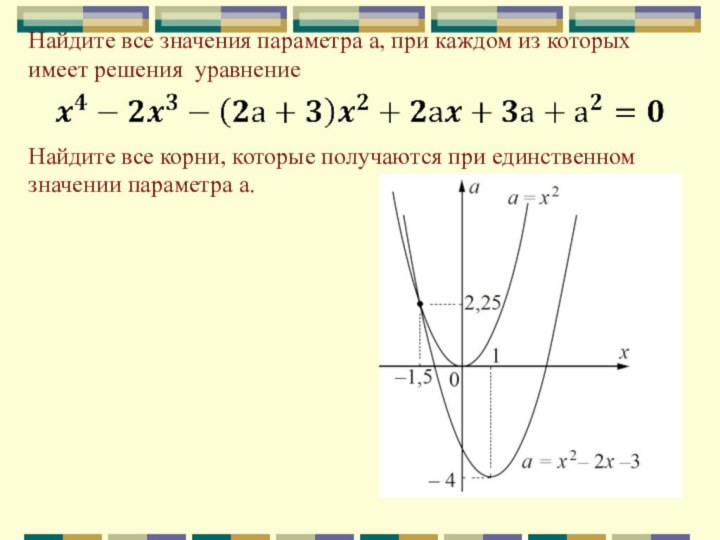
Найдите все значения параметра а, при каждом
из которых имеет решения уравнение
Найдите все корни, которые
получаются при единственном значении параметра а.
Задание №1
Слайд 13
Найдите все значения параметра а, при каждом из
которых имеет решения уравнение
Найдите все корни, которые получаются
при единственном значении параметра а.
Слайд 19
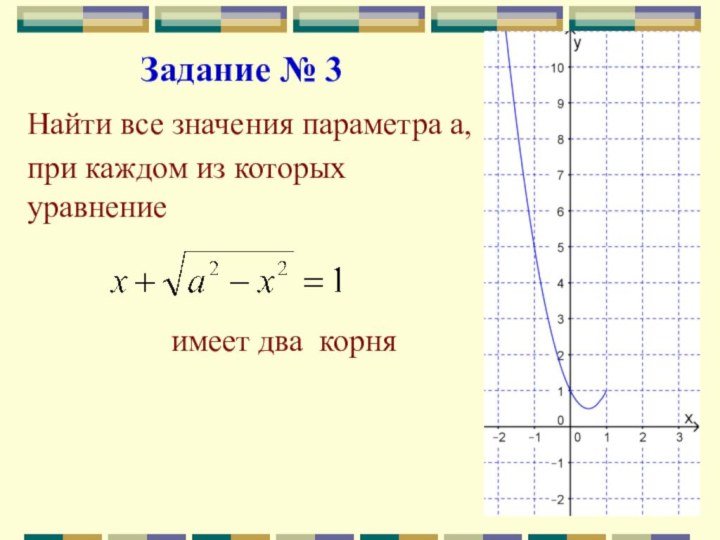
Найти все значения параметра a,
при каждом из которых
уравнение
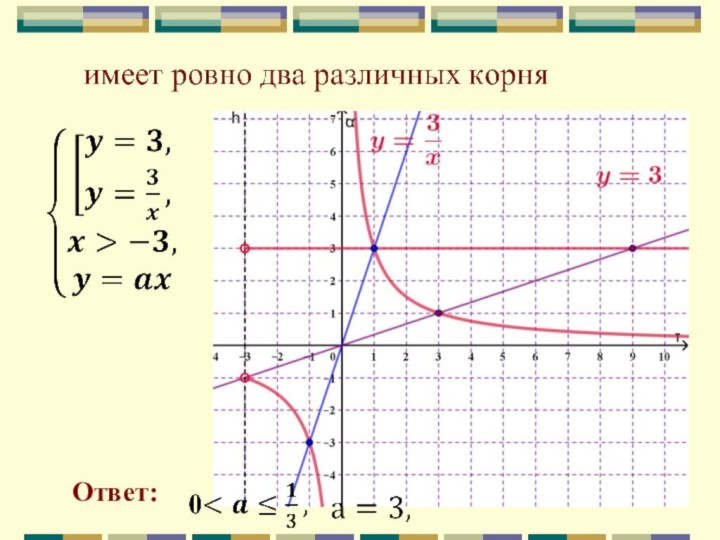
имеет два корня
Задание № 3
Слайд 20
Найти все значения параметра a,
при каждом из которых
уравнение
имеет два корня
Задание № 3
Слайд 21
Найдите все значения а при каждом из которых
уравнение
имеет хотя бы одно
решение
Задание № 4
Слайд 22
Применение монотонности функций
при решении заданий
с параметром
Слайд 23
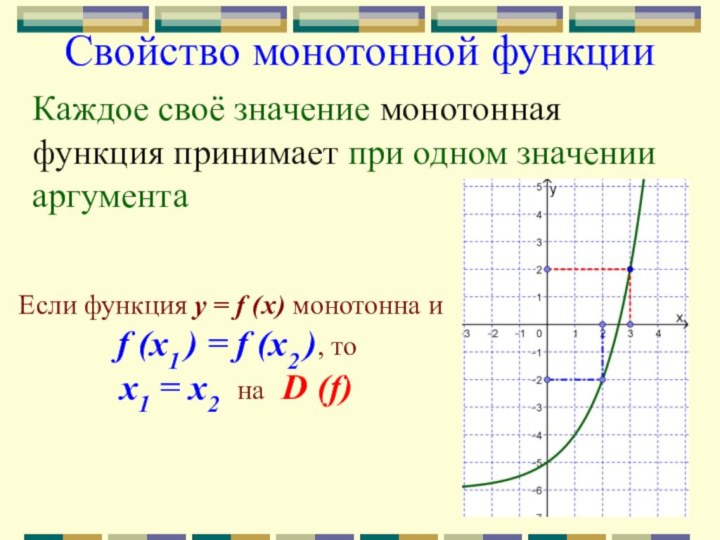
Свойство монотонной функции
Каждое своё значение монотонная функция принимает
при одном значении аргумента
Если функция у = f (x)
монотонна и
f (x1 ) = f (x2 ), то
x1 = x2 на D (f)
Слайд 24
Найдите все значения параметра а, при каждом из
которых уравнение
Имеет хотя бы одно решение.
Задание №
5
Если функция у = f (x) монотонна и
f (x1 ) = f (x2 ), то
x1 = x2 на D (f)
Слайд 26
Применение монотонности функций
Задание № 6
Слайд 27
Применение монотонности функций
Задание № 7
Слайд 28
Для каждого значения параметра a
найти корни уравнения
arcsin (ax2
– ax – 1) + arcsin x = 0
Задание
№ 8
Слайд 29
Применение замены переменных при решении заданий с
параметром
Слайд 30
Найти все значения параметра a при которых
уравнение
имеет корни
имеет два корня
один корень
Не имеет корней
Задание
№ 9
Слайд 31
Найти все значения параметра a при которых
уравнение
1) имеет корни; 2) имеет два корня; 3) один
корень; 4) не имеет корней
1. Есть корни
2. Два корня
3. Один корень
4. Нет корней
Слайд 32
1. Найти все значения параметра a при
которых уравнение
имеет корни
Задание № 10
Слайд 35
2. При каких значениях а уравнение
имеет два
корня?
Задание № 11
Слайд 38
Решение неравенств с двумя переменными (метод областей)
При решение
неравенств с двумя переменными
Представь неравенство в виде
f(x;y) 0
Построй график ограничивающей область линии (границу области f(x;y) = 0) пунктирной линией при строгом знаке, сплошной линией при нестрогом знаке неравенства.
Определи знак f(x;y) в каждой получившейся области, взяв точку с конкретными координатами из этой области и подставив их в выражение f(x;y) .
При наличии параметра возьми конкретное любое значение и определи знак f(x;y) в каждой получившейся области.
Заштрихуй области знака, заданного неравенством.
Слайд 39
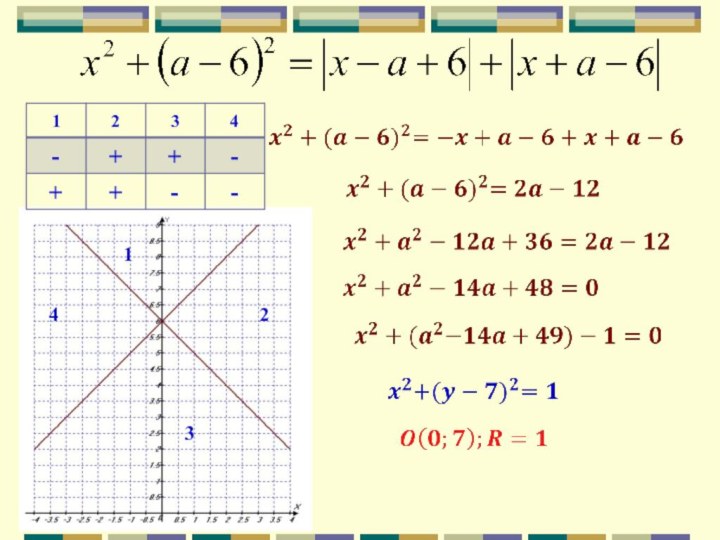
При наличии квадратов переменных в уравнении линии
Если нет
чётко выраженного известного вида уравнения, раскройте скобки, перегруппируйте слагаемые
по переменным х и у.
Если есть первая степень и квадрат одной и той же переменной, выделите квадрат двучлена.
Если между квадратами (квадратами двучленов) переменных х и у стоит «плюс» , попробуйте сведи к уравнению окружности
(х – х0)2 + (у – у0)2 = R2
Если между квадратами (квадратами двучленов) переменных х и у стоит «минус» , попробуйте разложить на множители, используя разность квадратов, свести уравнение к произведению равному нулю.
Слайд 40
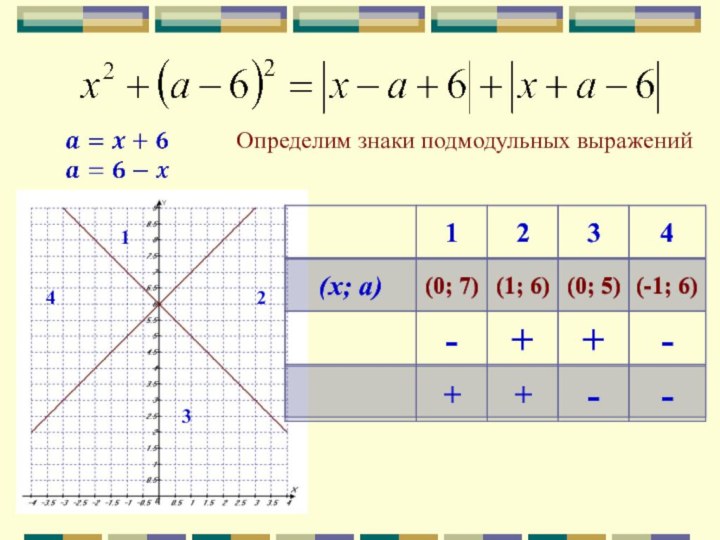
Найдите все значения а при каждом из которых
уравнение
имеет единственное решение
Задание №
12
Слайд 41
1
2
3
4
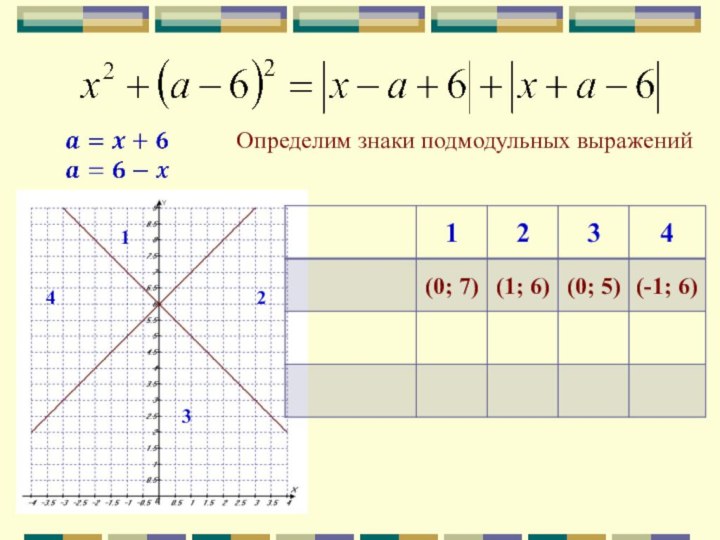
Определим знаки подмодульных выражений
Слайд 42
1
2
3
4
Определим знаки подмодульных выражений
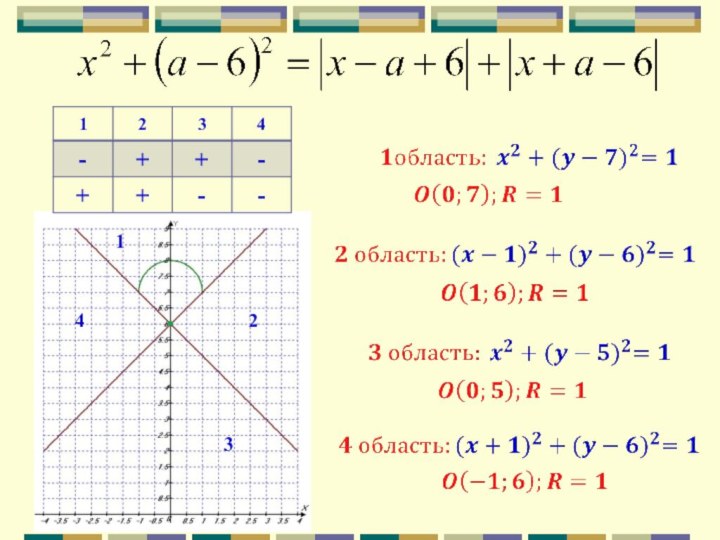
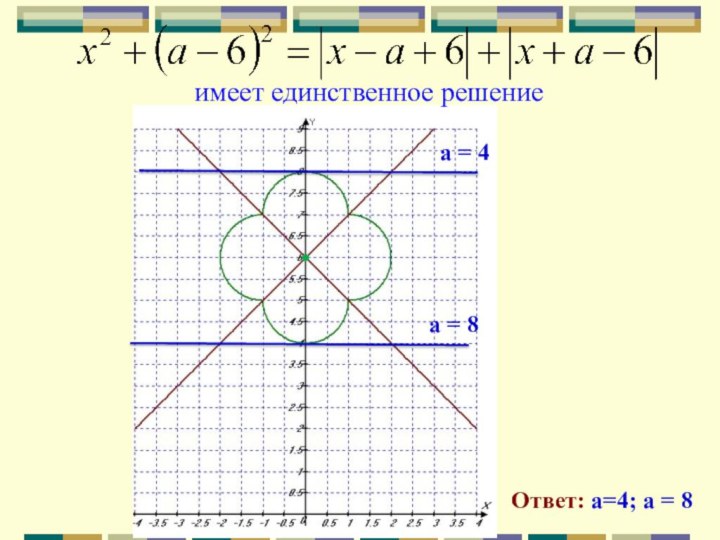
Слайд 45
имеет единственное решение
Ответ: а=4; а = 8
а
= 4
а = 8
Слайд 46
Найти все значения параметра а при
каждом из которых на интервале (1; 2) существует хотя
бы одно число х,
не удовлетворяющее неравенству
Задание № 13
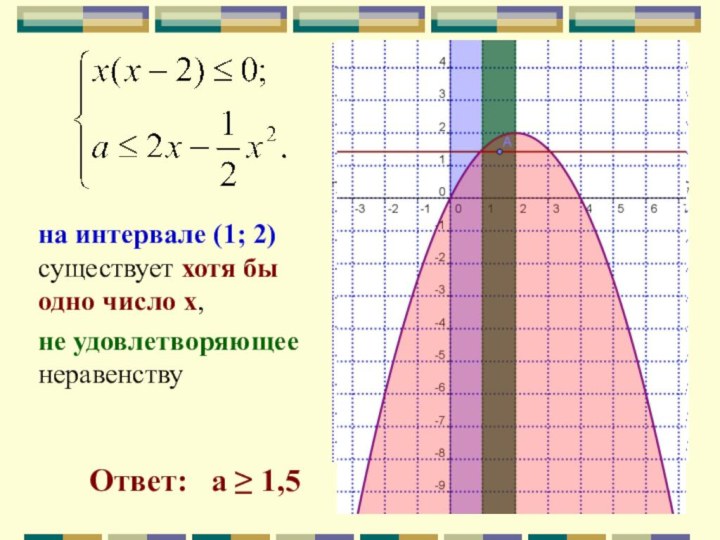
Слайд 49
Ответ: а ≥ 1,5
на интервале (1; 2)
существует хотя бы одно число х,
не удовлетворяющее неравенству
Слайд 52
Применение четности (нечетности) функций
при решении
заданий с параметром
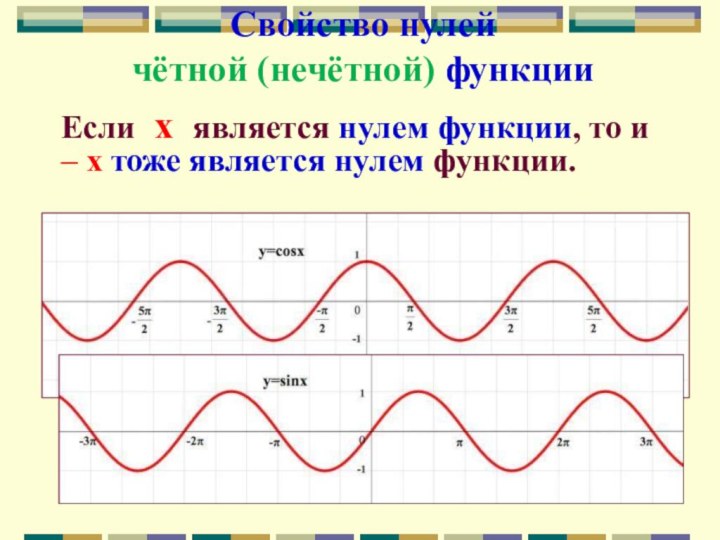
Слайд 53
Если х является нулем функции, то и
– х тоже является нулем
функции.
Свойство нулей
чётной (нечётной) функции
Слайд 54
Если х = о является нулем четной (нечётной)
функции, то функция имеет нечётное количество нулей.
Если х =
о не является нулем четной (нечётной) функции, то функция имеет чётное количество нулей.
Свойство нулей
чётной (нечётной) функции
Слайд 55
Достаточное условие
наличия
у уравнения нечётного количества корней
( необходимое для единственного корня )
Если функция у =f(x) – чётная (нечётная), то уравнение f(x) = 0 имеет нечетное количество корней (единственный корень), если х = 0 является корнем уравнения.
Это условие необходимое для наличия единственного корня, но не достаточное! Требуется всегда проверка, сколько корней имеет уравнение при найденных значениях параметра
Слайд 56
Функция y= f(x) чётной
f(-x) = f(x)
Т.е функция
инвариантна (неизменна)
при подстановке –x вместо х
Поэтому единственный корень
(нечётное
количество корней) уравнение имеет, если
–x = х, т.е х = 0 – корень уравнения
Слайд 57
Найдите все значения а при каждом из которых
уравнение
имеет единственное решение
Задание №
15
Слайд 58
Задание № 15
Если х0 является корнем исходного
уравнения, то и -х0 является его корнем. Значит, исходное уравнение
имеет нечётное число корней, только если х = 0 является корнем уравнения
Слайд 59
Задание 15
Подставим х = 0 в уравнение
Слайд 60
При а =6
х = 0; х = 2;
х = -2 – три корня (не единственный)
При а
= 4 и а = 8
Слайд 61
При а = 4 и а = 8
уравнение
имеет единственный корень
х = 0
Ответ: При а = 4;
а = 8 уравнение имеет единственный корень
Решим графически
Слайд 62
Найдите все значения параметра, при каждом из которых
уравнение
имеет единственное решение.
Задание 16
Использование чётности (симметричности) функций
Слайд 63
Пусть t = x – 1, тогда
уравнение примет вид
Функция четная
Если х0 является корнем исходного уравнения, то
и -х0 является его корнем. Значит, исходное уравнение имеет нечётное число корней, только если х = 0 является корнем уравнения
Слайд 64
Подставим t = 0 в уравнение
Пусть
t = , тогда уравнение примет вид
Слайд 66
при t R
При а = -1 уравнение
имеет единственный корень
Ответ: а = -1
Слайд 67
При поиске параметра при котором уравнение имеет единственный
корень:
если функция у =f(x) – чётная (нечётная), то уравнение
f(x) = 0 имеет единственный корень, если х = 0 является корнем уравнения.
Поэтому надо подставить х = 0 в уравнение и найти соответствующие значения параметра а.
Но надо помнить, что это условие необходимое, но не достаточное! Оно гарантирует нечетное количество корней, но не обязательно единственный корень.
Требуется всегда проверка, сколько корней имеет уравнение при найденных значениях параметра. Удобно во многих случаях делать проверку графически.
Часто требуется сделать некоторую замену, чтобы получить четную функцию.
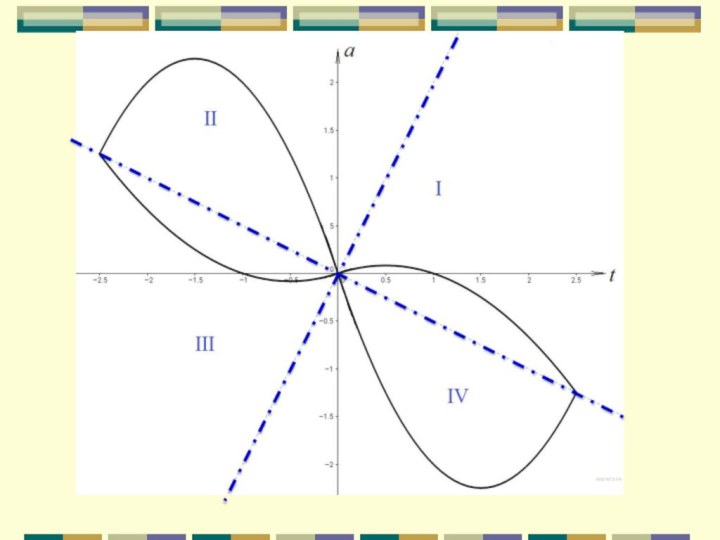
Слайд 68
Применение геометрической информации
Слайд 71
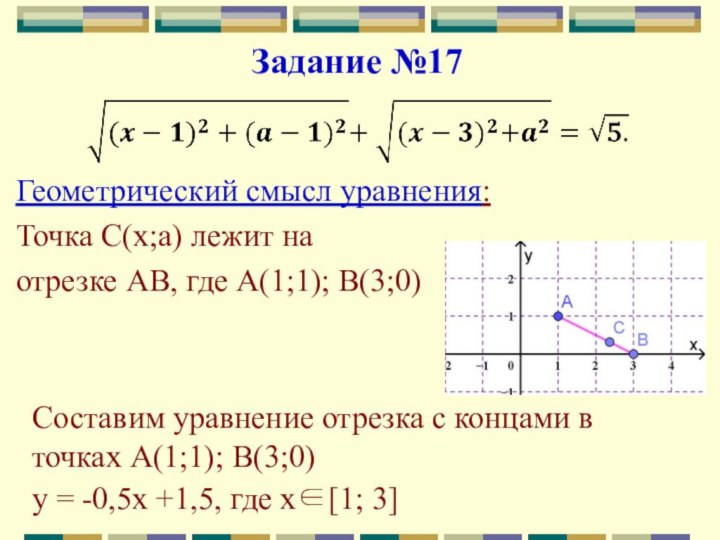
Задание №17
Геометрический смысл уравнения:
Точка С(х;a) лежит на
отрезке
АВ, где А(1;1); В(3;0)
Составим уравнение отрезка с концами в
точках А(1;1); В(3;0)
у = -0,5х +1,5, где х[1; 3]
Слайд 72
Задание №17
Точка С(х;a) лежит на отрезке АВ,
у =
-0,5х +1,5, где х[1; 3]
a = -0,5х
+1,5, где х[1; 3]
Слайд 73
Задание №17
a = -0,5х +1,5, где х[1; 3]
Подставим значение а в уравнение
Слайд 74
Применение графических иллюстраций
при решении заданий
с параметром
Слайд 81
Применение монотонности функций
Слайд 82
Применение монотонности функций



















![Приемы решения задач с параметром Задание № 5Ответ: а[-4; 2]](/img/tmb/6/580480/f4e9e9039c996aec78e3c029fa2916fe-720x.jpg)

















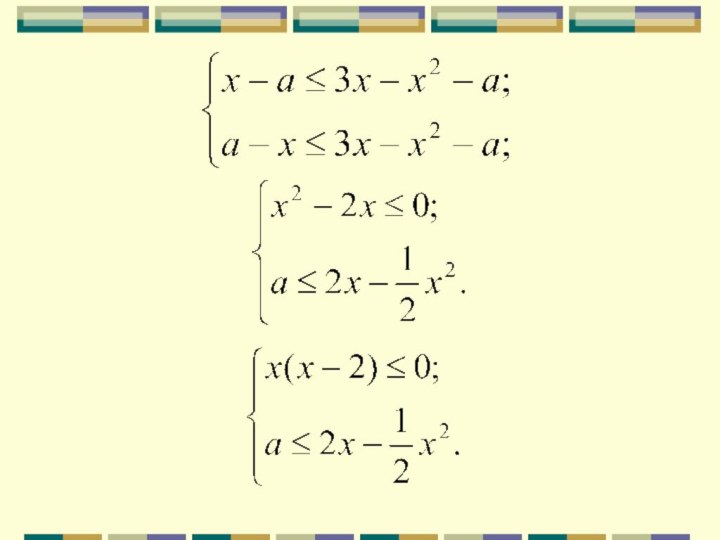




















![Приемы решения задач с параметром Задание №17a = -0,5х +1,5, где х[1; 3] Подставим значение а в уравнение](/img/tmb/6/580480/af28286fa0ee6245fb23232e7a2366ac-720x.jpg)