- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике Метод вспомогательной окружности
Содержание
- 2. Суть метода заключается в том, что при
- 3. Анализ решения достаточно большого круга задач показывает,
- 4. Целесообразность применения метода зависит от этих
- 5. В процессе изучения метода вспомогательной окружности
- 6. Вот эти признаки. 1) Если дан
- 7. Четыре различные точки A, B, C,
- 8. 4) диагонали четырехугольника ABCD пересекаются в
- 9. Опорные задачи на метод вспомогательной окружностиЗадача
- 10. Задача 2. В остроугольном треугольнике АВС
- 11. Задача 2. В остроугольном треугольнике АВС
- 12. Задача 3. Через некоторую точку плоскости проведены
- 13. Задача 3. Через некоторую точку плоскости проведены
- 14. Задача 4. Медиана и высота треугольника, проведенные
- 15. Задача 4. Медиана и высота треугольника, проведенные
- 16. Задача 5№16 ЕГЭ. Точки D и Е
- 17. Пусть теперь треугольник ABC тупоугольный и, например,
- 18. Пусть теперь а > 90° (рис. 3).
- 19. ЕГЭ.№16Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне
- 20. Решение.а) По теореме о внешнем угле треугольника
- 21. ЕГЭ №16(2015г)В остроугольном треугольнике ABC проведены высоты AP и CQ.а) Докажите, что
- 22. В остроугольном треугольнике ABC проведены высоты AP и CQ.а) Докажите, что угол PAC равен
- 23. Егэ 2016 г
- 25. Задачи .1.Дана трапеция АВСD,диагонали АС И ВD
- 26. Скачать презентацию
- 27. Похожие презентации
Суть метода заключается в том, что при решении планиметрических задач, когда требуется установить связь между данными и искомыми величинами, нередко полезно около треугольника или четырехугольника описать окружность, после чего эти связи становятся более ощутимыми или даже






















Слайд 3 Анализ решения достаточно большого круга задач показывает, что
использование вспомогательной окружности связано с характерными признаками фигуры, рассматриваемой
в задаче.Слайд 4 Целесообразность применения метода зависит от этих признаков.
А они основаны на теоремах и их следствиях, изучаемых
в курсе геометрии 8, 9 классов.Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность, прямой.
Угол, с вершиной внутри круга, измеряется полусуммой двух дуг, одна из которых расположена внутри этого угла, а другая – внутри угла, вертикального к данному.
Угол, вершина которого расположена вне круга, а каждая из сторон пересекает окружность в двух точках, измеряется полуразностью дуг, заключенного внутри угла.
Угол между касательной к окружности и хордой, проведенной через точку касания, измеряется половиной дуги, заключенной внутри этого угла.
В любой треугольник можно вписать окружность и притом единственную.
Около любого треугольника можно описать единственную окружность.
Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность, центр которой – точка пересечения диагоналей.
Около трапеции можно описать окружность только тогда, когда она равнобочная.
Слайд 5 В процессе изучения метода вспомогательной окружности необходимо
научиться выделять и использовать те признаки, наличие которых в
задаче приводит к построению вспомогательной окружности и с ее помощью устанавливать связи между необходимыми объектами и величинами, определенными условием задачи.
Слайд 6
Вот эти признаки.
1) Если дан правильный
треугольник, то можно провести окружность с центром в любой
из его вершин и радиусом, равным длине его стороны, либо описать около него окружность, которая разобьется вершинами треугольника на равные дуги по 1200 каждая.2) Если дан прямоугольный треугольник, то вокруг него описывается окружность, центром которой является середина гипотенузы, а радиус равен медиане, проведенной к гипотенузе этого треугольника.
3) Если удается установить, что суммы противоположных углов выпуклого четырехугольника равны, то вокруг него описывается окружность.
4) Если дан квадрат, прямоугольник или равнобедренная трапеция, то вокруг них описывается окружность.
Слайд 7 Четыре различные точки A, B, C, D
принадлежат одной окружности, если: 1) точки А и D расположены
в одной полуплоскости относительно прямой ВС и вы- полняется равенство ∠BDC = ∠BAC; 2) точки А и D расположены в разных полуплоскостях относительно прямой ВС и выполняется равенство ∠BDC + ∠BAC = 180° (иначе говоря, сумма двух противопо- ложных углов четырехугольника ABCD равна 180°); 3) точки А и D являются вершинами двух прямоугольных треугольников с общей гипотенузой ВС (и центр их общей описанной окружности О есть середина гипотенузы) — хотя это утверждение, по существу, и является простым следствием двух предыдущих, выделим его отдельным пунктом, поскольку им приходится пользоваться весьма часто;Слайд 8 4) диагонали четырехугольника ABCD пересекаются в точке Е
и при этом треугольники ABЕ и DСЕ подобны; 5) две
различные прямые АС и BD пересекаются в точке Е, причем выполняется соотношение: AE ⋅ EC = BE ⋅ ED; 6) произведение диагоналей четырехугольника ABCD равно сумме произведений противолежащих сторон: AВ ⋅ CD + BC ⋅ AD = AC ⋅ BD; 7) основания перпендикуляров, опущенных из точки D на прямые, содержащие стороны треугольника ABC, лежат на одной прямой.
Слайд 9
Опорные задачи на метод вспомогательной окружности
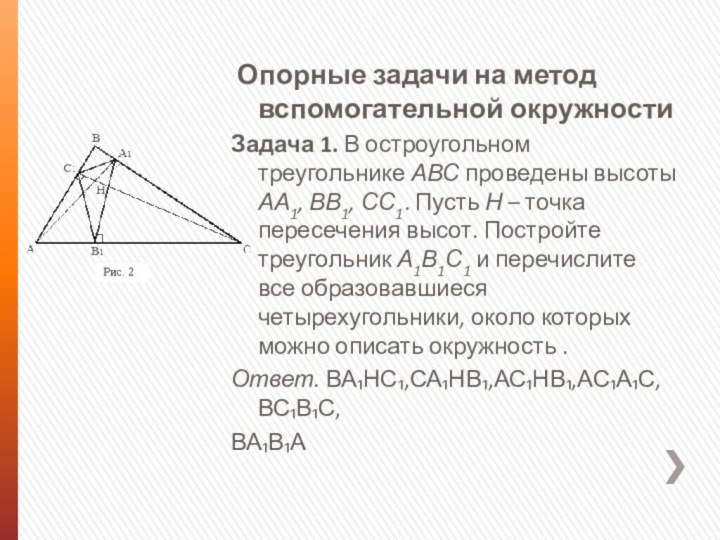
Задача 1.
В остроугольном треугольнике АВС проведены высоты АА1, ВВ1, СС1.
Пусть Н – точка пересечения высот. Постройте треугольник А1В1С1 и перечислите все образовавшиеся четырехугольники, около которых можно описать окружность .Ответ. ВА₁НС₁,СА₁НВ₁,АС₁НВ₁,АС₁А₁С,ВС₁В₁С,
ВА₁В₁А
Слайд 10
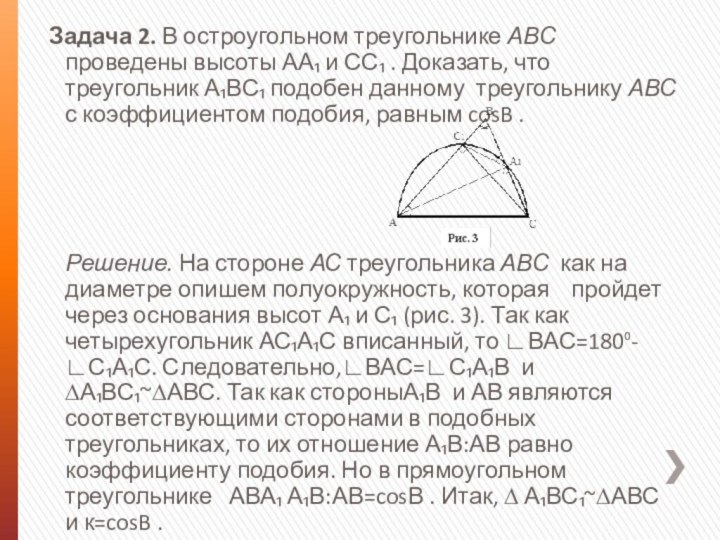
Задача 2. В остроугольном треугольнике АВС
проведены высоты АА₁ и СС₁ . Доказать, что треугольник
А₁ВС₁ подобен данному треугольнику АВС с коэффициентом подобия, равным cosB .Слайд 11 Задача 2. В остроугольном треугольнике АВС проведены
высоты АА₁ и СС₁ . Доказать, что треугольник А₁ВС₁
подобен данному треугольнику АВС с коэффициентом подобия, равным cosB .Решение. На стороне АС треугольника АВС как на диаметре опишем полуокружность, которая пройдет через основания высот А₁ и С₁ (рис. 3). Так как четырехугольник АС₁А₁С вписанный, то ∟ВАС=180⁰-∟С₁А₁С. Следовательно,∟ВАС=∟С₁А₁В и ∆А₁ВС₁~∆АВС. Так как стороныА₁В и АВ являются соответствующими сторонами в подобных треугольниках, то их отношение А₁В:АВ равно коэффициенту подобия. Но в прямоугольном треугольнике АВА₁ А₁В:АВ=cosВ . Итак, ∆ А₁ВС₁~∆АВС и к=cosB .
Слайд 12
Задача 3. Через некоторую точку плоскости проведены три
прямые так, что угол между любыми двумя из них
равен 600.Докажите, что основания перпендикуляров, опущенных из любой точки плоскости на эти прямые, служат вершинами равностороннего треугольника.Слайд 13 Задача 3. Через некоторую точку плоскости проведены три
прямые так, что угол между любыми двумя из них
равен 600.Докажите, что основания перпендикуляров, опущенных из любой точки плоскости на эти прямые, служат вершинами равностороннего треугольника.Решение. Пусть три данные прямые пересекаются в точке О; М – произвольная точка плоскости; А, В, и С основания перпендикуляров, опущенных из точки М на данные прямые (рис. 4). Точки О, М, А, В и С лежат на одной окружности с диаметром ОМ (обоснуйте это). Теперь видно, что , ∟АВС=∟АОС поскольку оба они опираются на одну и туже дугу АС. Значит,∟АВС=60⁰ . Точно так же ,∟АСВ=∟АОВ=60⁰, то есть треугольник АВС равносторонний
Слайд 14 Задача 4. Медиана и высота треугольника, проведенные из
одной вершины внутри него, различны и образуют равные углы
со сторонами, выходящими из той же вершины. Доказать, что треугольник прямоугольный.Слайд 15 Задача 4. Медиана и высота треугольника, проведенные из
одной вершины внутри него, различны и образуют равные углы
со сторонами, выходящими из той же вершины. Доказать, что треугольник прямоугольный.Решение. Пусть высота СН и медиана СМ
треугольника АВС образует со сторонами
АС и ВС равные углы (рис. 5).
Опишем около треугольника АВС окружность.
Достаточно доказать, что АВ – ее диаметр.
Продолжим медиану СМ до
пересечения с окружностью в точке D и рассмотрим
треугольники АСН и DCB. Так как
∟АСН=∟DCB по условию и ∟А=∟D как вписанные углы, опирающиеся на одну и ту же дугу, то ∟AHC=∟DBС=90⁰. Следовательно, CD диаметр окружности. Центр окружности лежит на диаметре CD и на серединном перпендикуляре m к стороне АВ. Так как по условию CD не является высотой, то прямые m и CD имеют только одну общую точку М, которая является центром описанной окружности. Следовательно, АВ – диаметр окружности и ∟ACB=90⁰.
Слайд 16
Задача 5
№16 ЕГЭ. Точки D и Е —
основания высот непрямоугольного треугольника ABC, проведенных из вершин А
и С соответственно.Известно, что DE/AC = k, ВС = а и АВ = b. Найдите сторону АС.
Решение.
Из точек D и Е сторона АС видна под прямым углом,
значит, эти точки лежат на окружности с диаметром АС.
Обозначим угол АВС = a.
Если треугольник АВС остроугольный (рис. 1), то
основания высот AD и СЕ лежат на сторонах
треугольника. Тогда четырехугольник AEDC —
вписанный, поэтому ∟BDE = 180° - ∟CDE = ∟САЕ= ∟CAB.
Треугольники EDB и CAB подобны (по двум углам) с
коэффициентомDE:АС=ВЕ:ВС= cosa, т.е. cosa = k. Тогда по теореме косинусов
АС2 = ВА2 + ВС2 - 2ВА • ВС cos а = b2 + а2 - 2аbк.
Слайд 17
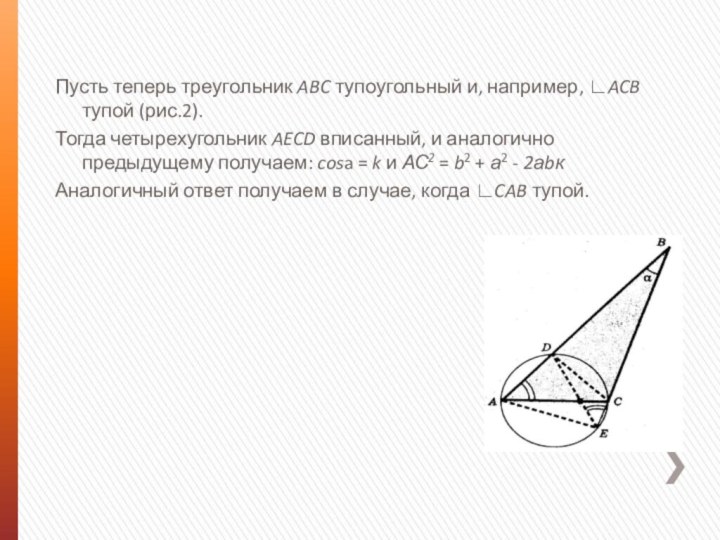
Пусть теперь треугольник ABC тупоугольный и, например, ∟ACB
тупой (рис.2).
Тогда четырехугольник AECD вписанный, и аналогично предыдущему получаем:
cosa = k и АС2 = b2 + а2 - 2аbкАналогичный ответ получаем в случае, когда ∟CAB тупой.
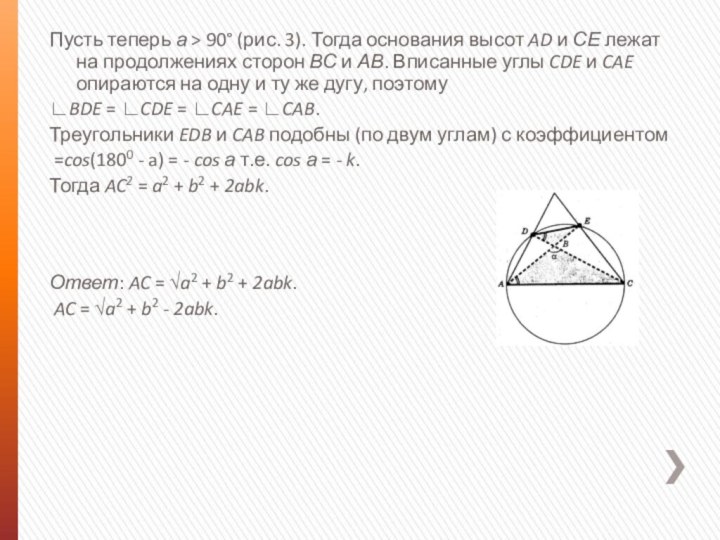
Слайд 18 Пусть теперь а > 90° (рис. 3). Тогда
основания высот AD и СЕ лежат на продолжениях сторон
ВС и АВ. Вписанные углы CDE и CAE опираются на одну и ту же дугу, поэтому∟BDE = ∟CDE = ∟CAE = ∟CAB.
Треугольники EDB и CAB подобны (по двум углам) с коэффициентом
=cos(1800 - a) = - cos а т.е. cos а = - k.
Тогда AC2 = a2 + b2 + 2abk.
Ответ: AC = √a2 + b2 + 2abk.
AC = √a2 + b2 - 2abk.
Слайд 19
ЕГЭ.№16
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника,
причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника
в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
Слайд 20
Решение.а) По теореме о внешнем угле
треугольника ∠BOC = ∠BAO + ∠АBO = 2 · 30° = 60°.
Поэтому
∟ВОС+∟ВЕС=60⁰+120⁰=180⁰
Значит, точки B, E, C, O лежат на одной окружности.
Вписанные
в эту окружность углы CBE и COE опираютсяна одну и ту же дугу, следовательно, ∠CBE = ∠COE.
б) По теореме косинусов ВС²=ВЕ²+СЕ²-2ВЕ·СЕ·соs120⁰,ВС=56
Вписанные углы BEO и CEO опираются на равные хорды BO и CO, значит, EO — биссектриса угла BEC. Пусть M — точка её пересечения со стороной BC. По формуле для биссектрисы треугольника получаем:
ЕМ=(2ВЕ·СЕ·cos(∟ВЕС/2))/(ВЕ+СЕ)=15
По свойству биссектрисы треугольника СМ/ВМ=СЕ/ВЕ=24/40=3/5, значит,
СМ=3/8·ВС=21,ВМ=35
По теореме о произведении пересекающихся хорд EM · MO = BM · CM, откуда находим, что МО=(ВМ·СМ)/ЕМ=49
Треугольники COM и AOK равны по стороне и двум прилежащим к ней
углам, поэтому OK = OM. Следовательно, EK = EM + 2OM = 15 + 98 = 113.
Ответ: 113.
Слайд 21
ЕГЭ №16(2015г)
В остроугольном треугольнике ABC проведены высоты AP и CQ.
а) Докажите, что угол PAC равен
углу PQC.
б) Найдите радиус окружности, описанной около треугольника ABC, если известно,
что PQ = 8 и ∠ABC = 60°
Слайд 22
В остроугольном треугольнике ABC проведены высоты
AP и CQ.
а) Докажите, что угол PAC равен углу PQC.
б)
Найдите радиус окружности, описанной около
треугольника ABC, если известно, что PQ = 8
и ∠ABC = 60°Решение.а) Углы APC и AQC — прямые, значит, точки A, Q, P и C лежат на одной окружности с диаметром AC, и, следовательно, равны и вписанные углы PAC и PQC этой окружности, опирающиеся на дугу PC, что и требовалось доказать.
б) Прямоугольные треугольники ABP и CBQ имеют общий угол ABC, следовательно, они подобны, откуда BQ/BP=BC/BA или BQ/BC=BP/BA , но тогда и треугольники BAC и BPQ также подобны, причем коэффициент подобия равен BQ/BP=BC/BA =cosB ,откуда АС=PQ/cosB=8/cos60⁰=16 Тогда радиус R окружности, описанной около треугольника ABC равен R=AC/sin60⁰=16/√3
Ответ: 16/√3
Слайд 25
Задачи .
1.Дана трапеция АВСD,диагонали АС И ВD которой
пересекаются под прямым углом, а продолжения боковых сторон АВ
и DС пересекаются в точке К под углом 30⁰.Известно что ∟ВАС=∟СDВ,а площадь трапеции S.Найдите площадь треугольника АКD. (1,5S или 0.5S)2.В треугольнике АВС проведены медиана ВМ и высота ВН ( А-Н-С),угол АВН равен углу СВМ,АВ=9,ВС=12
а)докажите, что АМ=ВМ
б) найдите длину НМ. (2,1)
3.Сторона треугольника √2,углы,прилежащие к ней,равны 75⁰ и 60⁰.Найдите отрезок,соединяющий основания высот,проведенных из вершин этих углов. (1)





























