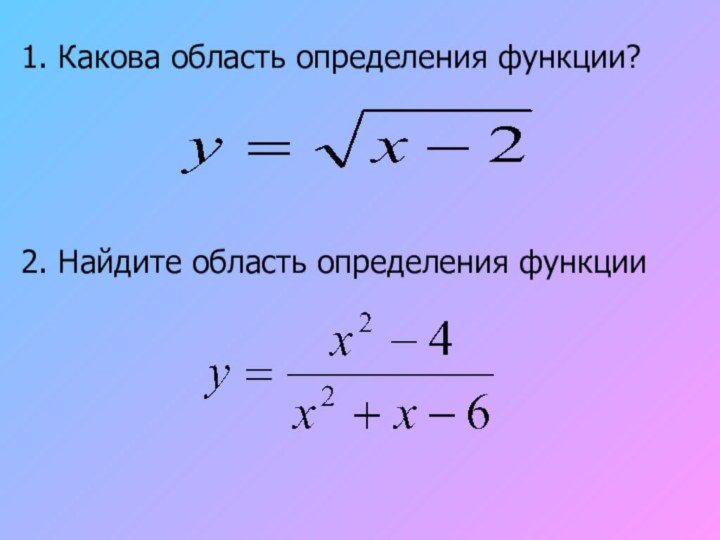Презентация на тему по алгебре Исследование функции с помощью производнолй

точки области определения функции являются критическими точками.
Необходимое условие экстремума

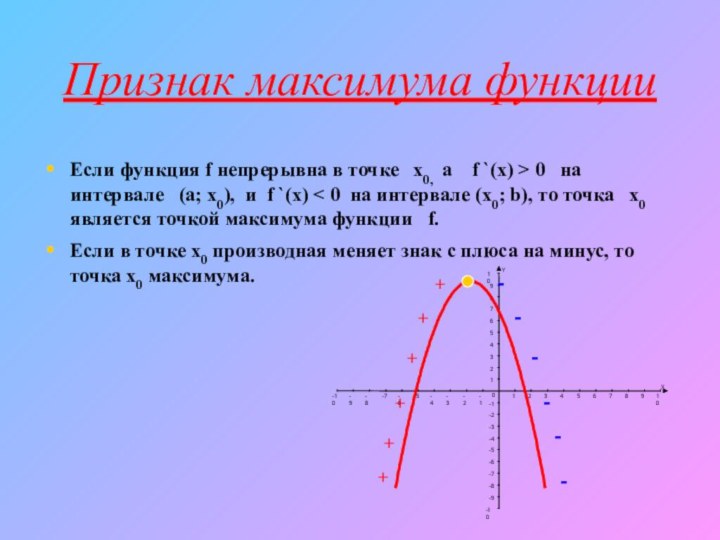
(или теорема французского математика – теорема Ферма)
Какая точка называется точкой максимума? (упрощенная формулировка этого признака).
Какая точка называется точкой минимума? (упрощенная формулировка этого признака)

имеет неотрицательную производную в каждой точке интервала (а;b),
то

функция f возрастает
на интервале (а;b).

неположительную производную в каждой точке интервала (а;b),
то функция

f убывает на интервале (а;b).

х0 является точкой экстремума функции f и в этой

точке существует производная f `(x), то она равна нулю: f `(x) = 0.

х0, а f `(x) > 0

на интервале (а; х0), и f `(x) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f.
Если в точке х0 производная меняет знак с плюса на минус, то точка х0 максимума.

х0, f `(x) < 0 на интервале (а; х0)

и f `(x) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f.
Если в точке х0 производная меняет знак с минуса на плюс, то х0 есть точка минимума.

экстремума

определения функции

на которых функция монотонно возрастает, убывает, имеет максимум, имеет

минимум.

точек максимума имеет эта функция? Назовите их.

По происхождению швейцарец. В 1726 был приглашен в Петербургскую

академию наук и переехал в 1727
в Россию.

множество значений переменной х, при которых данная функция определена).
Исследовать функцию

на четность. (Выяснить, симметрична ли область определения функции относительно начала координат и найти y = f(-x). Если f(-x) = f(x), то функция четная, если y f(-x) = -f(x), то функция нечетная).
Найти нули функции. (Точки пересечения с осями координат).
Исследовать функцию на монотонность. (Если f ’(x) > 0, то функция возрастает, если f ’(x) < 0, то функция убывает).
Записать точки экстремума и экстремумы функции. (Найти значение функции в точках экстремума).
Дополнительные точки.
Построение графика.

f ``(x) < 0
График вогнутый
f `(x) –

возрастает
f ``(x) > 0

α1

α2

A1

A2

A1

A2

если вам интересно,
Что точку разрыва и корень имею,
И есть

интервал, где расти не посмею.
Во всём остальном положительна, право,
И это, конечно, не ради забавы.
Для чисел больших я стремлюсь к единице.
Найдите меня среди прочих в таблице.

задание: найдите функции, описывающие реальные физические процессы, которые вы

изучали на уроках физики и исследуйте их.

Как влияет знак второй производной на выпуклость функции.

Выставление

оценок за фронтальный опрос, за блиц-опрос и за практическую работу у доски.

Будьте добры, покажите, пожалуйста, ваше настроение в конце нашего урока.