Слайд 2
Цель урока:
Образовательные:
систематизировать и обобщить знания по пройденной теме,
проверить уровень усвоения учащимися соответствующих формул и правил.
Развивающие:
углубить
знание учащихся, развить умение применять приемы сокращенного умножения при решении уравнений, при обнаружении и исправлении ошибок, объяснении своих действий, развитие творческой деятельности учащихся.
Воспитательные:
создание условий для включения каждого ученика в активную учебно-познавательную деятельность, где каждый может проявить себя, воспитание интереса к математике, расширение кругозора, включение в урок исторического материала.
Слайд 3
“
Предмет математики настолько серьезен, что полезно не упускать
случая сделать его занимательным.
Блез Паскаль.
Слайд 4
Устный счет
1.Представьте в виде квадрата положительного числа:
а) 81 ;
б) 0,04; в) 36 ;
49
3. Замените степень выражения одночленом стандартного вида:
а) (2x)²; б) (4m²)²; в) (- 6x³y)²;
г) (0,1mn³)².
Слайд 5
Какие формулы сокращенного умножения Вы знаете?
Слайд 6
Формулы сокращённого умножения
1) Квадрат суммы двух выражений
2) Квадрат
разности двух выражений
3) Разность квадратов двух выражений
Сумма кубов
двух выражений
Разность кубов двух выражений
Слайд 7
Установите соответствия между выражениями левого и
правого столбцов. Какое выражение осталось без пары? Почему?
I.Теоретический материал.
Слайд 9
Квадрат суммы двух выражений равен…
…квадрату первого выражения, плюс
удвоенное произведение первого и второго выражений, плюс квадрат второго
выражения.
Закончите формулировку
Слайд 10
Квадрат разности двух выражений равен…
…квадрату первого выражения, минус
удвоенное произведение первого и второго выражений, плюс квадрат второго
выражения.
Закончите формулировку
Слайд 11
Произведение разности двух выражений на их сумму равно…
(a-b)(a+b)=
a2-b2
…разности квадратов
этих выражений.
Закончите формулировку
Слайд 12
Разность квадратов двух выражений равна…
…произведению разности
этих
выражений на их сумму.
Закончите формулировку
Слайд 13
Сумма кубов двух выражений равна…
…произведению суммы этих
выражений и неполного квадрата их разности.
Закончите формулировку
Слайд 14
Разность кубов двух выражений равна…
…произведению разности этих
выражений и неполного квадрата их суммы.
Закончите формулировку
Слайд 18
Замените * так, чтобы выполнялось равенство:
Слайд 19
Найдите ошибки:
(в - у)2 = в -
2ву + у2
(7 + с)2 = 49 -
14с + с2
(р - 10)2 = р2 - 20р + 10
(2а + 1)2 = 4а2 + 2а + 1
2
+
0
4
Слайд 21
Математический диктант
Запишите:
квадрат числа а;
удвоенное число b;
Сумму х и
у:
сумму квадрата х и куба у;
удвоенное произведение а и
b;
утроенное произведение с и d;
квадрат суммы а и b;
квадрат разности х и у;
произведение b и квадрата а;
произведение куба а и удвоенного числа b;
.
Слайд 22
Математический диктант
3.
4.
5.
6.
7.
8.
9.
10.
a2
2b
x + y
x2
+ y3
2ab
3cd
(a + b)2
(x-y)2
b.a2
a3.2b
Слайд 23
Задания пронумерованы буквами, ответы - цифрами. Запишите
по порядку буквы, соответствующие правильным ответам и заданиям.
Кодированный математический
диктант.
Слайд 24
1) (7-у)(7+у)
2) (х-3)3
3) ( а - 5
) (а2 + 5а + 25)
4) a2(а- b)
5) (
x + 2) (х2 - 2х + 4 )
6) 2(у-5)2
7) (7 + у)2
8) ( 2х - 3 )(2х + 3 )
9) (1 - 49а6)
Слайд 25
СМОТРИ, НЕ ОШИБИСЬ!
(х ... у)2 = х2 -
2х + ...
(... - ...)2 = 9х2 ...
... + 25у2
(... ... ...)2 = ... - 28ху ... 49х2
(х - ... )2 = ... ... 20х ... ...
25a2 + … + b2 = (… … …)2
- у y2
3x 5y - 30xy
2y - 7x 4y2 +
10y x2 - у + 100y2
10ab 5a + b
Слайд 26
Упростите выражение:
(а-4)2-2а(За-4)
А) -5а2 + 16;
Б) -5а2 +
8а- 16;
В) -5а2+8;
Г) -5а2 + 8а-4.
Слайд 27
Упростите выражение:
(с + 5)2-с(10-Зс)
А) -2с2+25 ;
Б) 4с2-
10с+ 25;
В) 4с2-5с+ 25;
Г) 4с2 + 25.
Слайд 28
Упростите выражение:
3 (а- 1)2 + 6а
А)
9а2 - 6а + 9;
Б) 3а2+6а -3;
В) 3а2+1;
Г)
3а2+3.
Слайд 29
Упростите выражение:
8х +4 (1 -х )2
А) 4х2
+ 4;
Б) 4 +х2;
В) 4 + 8х2-4х2;
Г)
16х2-24х+ 16.
Слайд 30
Преобразуйте в многочлен выражения:
4с ( с - 2)
- ( с - 4)2
А) 3с2- 16;
Б) 5с2-16;
В) Зс2-
16с -16;
Г) Зс2+ 16.
Слайд 31
Узнайте единение каких континентов символизируют эти кольца. Замените
выражения многочленами стандартного вида.
2
Слайд 33
« В здоровом теле здоровый дух! »
Слайд 34
Расширение знаний по формулам сокращенного умножения
Слайд 35
Цель проекта: научиться возводить в квадрат сумму трёх,
четырёх, и т.д. слагаемых.
(а+в+с+d)2
(а+в+с+d+e)2
(а+в+с)2 (а+в+с+d+ e+k)2
Проект № 1
Слайд 36
(а+b+с+d)2 =
=((a+ b)+(c+ d))2=
=(a+ b)2 +
2(a+ b)(c+ d)+(c+ d)2 =
=a2+ 2ab+ b2+ 2ac+
2ad+ 2bc+ 2bd+ c2+ 2cd+ d2=
=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd
Возводить в квадрат сумму трёх, четырёх, и более слагаемых
Слайд 37
ВЫВОД: квадрат суммы трёх, четырёх и более чисел
равен сумме квадратов каждого из этих чисел плюс удвоенные
произведения каждого из этих чисел на числа, следующие за ним.
(а + b + с + d)2 = a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd
Слайд 38
(3х+4у+5z)2=
=9x2 +16y2 +25z2 +24xy +30xz + 40yz
Вычислите:
Слайд 39
Цель проекта: научиться возводить двучлен в любую натуральную
степень.
Проект № 2
Слайд 40
(а+в)4 =
(a+ b)2(a+ b)2=
= (a2+
2ab+ b2)(a2+ 2ab+ b2)=
=a4+4a3b+ 6a2b2 +4ab3+b4
Слайд 41
(а+b)4 =
=((a+ b)2)2 =
=(
a2+ 2ab+ b2)2=
= а4+4а2b2+b4+4a3b+2a2b2+4ab3 =
= а4 +4a3b+6a2b2+4ab3+b4
Слайд 42
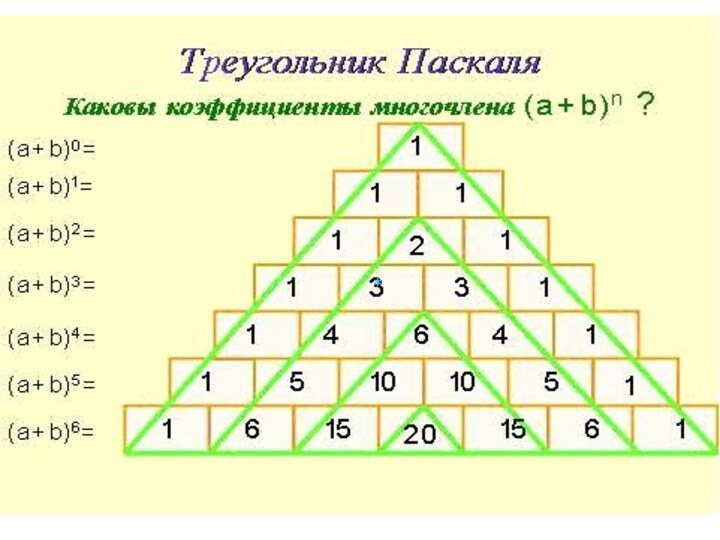
Рассмотрим двучлены:
(а + b)0 = 1
(a +
b)1 = 1a +1 b
(a + b)2 =1 a2
+ 2ab +1 b2
(a + b)3 =1 a3 + 3a2b + 3ab2 + 1b3
Составим таблицу из их коэффициентов:
1
1 1
1 2 1
1 3 3 1
Слайд 44
Блез Паскаль (1623 – 1662)
1 - 20
1
1 - 21
1 2 1 - 22
1 3 3
1 - 23
Слайд 45
При упрощении выражений.
При разложении выражений на множители.
При решении
уравнений.
При доказательстве тождеств.
Где применяются
формулы сокращенного умножения?
Слайд 46
Применяются в некоторых математических фокусах.
Предлагается
кому-нибудь задумать не очень большое число и возвести его
в квадрат. К результату попросите прибавить удвоенное задуманное число и ещё единицу. Выяснив окончательный результат, вы сможете назвать задуманное число. Как найти задуманное число?
формула а2 + 2 а + 1 = (а +1)2
Слайд 47
Домашнее задание
Повторить формулы сокращенного умножения
Постройте треугольник Паскаля
Возведите в
степень (а + b)5
Возводить в квадрат сумму пяти
слагаемых (а+b+с+d +e)2
Подготовиться к контрольной работе.
Слайд 48
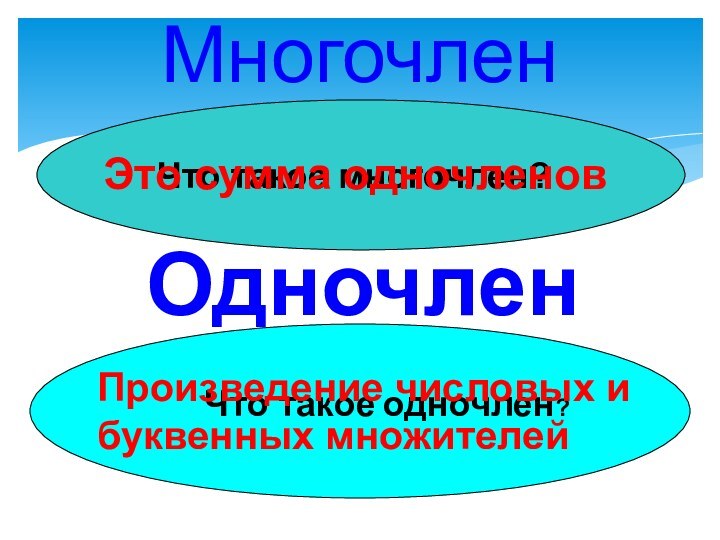
Многочлен
Что такое многочлен?
Это сумма одночленов
Одночлен
Что такое одночлен?
Произведение
числовых и буквенных множителей
Слайд 49
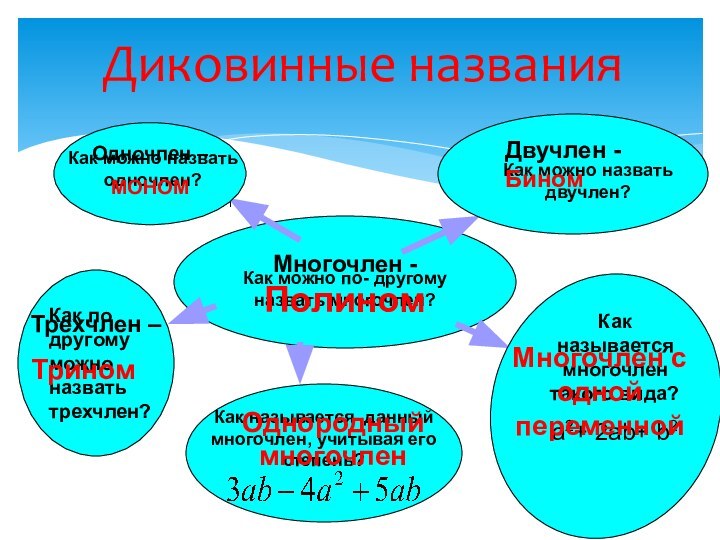
Диковинные названия
Как можно по- другому назвать многочлен?
Многочлен -Полином
Как
можно назвать одночлен?
Одночлен –
МОНОМ
Как можно назвать двучлен?
Двучлен -Бином
Как по
другому можно назвать трехчлен?
Трехчлен –
Трином
Как называется данный многочлен, учитывая его степень?
Однородный многочлен
Как называется многочлен такого вида?
a2+ 2ab+ b2
Многочлен с одной переменной
Слайд 50
Много даёт математика для умственного развития человека –
заставляет думать, соображать, искать простые и красивые решения, помогает
развивать логическое мышление, умение правильно и последовательно рассуждать, тренировать память, внимание, формирует многие учебные навыки.
« Математику уже затем учить следует, что она ум в порядок приводит»
М.В Ломоносов
Слайд 51
Мне очень понравилось, я всё понял,
у меня всё получается
Я узнал новое на уроке
У меня
ничего не получилось
У меня не всё получилось