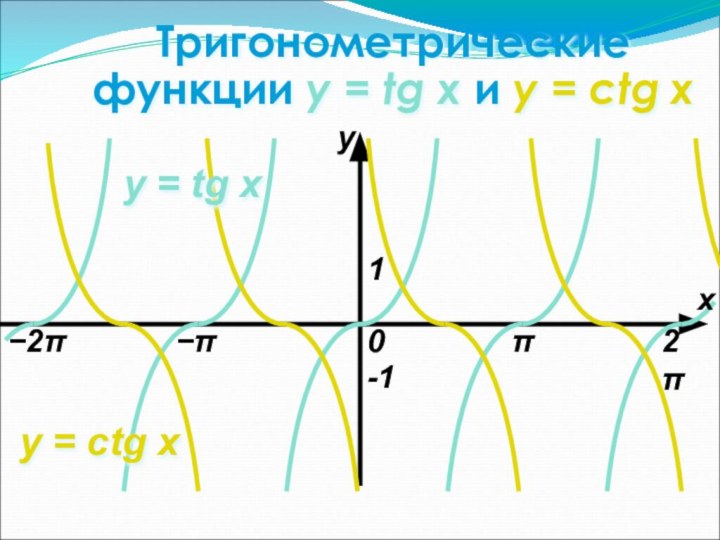
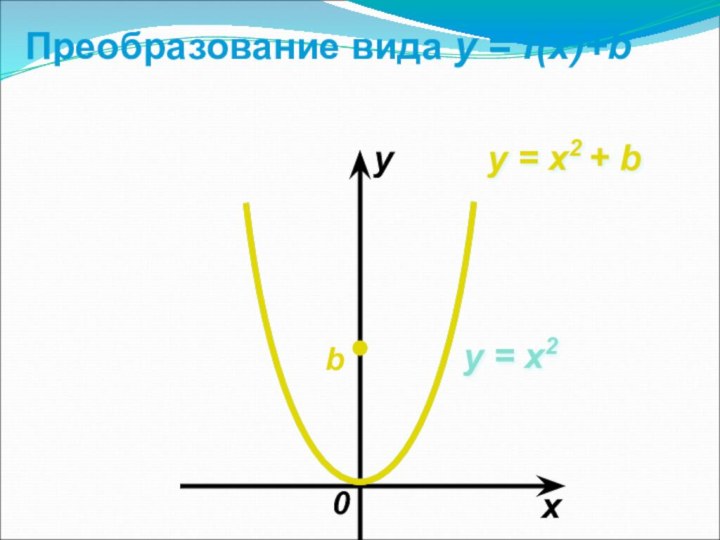
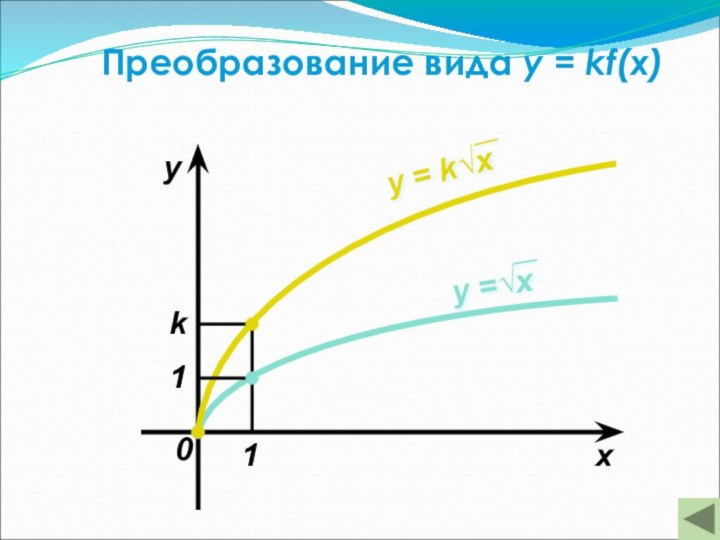
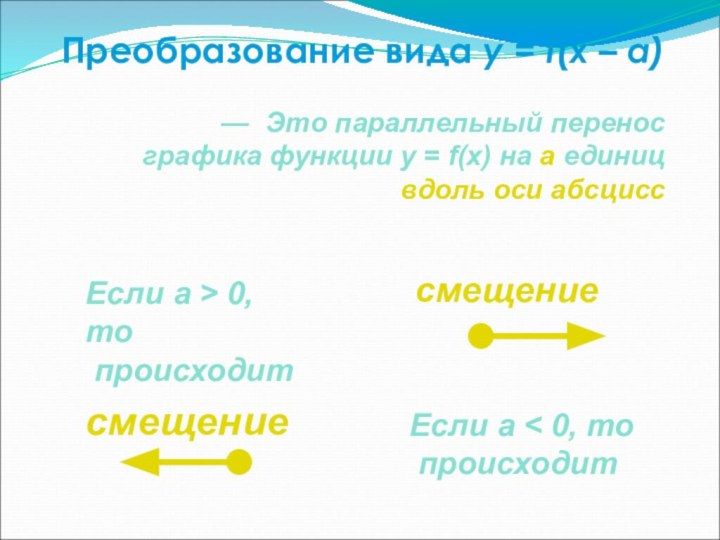
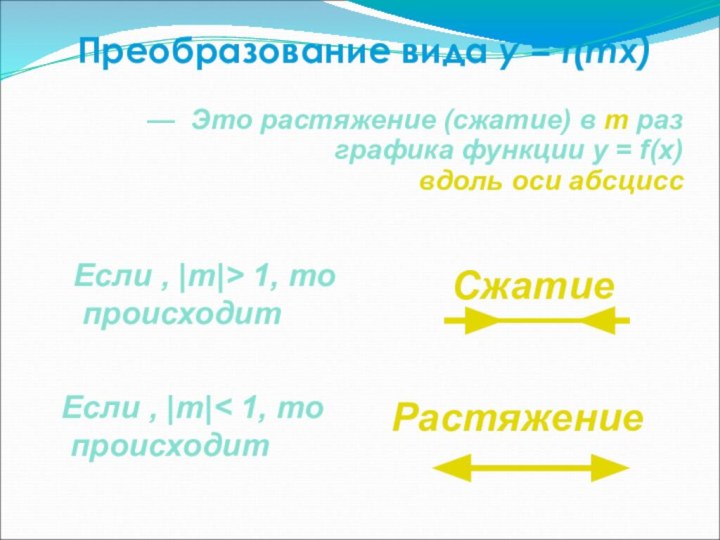
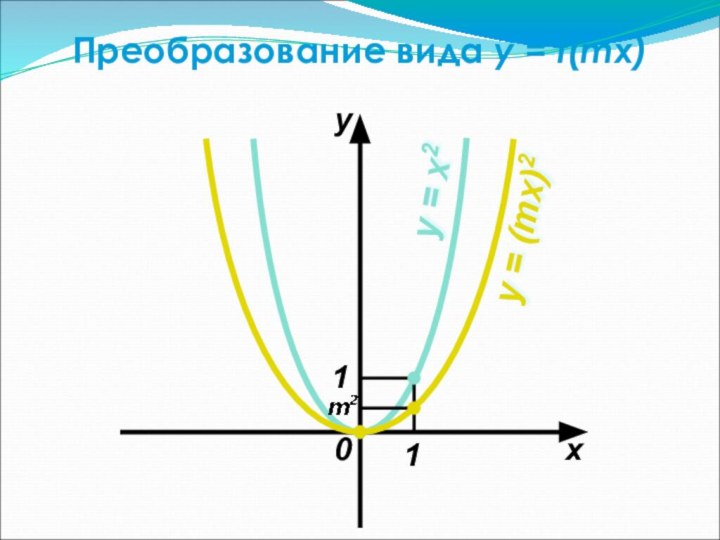
называется соответствие при котором каждому числу x из множества
D сопоставляется по некоторому правилу число y, зависящее от x.x – аргумент функции (независимая переменная)
Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f(x)














![Презентация по математике на тему Функции.Способы ее задания. Преобразования графиков Свойства функции y = sin x1о D(y)=(−∞; +∞). 2о E(y)=[−1; 1]. 3о](/img/tmb/6/554838/3eda1a420feb23a1613711753125cdda-720x.jpg)
![Презентация по математике на тему Функции.Способы ее задания. Преобразования графиков Свойства функции y = cos x1о D(y)=(−∞; +∞). 2о E(y)=[−1; 1]. 3о](/img/tmb/6/554838/ffe26a594898f76650505aa0e9bbcf2d-720x.jpg)