- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгебра и начала анализа
Содержание
- 2. Эпиграф к уроку.Красота в единстве теории и практики.
- 3. Цели обучения, воспитания и развития.Рациональные способы построения
- 4. Задача1.Изобразить в координатной плоскости ХОУ заданные соотношения
- 5. Способ первый.Первый способ построения графика функции –
- 6. Алгоритм построения. у1 = х –прямая –
- 7. Демонстрация алгоритма построения.
- 8. Способ второй.Второй способ построения графика функции –
- 9. Алгоритм построенияЕсли
- 10. В построенном графике – прямой
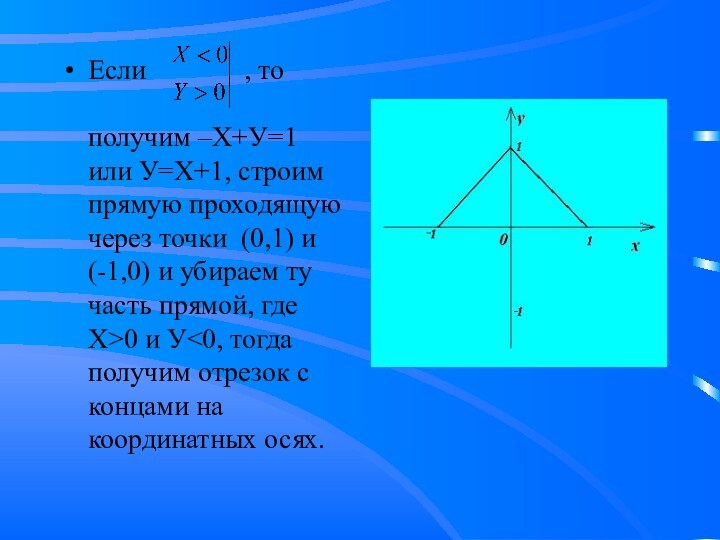
- 11. Если
- 12. Аналогично построим графики - прямые в третьей
- 13. Скачать презентацию
- 14. Похожие презентации
Эпиграф к уроку.Красота в единстве теории и практики.











Слайд 3
Цели обучения, воспитания и развития.
Рациональные способы построения графиков
функций.
решению задач алгебры.
Слайд 4
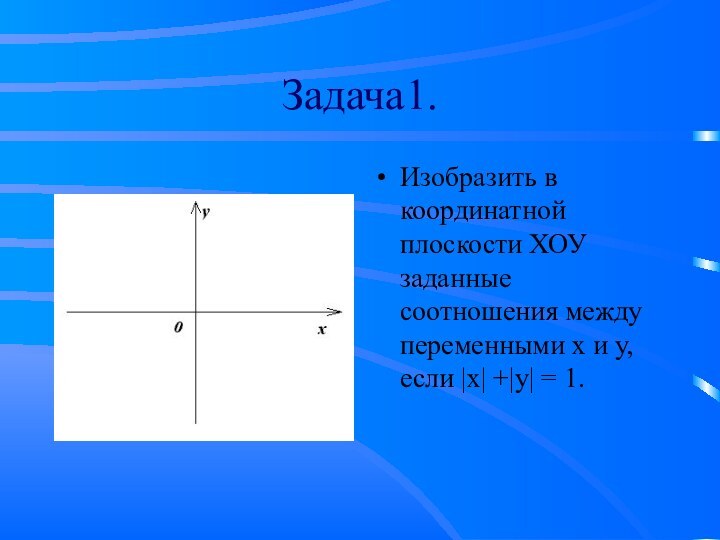
Задача1.
Изобразить в координатной плоскости ХОУ заданные соотношения между
переменными х и у, если |x| +|y| = 1.
Слайд 5
Способ первый.
Первый способ построения графика функции – это
построение требуемого графика путем преобразований на координатной плоскости.
Данная функция
|x|+|y|=1.Выразим у через х;
|y|=-|x|+1.
Далее составим алгоритм построения графика функции |y|=-|x|+1.
Слайд 6
Алгоритм построения.
у1 = х –прямая – биссектриса
1 и 3 четверти координатной плоскости.
у2 = |x|
– строим путем отображения графика функции у1 относительно оси (ох) в верхнюю полуплоскость.у3 = -|x| – отображаем график функции у2 относительно оси (ох) в нижнюю полуплоскость.
у4 = -|x| + 1 –параллельный перенос графика функции у3 по оси (оу) на 1 вверх.
|y| = -|x| + 1 –отбрасываем часть графика у4 в нижней полуплоскости и оставшуюся часть отображаем относительно оси (ох) в нижнюю полуплоскость, тогда получим требуемый график заданной функции |y| + |x| = 1.
Слайд 8
Способ второй.
Второй способ построения графика функции – это
раскрытие модулей в четвертях координатной плоскости с учётом знаков
координатных осей.





























