- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Решение тригонометрических уравнений с отбором корней
Содержание
- 2. Содержание Метод замены переменной Метод разложения на
- 3. Метод замены переменнойС помощью замены t =
- 4. Метод разложения на множителиСуть этого метода заключается
- 5. Однородные тригонометрические уравненияУравнение вида a sin x
- 6. Однородные тригонометрические уравненияa sin2x + b sin
- 7. С помощью тригонометрических формул1. Формулы сложения:sin (x
- 8. С помощью тригонометрических формул2. Формулы приведения:
- 9. Лошадиное правилоВ старые добрые времена жил рассеянный
- 10. С помощью тригонометрических формул3. Формулы двойного аргумента:
- 12. Задания из открытого банка
- 13. Скачать презентацию
- 14. Похожие презентации
Содержание Метод замены переменной Метод разложения на множителиОднородные тригонометрические уравненияС помощью тригонометрических формул:Формул сложенияФормул приведенияФормул двойного аргумента












Слайд 2
Содержание
Метод замены переменной
Метод разложения на множители
Однородные
тригонометрические уравнения
Слайд 3
Метод замены переменной
С помощью замены t = sinx
или t = cosx, где t ∈ [−1;1] решение
исходного уравнения сводится к решению квадратного или другого алгебраического уравнения
Слайд 4
Метод разложения на множители
Суть этого метода заключается в
том, что произведение нескольких множителей равно нулю, если хотя
бы один из них равен нулю, а другие при этом не теряют смысл:f(x) · g(x) · h(x) · … = 0 ⟺ f(x) = 0 или g(x) = 0 или h(x) = 0
и т.д. при условии существования каждого из сомножителей
Слайд 5
Однородные тригонометрические уравнения
Уравнение вида a sin x +
b cos x = 0 называют однородным тригонометрическим уравнением
первой степени.a sin x + b cos x = 0
Замечание.
Деление на cos x допустимо, поскольку решения уравнения cos x = 0 не являются решениями уравнения a sin x + b cos x = 0.
: cos x
a tg x + b = 0
Слайд 6
Однородные тригонометрические уравнения
a sin2x + b sin x
cos x + c cos2x = 0
Уравнение вида a
sin2x + b sin x cos x + c cos2x = 0 называют однородным тригонометрическим уравнением второй степени.: cos2x
a tg2x + b tg x + c = 0
Далее, вводим новую переменную tg x = t и решаем методом замены переменной.
Замечание. Если в данном уравнении а = 0 или с = 0 то, уравнение решается методом разложения
на множители.
Слайд 7
С помощью тригонометрических формул
1. Формулы сложения:
sin (x +
y) = sinx cosy + cosx siny
cos (x +
y) = cosx cosy − sinx sinysin (x − y) = sinx cosy + cosx siny
cos (x − y) = cosx cosy + sinx siny
Слайд 9
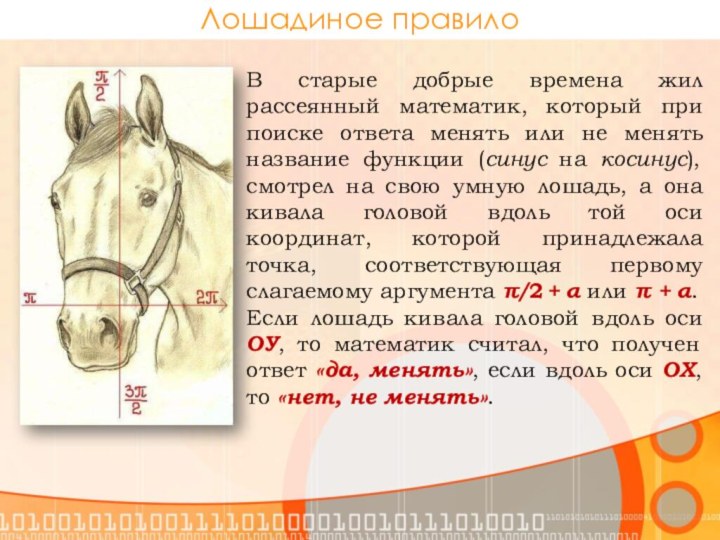
Лошадиное правило
В старые добрые времена жил рассеянный математик,
который при поиске ответа менять или не менять название
функции (синус на косинус), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/ 2 + α или π + α.Если лошадь кивала головой вдоль оси ОУ, то математик считал, что получен ответ «да, менять», если вдоль оси ОХ, то «нет, не менять».
Слайд 10
С помощью тригонометрических формул
3. Формулы двойного аргумента:
sin 2x = 2sinx cosx
cos 2x = cos2x –
sin2xcos 2x = 2cos2x – 1
cos 2x = 1 – 2sin2x