подготовить их к оперативному контролю.
2.Способствовать развитию познавательного интереса к
предмету.3.Воспитывать самостоятельность, аккуратность, чёткость в действиях.
Форма организации деятельности: фронтальная, самостоятельная работа обучающего характера, работа в парах.
Оборудование:
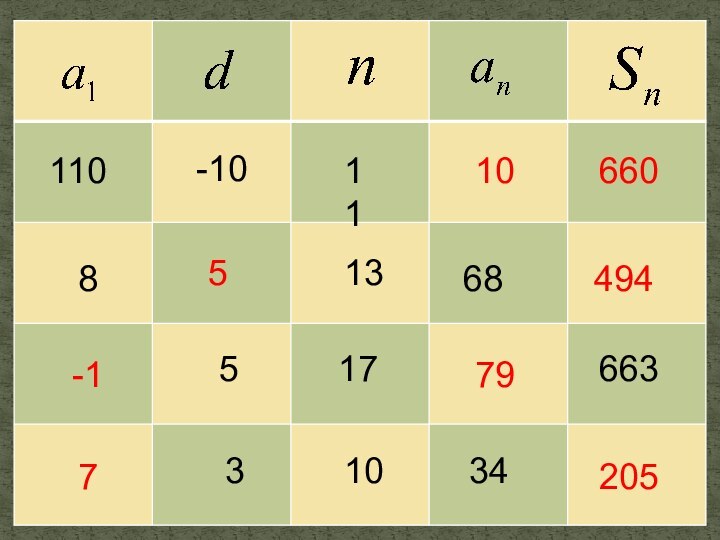
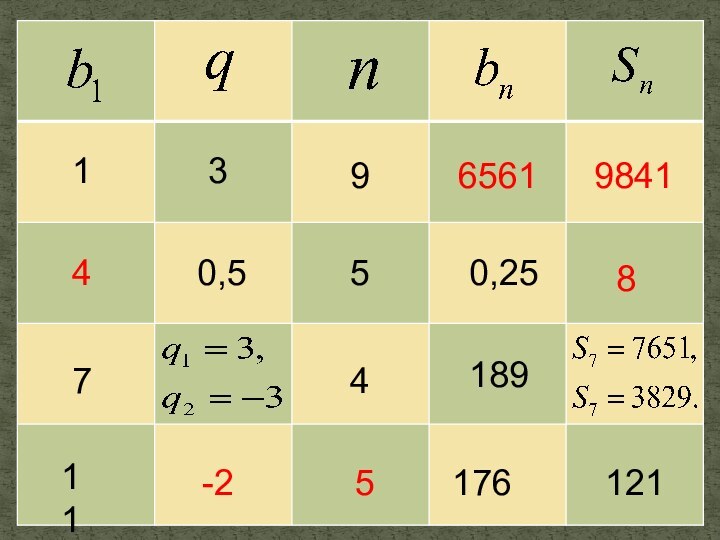
презентация «Арифметическая и геометрическая прогрессии»
«Учись у всех, не подражай никому!»
(М.Горький)