- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Конференция по истории математики на тему Математика переменных величин
Содержание
- 3. При изучении истории любой науки можно проследить
- 4. Андрей Николаевич Колмогоров (1903-1987), русский математик. В
- 5. I период
- 6. Предпосылки возникновения и развития математики переменных величин
- 7. Период элементарной математики заканчивается, когда центр тяжести математических интересов переносится в область математики переменных величин.
- 8. На первый план выдвигается понятие функции, играющее
- 9. Первое знакомство европейских учёных с античными открытиями
- 10. XVI век стал переломным для европейской математики.
- 11. Одновременно растёт престиж математики, в изобилии появляется
- 12. ДЕКАРТ РЕНЕ (1596-1650)
- 13. Рене Декарт – французский математик, философ, физик,
- 14. Уделял большое внимание Декарт и занятиям математикой,
- 15. Ученый являлся первым, кто ввел коэффициенты, переменные
- 16. Ньютон Исаак (1643-1727 гг.)
- 17. Английский математик, физик, алхимик и историк. Родился
- 18. «Универсальная арифметика» Ньютона, латинское издание
- 19. Приходится признать, что терминология и символика Ньютона
- 20. Лейбниц Готфрид Вильгельм (1646— 1710 гг.)
- 21. Немецкий философ. Родился в Лейпциге. Интересы Лейбница
- 22. Его ум видел истину,Его сердце познало справедливость.Он — гордость ШвейцарииИ всего человечества.
- 23. Семья Бернулли была родом из Антверпена, но
- 25. Иога́нн Бернулли — швейцарский математик, механик, врач и
- 26. 1691: будучи во Франции, пропагандирует новое исчисление,
- 27. 1696: Иоганн публикует задачу о брахистохроне: найти
- 28. 1699: вместе с Якобом избран иностранным членом
- 29. Я́коб Берну́лли (1655-1705)
- 30. Один из основателей теории вероятностей и математического
- 31. Якобу Бернулли принадлежат значительные достижения в теории
- 32. Леонард Эйлер (1707-1783)
- 33. Леона́рд Э́йлер ( 15 апреля 1707, Базель, Швейцария —
- 34. Леонард Эйлер родился в 1707 году в
- 35. Посещая дом своего учителя, Эйлер познакомился и
- 36. Эйлер активно трудился до последних дней. В
- 37. Скачать презентацию
- 38. Похожие презентации


































Слайд 3
При изучении истории любой науки можно
проследить развитие
(генезис) идей, как они
их облекали учёные. Каждому учёному приходится, занимаясь какой-либо наукой, изучать её историю, чтобы понять какое место в этой науке занимают его исследования и открытия, а также чтобы «заново не изобретать велосипед». Кроме того, при неожиданных открытиях в истории науки удаётся удлинить её прошлое и память человечества.
Слайд 4
Андрей Николаевич Колмогоров (1903-1987), русский математик.
В периодизации истории
математики, которую дал академик А.Н.Колмагоров, выделяются следующие периоды:
1) период
зарождения математики до VI-V века до н.э.
2) математика постоянных величин до XVII века н.э. (внутри этого периода отдельно выделяется арабская математика с IX по XV в.н.э.)
3)математика переменных величин с XVII –до середины XIX в.н.э.
4) современная математика с середины XIX в.н.э.Слайд 5 I период
!
II период - элементарная математика ! III период ! IVпериод! (наука основана на доказательстве – ! матем. перем величин ! совр. матем
! дедуктивная математика) ! !
Зарождение математики! Математика пост. величин ! !
__________________VI-Vв. до н.э. ______0________________XVI-XVII в____________2 полов________
XIXв
Слайд 7 Период элементарной математики заканчивается, когда центр тяжести математических
интересов переносится в область математики переменных величин.
Слайд 8 На первый план выдвигается понятие функции, играющее в
дальнейшем такую же роль основного и самостоятельного предмета изучения,
как ранее понятия величины или числа. Изучение переменных величин и функциональных зависимостей приводит далее к основным понятиям математического анализа, вводящим в математике в явном виде идею бесконечного, к понятиям предела, производной, дифференциала и интеграла, созданию аналитический геометрии. Наряду с уравнениями, в которых неизвестными являются числа, появляются уравнения, в которых неизвестны и подлежат определению функции.Слайд 9 Первое знакомство европейских учёных с античными открытиями происходило
в Испании. В XII веке там переводятся (с греческого
и арабского на латинский) основные труды великих греков и их исламских учеников. Интерес к науке растёт, и одно из проявлений этого — смена числовой системы. Долгое время в Европе применялись римские цифры. В XII—XIII веках публикуются первые в Европе изложения десятичной позиционной системы записи (сначала переводы ал-Хорезми, потом собственные руководства), и начинается её применение. С XIV века индо-арабские цифры начинают вытеснять римские даже на могильных плитах.
)
Латинский перевод «Начал» Евклида (XIV век
Слайд 10 XVI век стал переломным для европейской математики. Полностью
усвоив достижения предшественников, она несколькими мощными рывками вырвалась далеко
вперёд.Первым крупным достижением стало открытие общего метода решения уравнений третьей и четвёртой степени. Итальянские математики дель Ферро, Тарталья и Феррари решили проблему, с которой несколько веков не могли справиться лучшие математики мира. При этом обнаружилось, что в решении иногда появлялись «невозможные» корни из отрицательных чисел. После анализа ситуации европейские математики назвали эти корни «мнимыми числами» и выработали правила обращения с ними, приводящие к правильному результату. Так в математику впервые вошли комплексные числа.
Важнейший шаг к новой математике сделал француз Франсуа Виет. Он окончательно сформулировал символический метаязык арифметики — буквенную алгебу.
Третье великое открытие XVI века — изобретение логарифмов (Джон Непер). В 1585 году фламандец Симон Стевин издаёт книгу «Десятая» о правилах действий с десятичными дробями, после чего десятичная система одерживает окончательную победу и в области дробных чисел.
Джон Непер
Слайд 11 Одновременно растёт престиж математики, в изобилии появляется множество
практических задач, требующих решения — в артиллерии, мореплавании, строительстве, промышленности,
гидравлике, астрономии, картографии, оптике и др. И, в отличие от античности, учёные Возрождения не чурались таких задач. Чистых математиков-теоретиков фактически не было. Появляются первые Академии наук. В XVI—XVII веках роль университетской науки падает, появляется множество учёных-непрофессионалов: Стевин — военный инженер, Виет и Ферма — юристы, Дезарг и Рен — архитекторы, Лейбниц — чиновник, Непер, Декарт, Паскаль — частные лицаМатематики XVI века, средневековая миниатюра
Слайд 13 Рене Декарт – французский математик, философ, физик, физиолог,
авторитетнейший метафизик Нового времени, ученый, заложивший основы аналитической геометрии,
современной алгебраической символики, новоевропейского рационализма. Декарт, родившийся 31 марта 1596 г. в г. Лаэ французской провинции Турень, был сыном советника, потомком обедневшего дворянского рода де Карт, давшего впоследствии название картезианству – философскому направлению.Окончив иезуитскую школу, он поступил в университет Пуатье, где в 1616 г. им была получена степень бакалавра права. В следующем году Декарт подался в военнослужащие и побывал во многих местах Европы.
Вольнолюбие Декарта не ускользнуло от внимания иезуитов, которые выдвинули ему обвинение в ереси. В 1628 г. опальный ученый на два десятка лет покидает родную Францию, переехав в Голландию. В этой стране он не имел постоянного места жительства, переезжая из одного города в другой. Первая книга программного содержания, «Мир», была написана в 1634 г., но ученый принял решение не издавать ее: на слуху у всех был Галилей, который чуть было не стал жертвой инквизиции. В 1637 г. увидело свет его сочинение «Рассуждение о методе», которую многие исследователи считают стартом новоевропейской философии.
«Сомневаюсь, следовательно, существую» - истина, сформулированная Рене Декартом, которая сделала значительный поворот европейской философии Нового времени. Основой любой мысли является сознание, поэтому ученый отрицает любое проявление бессознательного мышления. Идея – это настоящее свойство души, поэтому она является «мыслящей вещью».
Слайд 14 Уделял большое внимание Декарт и занятиям математикой, которые
также сыграли огромную роль в развитии этой науки. В
1637 г. увидел свет его труд «Геометрия»; с введением нового метода координат о нем стали говорить как об основателе аналитической геометрии.Труды Декарта издавались во Франции благодаря благосклонности кардинала Ришелье, но голландскими богословами они были осуждены. Вконец устав от долгих лет травли, ученый ответил согласием на приглашение королевы Швеции Кристины, с которой его связывала многолетняя переписка, и в 1649 г. переехал в Стокгольм. Жесткий график (чтобы выполнять поручения монаршей персоны, преподавать ей, ему приходилось подниматься в пять утра), холодный климат привели к тому, что он сильно простудился и скончался 11 февраля в 1650 г. от пневмонии. Есть версия, связывающая смерть Декарта с отравлением мышьяком: якобы на преступление пошли силы, опасавшиеся, что под влиянием свободолюбивого наставника Кристина не станет католичкой.
Слайд 15 Ученый являлся первым, кто ввел коэффициенты, переменные величины,
а также обозначения степеней. Внес свой вклад в теорию
уравнений: сформулировал правило знаков для нахождения числа отрицательных и положительных корней. Также показал, что уравнение третьей степени можно решить в квадратных радикалах или же с помощью линейки и циркуля.Вместе с Пьером Ферма стал автором аналитической геометрии. Данная наука позволила алгебраизировать геометрию и рассматривать ее с помощью координатного метода. Предложенная им координатная система названа в честь ученого.
В 1637 году Декарт написал пособие «Геометрия», в котором и рассказал о взаимодействии алгебры и геометрии. Здесь впервые рассматривались такие понятия, как функция и переменное значение.
Также в эту работу были включены линии, которые описывают при своем движении шарнирные механизмы. Исследуя линзы, ученый изложил основные методы построения касательных и нормалей к плоским кривым.
В настоящее время всему миру известно, что открыл Рене Декарт. Его работа «Геометрия» повлияла на развитие всех направлений математических наук. Благодаря изобретенной им системе координат, получилось реально истолковать происхождение отрицательного числа
Слайд 17
Английский математик, физик, алхимик и историк. Родился в
семье фермера.
В12 лет поступил в Грантемскую школу, в 1661
г — в колледж Св. Троицы (Тринити-колледж) Кембриджского университета.Окончив университет, Ньютон в 1665 г получил ученую степень бакалавра. В 1665-1667 гг. у него сложились в основном те идеи, которые привели его к созданию дифференциального и интегрального исчислений, изобретению зеркального телескопа, открытию закона всемирного тяготения.В Кембридже он провел и опыты над разложением света. В 1668 г. Ньютону была присвоена степень магистра. В 1671 г. Ньютон построил второй зеркальный телескоп — больших размеров и лучшего качества. Ньютону принадлежат обоснованные тончайшими экспериментами представления о монохроматических световых лучах и периодичности их свойств, лежащие в основе физической оптики.
В 1687 г. Ньютон опубликовал свой грандиозный труд «Математические начала натуральной философии» (кратко — «Начала»), заложивший основы не только рациональной механики, но и всего математического естествознания. «Начала» содержали законы динамики, закон всемирного тяготения с эффективными приложениями к движению небесных тел, истоки учения о движении и сопротивлении жидкостей и газов, включая акустику.
В 1705 г. за научные труды королева Анна возвела его в рыцарское звание. В последние годы жизни Ньютон много времени посвящал теологии и античной и библейской истории. Похоронен Ньютон в английском национальном пантеоне —Вестминстерском аббатстве.
Слайд 18
«Универсальная арифметика» Ньютона, латинское издание (1707)
Первые
математические открытия Ньютон сделал ещё в студенческие годы: классификация
алгебраических кривых 3-го порядка и биномиальное разложение произвольной (не обязательно целой) степени, с которого начинается ньютоновская теория бесконечных рядов — нового и мощнейшего инструмента анализа. Ньютон разработал дифференциальное и интегральное исчисление одновременно с Г. Лейбницем (немного раньше) и независимо от него. Уже будучи студентом, Ньютон понял, что дифференцирование и интегрирование — взаимно обратные операции]. Эта основная теорема анализа уже более или менее ясно вырисовывалась в работах Торричелли, Грегори и Барроу, однако лишь Ньютон понял, что на этой основе можно получить не только отдельные открытия, но мощное системное исчисление, подобное алгебре, с чёткими правилами и гигантскими возможностями.Ньютон почти 30 лет не заботился о публикации своего варианта анализа, хотя в письмах (в частности, к Лейбницу) охотно делится многим из достигнутого. Тем временем вариант Лейбница широко и открыто распространяется по Европе с 1676 года. Лишь в 1693 году появляется первое изложение варианта Ньютона — в виде приложения к «Трактату по алгебре» Валлиса].
Слайд 19 Приходится признать, что терминология и символика Ньютона по
сравнению с лейбницевской довольно неуклюжи: флюксия (производная), флюэнта (первообразная),
момент величины (дифференциал) и т. п. Сохранились в математике только ньютоновское обозначение «o» для бесконечно малой dt (впрочем, эту букву в том же смысле использовал ранее Грегори), да ещё точка над буквой как символ производной по времени.Достаточно полное изложение принципов анализа Ньютон опубликовал только в работе «О квадратуре кривых» (1704), приложенной к его монографии «Оптика». Почти весь изложенный материал был готов ещё в 1670—1680-е годы, но лишь теперь Грегори и Галлей уговорили Ньютона издать работу, которая, с опозданием на 40 лет, стала первым печатным трудом Ньютона по анализу. Здесь у Ньютона появляются производные высших порядков, найдены значения интегралов разнообразных рациональных и иррациональных функций, приведены примеры решения дифференциальных уравнений 1-го порядка.
Слайд 21 Немецкий философ. Родился в Лейпциге. Интересы Лейбница были многогранны:
помимо философии, он оставил серьезный след в логике, математике
и физике (независимо от Ньютона разработал дифференциальное и интегральное исчисление), занимался юриспруденцией, историей и языкознанием.Юридическое образование получил в Лейпцигском университете, философское — в Йенском и Парижском. Свои сочинения писал на немецком и французском языках. Являлся членом Лондонского Королевского общества, Парижской Академии наук, Академии естествознания в Риме, в 1700 г. стал основателем и первым президентом Берлинской Академии наук. Рассматривая известный постулат английского эмпиризма — «Нет ничего в разуме, чего не было бы прежде в чувствах», — Лейбниц дополняет его принципиальным положением: «кроме самого разума». Такой подход позволял уделять большое внимание возможному знанию, что соответствовало и его онтологическим приоритетам. Не удивительно поэтому, что он выступил разработчиком теории вероятностей и теории игр, а в работе «Об искусстве комбинаторики» предвосхитил некоторые положения современной математической логики.
Копия механического калькулятора Лейбница в Немецком музее
Слайд 22
Его ум видел истину,
Его
сердце познало справедливость.
Он — гордость Швейцарии
И всего человечества.
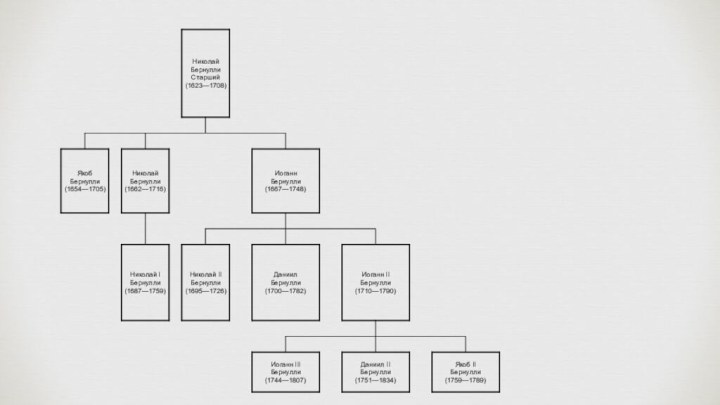
Слайд 23 Семья Бернулли была родом из Антверпена, но им
пришлось уйти в изгнание в 1583 году из-за религиозных
гонений, начатых испанцами в Нидерландах. Совершив остановку во Франкфурте, в 1622 году семья обосновалась в Базеле, Швейцария. Николай Бернулли, как его дед и прадед, был купцом и очень хотел, чтобы его дети занимались богословием, правом или торговлей, иными словами, любым делом, которое приносило бы доход. Однако их увлечение математикой, которое иногда приходилось скрывать от отца, не позволило его планам сбыться. Нельзя сказать, чтобы кто-либо из потомков решил пойти по стопам отца: многие из них изучали дисциплины, далекие от математики, но рано или поздно все равно посвящали себя этой науке.Слайд 25 Иога́нн Бернулли — швейцарский математик, механик, врач и филолог-классицист,
самый знаменитый представитель семейства Бернулли, младший брат Якоба Бернулли,
отец Даниила Бернулли.Один из первых разработчиков математического анализа, после смерти Ньютона — лидер европейских математиков. Учитель Эйлера. Иностранный член Парижской (1699), Берлинской (1701), Петербургской (1725) академий наук и Лондонского Королевского общества (1712).
Иоганн стал магистром (искусств) в 18 лет, перешёл на изучение медицины, но одновременно увлёкся математикой (хотя медицину не бросил, по окончании университета всю жизнь занимался врачебной практикой). Вместе с братом Якобом изучает первые статьи Лейбница о методах дифференциального и интегрального исчисления, начинает собственные глубокие исследования.
Слайд 26 1691: будучи во Франции, пропагандирует новое исчисление, создав
первую парижскую школу анализа. По возвращении в Швейцарию переписывается
со своим учеником маркизом де Лопиталем, которому оставил содержательный конспект нового учения из двух частей: исчисление бесконечно малых и интегральное исчисление.1694: защитил докторскую диссертацию по медицине, женился. У него родились 5 сыновей и 4 дочери.
В ответ на письмо Лопиталя сообщает ему метод раскрытия неопределённостей, известный сейчас как «правило Лопиталя».
Печатает в Acta Eruditorum статью «Общий способ построения всех дифференциальных уравнений первого порядка». Здесь появились выражения «порядок уравнения» и «разделение переменных».
1696: Лопиталь выпускает в Париже под своим именем первый в истории учебник по математическому анализу: «Анализ бесконечно малых для исследования кривых линий» (на французском языке), в основу которого была положена первая часть конспекта Бернулли.
Значение этой книги для распространения нового учения трудно переоценить — не только потому, что она была первой, но и благодаря ясному изложению, прекрасному слогу, обилию примеров.
Гийом Лопиталь
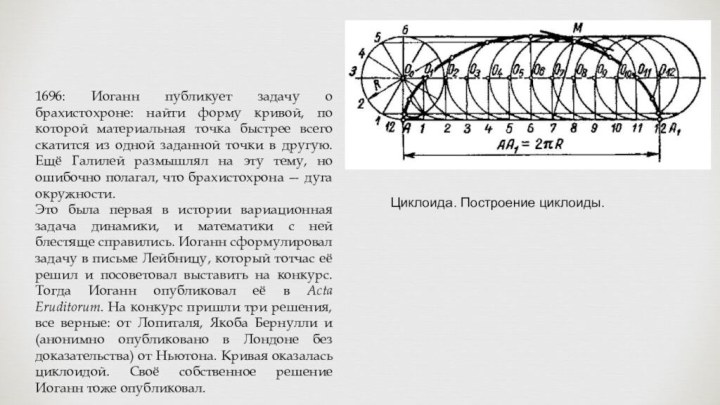
Слайд 27 1696: Иоганн публикует задачу о брахистохроне: найти форму
кривой, по которой материальная точка быстрее всего скатится из
одной заданной точки в другую. Ещё Галилей размышлял на эту тему, но ошибочно полагал, что брахистохрона — дуга окружности.Это была первая в истории вариационная задача динамики, и математики с ней блестяще справились. Иоганн сформулировал задачу в письме Лейбницу, который тотчас её решил и посоветовал выставить на конкурс. Тогда Иоганн опубликовал её в Acta Eruditorum. На конкурс пришли три решения, все верные: от Лопиталя, Якоба Бернулли и (анонимно опубликовано в Лондоне без доказательства) от Ньютона. Кривая оказалась циклоидой. Своё собственное решение Иоганн тоже опубликовал.
Циклоида. Построение циклоиды.
Слайд 28 1699: вместе с Якобом избран иностранным членом Парижской
Академии наук.
1702: совместно с Лейбницем открыл приём разложения рациональных
дробей (под интегралом) на сумму простейших.1705: вернулся в Базельский университет, профессором греческого языка. Восемь раз был избран деканом факультета философии, и дважды — ректором университета. Сразу после смерти брата Якоба (1705) Иоганн был приглашён на его кафедру в Базеле и занимал её до самой смерти (1748).
В честь Якоба и Иоганна Бернулли назван кратер на Луне.
Город на Рейне - Базель
Слайд 30 Один из основателей теории вероятностей и математического анализа.
Старший брат Иоганна Бернулли, совместно с ним положил начало
вариационному исчислению. Доказал частный случай закона больших чисел — теорему Бернулли. Профессор математики Базельского университета (с 1687 года). Иностранный член Парижской академии наук (1699) и Берлинской академии наук (1702).Якоб Бернулли внёс огромный вклад в развитие аналитической геометрии и зарождение вариационного исчисления. Его именем названа лемниската Бернулли. Он исследовал также циклоиду, цепную линию, и особенно логарифмическую спираль. Последнюю из перечисленных кривых Якоб завещал нарисовать на своей могиле; по невежеству там изобразили спираль Архимеда, см. фотографию справа. Согласно завещанию, вокруг спирали выгравирована надпись на латыни, «EADEM MUTATA RESURGO» («изменённая, я вновь воскресаю»), которая отражает свойство логарифмической спирали восстанавливать свою форму после различных преобразований.
Эпитафия и спираль
на гробнице Якоба Бернулли
Слайд 31 Якобу Бернулли принадлежат значительные достижения в теории рядов,
дифференциальном исчислении, теории вероятностей и теории чисел, где его
именем названы «числа Бернулли». Он изучил теорию вероятностей по книге Гюйгенса «О расчётах в азартной игре», в которой ещё не было определения и понятия вероятности (её заменяет количество благоприятных случаев). Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей и сформулировал первый вариант закона больших чисел. Якоб Бернулли подготовил монографию в этой области, однако издать её не успел. Она была напечатана посмертно, в 1713 году, его братом Николаем, под названием «Искусство предположений» (Ars conjectandi). Это содержательный трактат по теории вероятностей, статистике и их практическому применению, итог комбинаторики и теории вероятностей XVII века. Имя Якоба носит важное в комбинаторике распределение Бернулли.
«Искусство предположений»
Слайд 33
Леона́рд Э́йлер ( 15 апреля 1707, Базель, Швейцария — 7
сентября 1783, Санкт-Петербург, Российская империя) — швейцарский, немецкий и российский
математик и механик, внёсший фундаментальный вклад в развитие этих наук (а также физики, астрономии и ряда прикладных наук). Эйлер — автор более чем 850 работ (включая два десятка фундаментальных монографий) по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям. Он глубоко изучал медицину, химию, ботанику, воздухоплавание, теорию музыки, множество европейских и древних языков. Академик Петербургской, Берлинской, Туринской, Лиссабонской и Базельской академий наук, иностранный член Парижской академии наук.Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. В 1726 году он был приглашён работать в Санкт-Петербург, куда переехал годом позже. С 1726 по 1741, а также с 1766 года был академиком Петербургской академии наук (будучи сначала адъюнктом, а с 1731 года — профессором); в 1741—1766 годах работал в Берлине (оставаясь одновременно почётным членом Петербургской академии). Уже через год пребывания в России он хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики-математики (С. К. Котельников) и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России
Работа
Слайд 34 Леонард Эйлер родился в 1707 году в семье
базельского пастора Пауля Эйлера, друга семьи Бернулли, и Маргариты
Эйлер, урождённой Брукер. Начальное обучение Леонард получил дома под руководством отца (тот в своё время учился математике у Якоба Бернулли). Пастор готовил старшего сына к духовной карьере, однако занимался с ним и математикой — как в качестве развлечения, так и для развития логического мышления, и Леонард рано проявил математические способности.Когда Леонард подрос, его перевезли к бабушке в Базель, где он учился в гимназии (продолжая при этом увлечённо изучать математику). В 1720 году способного гимназиста допустили к посещению публичных лекций в Базельском университете; там он обратил на себя внимание профессора Иоганна Бернулли (младшего брата Якоба Бернулли). Знаменитый учёный передал одарённому подростку для изучения математические статьи, разрешив при этом для прояснения трудных мест приходить к нему домой по субботам после обеда
Слайд 35 Посещая дом своего учителя, Эйлер познакомился и подружился
с его сыновьями — Даниилом и Николаем, которые также, по
семейной традиции, глубоко изучали математику. Надо отметить, что число научных вакансий в Швейцарии было совсем невелико. Поэтому братья Даниил и Николай Бернулли уехали в Россию, где как раз шла организация Академии наук; они обещали похлопотать там и о должности для Эйлера].В начале зимы 1726—1727 гг. Эйлер получил известие из Санкт-Петербурга: по рекомендации братьев Бернулли он приглашён на должность адъюнкта (помощника профессора) по кафедре физиологии.Поскольку Иоганн Бернулли был известным врачом, то в России считали, что Леонард Эйлер как его лучший ученик — тоже врач. Свой отъезд из Базеля Эйлер отложил, однако, до весны, посвятив оставшиеся месяцы серьёзному изучению медицинских наук, глубоким знанием которых он впоследствии поражал своих современников. Наконец, 5 апреля 1727 года Эйлер навсегда покинул Швейцарию, хотя швейцарское подданство сохранил до конца жизни.
27 декабря 1733 года 26-летний Леонард Эйлер женился на своей ровеснице Катарине , дочери академического живописца Георга Гзеля (петербургского швейцарца). Молодожёны приобрели дом на набережной Невы, где и поселились. В семье Эйлера родились 13 детей, но выжили 3 сына и 2 дочери
Слайд 36 Эйлер активно трудился до последних дней. В сентябре
1783 года 76-летний учёный стал ощущать головные боли и
слабость. 7 сентября после обеда, проведённого в кругу семьи, беседуя с академиком А. И. Лекселем о недавно открытой планете Уран и её орбите, он внезапно почувствовал себя плохо. Эйлер успел произнести: «Я умираю», — и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг.«Он перестал вычислять и жить», — сказал Кондорсе на траурном заседании Парижской Академии наук.
Его похоронили на Смоленском лютеранском кладбище в Петербурге. Надпись на памятнике на немецком языке гласила: «Здесь покоятся останки знаменитого во всём свете Леонарда Эйлера, мудреца и праведника. Родился в Базеле 4 апреля 1707 года, умер 7 сентября 1783 года»





























