а4)
х ³
(
х ⁶ )
(
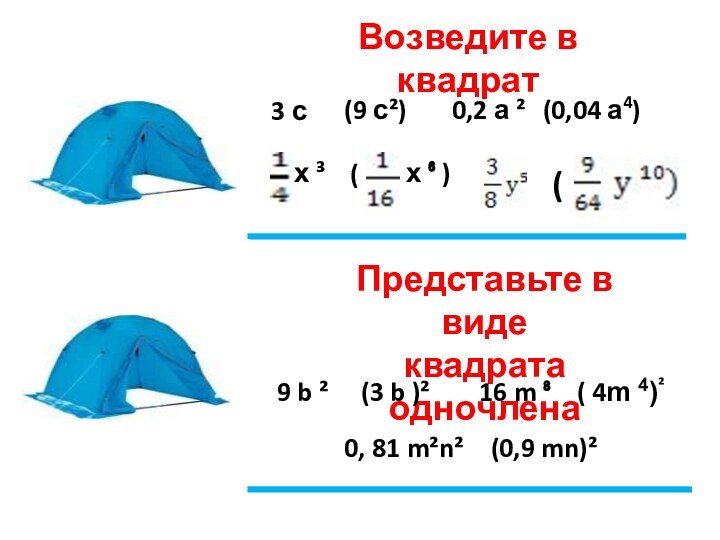
Представьте в виде
квадрата одночлена
9
b ² (3 b )²
16 m ⁸
( 4m 4)²
(0,9 mn)²
0, 81 m²n²
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть









(3 b )²
16 m ⁸
( 4m 4)²
(0,9 mn)²
0, 81 m²n²
(x – 2)²
=X²- 4x + 4
=9 + 6a + a²
(3 + a)²
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа
(a – b)² = a² - 2 ab + b²
(a – b)(a +b) = a² - b²
Произведение разности двух чисел и их суммы равно разности квадратов этих чисел
Представьте в виде многочлена
(2 а + b) (2а – b)
(0,2 у – 4) (0,2у + 4)
(5а - b³) (5a + b³)
Проверьте
x² - 9y²
(0,1x)² - 6² = 0,01x² - 36
(3x²)²- 1² = 9x4 - 1
4a² - b²
0,04y² - 16
(5a)² - (b³)² = 25a² - b²
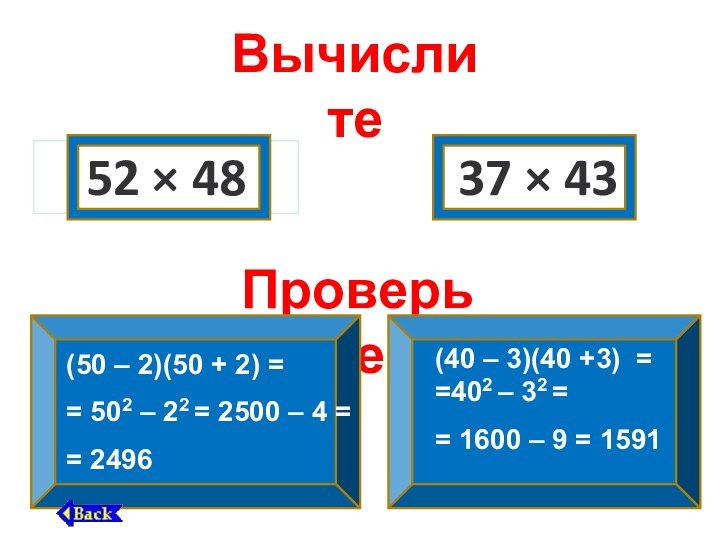
(40 – 3)(40 +3) = =402 – 32 =
= 1600 – 9 = 1591
( 4х² - 3у²) (4х² + 3 у²)
(с³ - 7) (с³ + 7)
Получите имя великого математика
д
м
Е
л
о
н
а
в
ч
г
ф
и
б
к
у
Историческая справка