Презентация на тему Действительные числа и преобразования алгебраических выражений

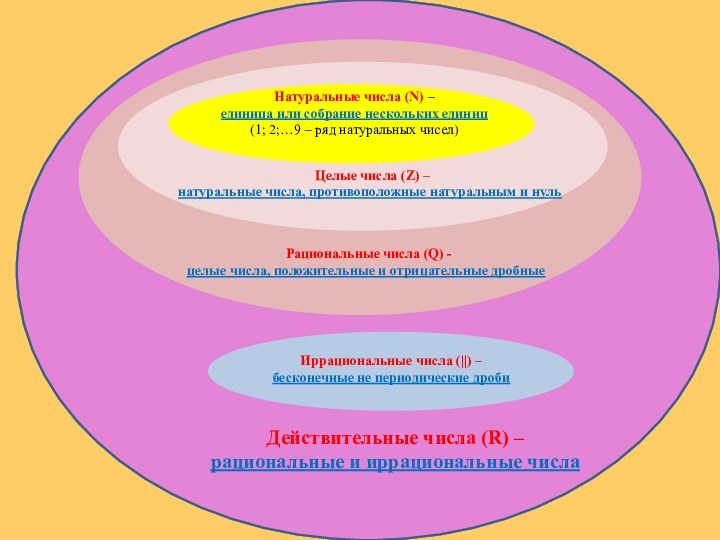
единиц
(1; 2;…9 – ряд натуральных чисел)
Целые числа (Z) –
натуральные

числа, противоположные натуральным и нуль

Рациональные числа (Q) -
целые числа, положительные и отрицательные дробные

Действительные числа (R) –
рациональные и иррациональные числа

Иррациональные числа (||) –
бесконечные не периодические дроби

делятся на себя и на единицу

Четные -
делящиеся на

2 и число 0. (2п)
Нечетные – остальные (2п+1; 2п-1).

Признаки делимости:
На 2 -
На 3 -
На 5 -
На 9 -
На 10 -

Любое составное число можно разложить на простые множители

Задание: разложить на простые множители числа; 1260; 248; 4725
Найти НОК и НОД чисел (54; 72; ) ;(96; 124)(125; 325); (34; 68)

Составные – остальные.

одинаковых долей
единицы называется обыкновенной дробью
Дробь, у которой знаменатель

есть единица с одним или несколькими нулями,
называется десятичной дробью

2/3 = 0,666… – бесконечная периодическая дробь, 0,666…= 0,(6)

0,(68) – чистая периодическая дробь
1, 4(35) – смешанная периодическая дробь

обратить чистую периодическую дробь в обыкновенную, нужно ее период

сделать числителем, а в знаменателе записать цифру 9 столько раз, сколько цифр в периоде.


Чтобы обратить смешанную периодическую дробь в обыкновенную, нужно из числа, стоящего после запятой до второго периода, вычесть число, стоящее после запятой до первого периода, и эту разность сделать числителем, а в знаменатель записать цифру 9 столько раз, сколько цифр в периоде, со столькими нулями справа, сколько цифр между запятой и первым периодом.