- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение тригонометрических функции
Содержание
- 2. ОПРЕДЕЛЕНИЕ Числовые функции, заданные формулами y =sin
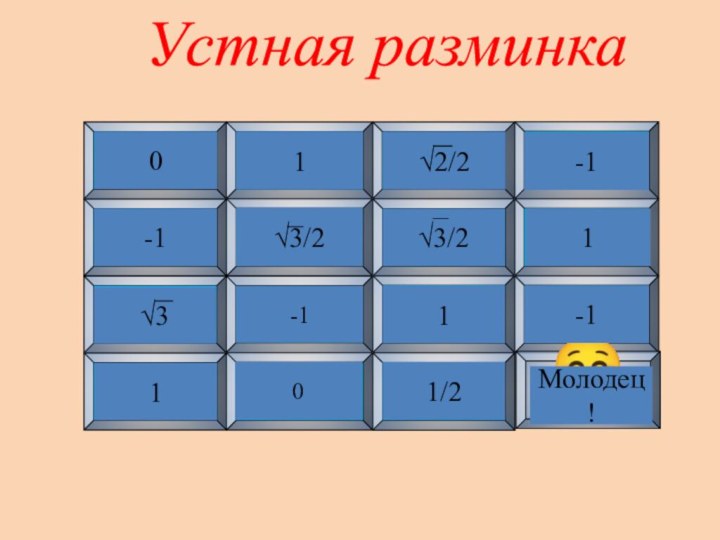
- 3. Устная разминка123456789101112131415☺cos90°sin90°sin(π/4)cos180°sin270°sin(π/3)cos(π/6)cos360°ctg(π/6)tg(π/4)sin(3π/2)cos(2π)cos(-π/2)cos(π/3)cos(‒π)0-111-1011/2-11-1Молодец!
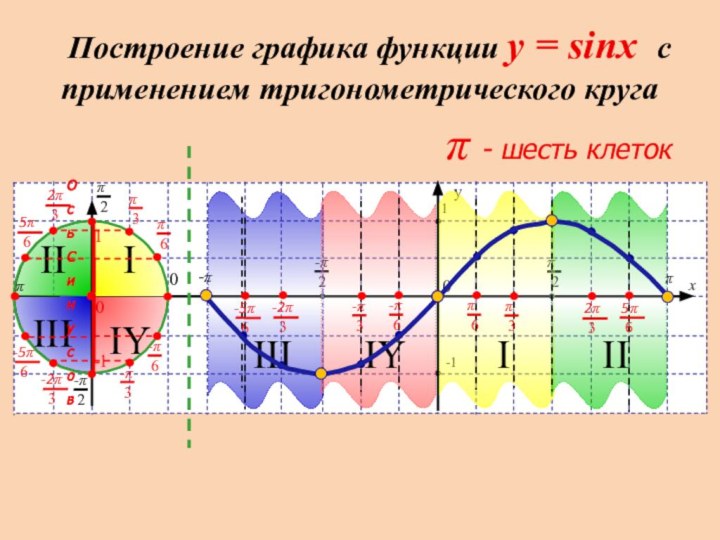
- 4. III IIIIY IIIIYIIIp - шесть клетокОсь Синусов
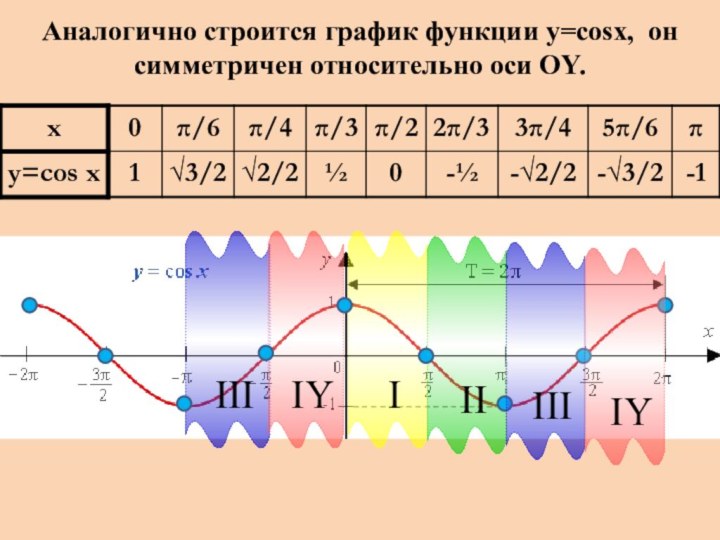
- 5. Аналогично строится график функции y=cosx, он симметричен относительно оси OY.IIIIYIIIIIIIY
- 6. Свойства функции y = cos xОбласть определения:
- 7. Свойства функции y = cos x (продолжение)Функция
- 8. Свойства функции y = sin xОбласть определения:
- 9. Свойства функции y = sin x (продолжение)Функция
- 10. Преобразование графиков тригонометрических функций.Построение графика функции у = sinx + my= sin(x+t)y=f(kx) y=kf(x)
- 11. График
- 12. График
- 13. Если
- 14. Если
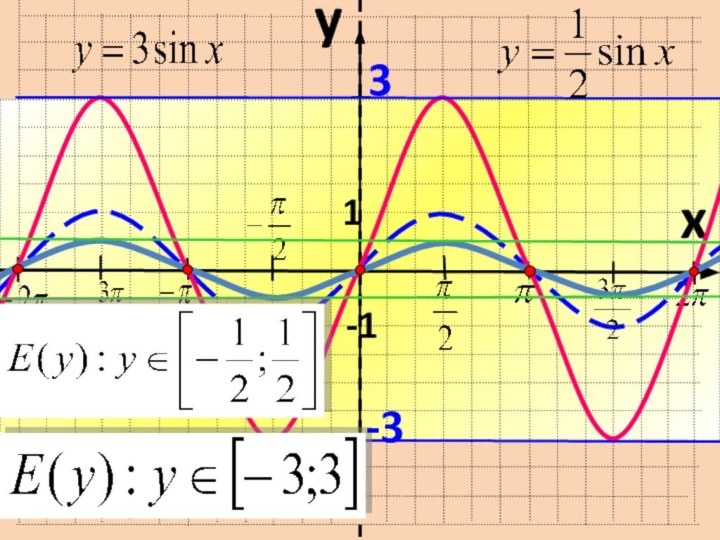
- 15. yx 1-13-3
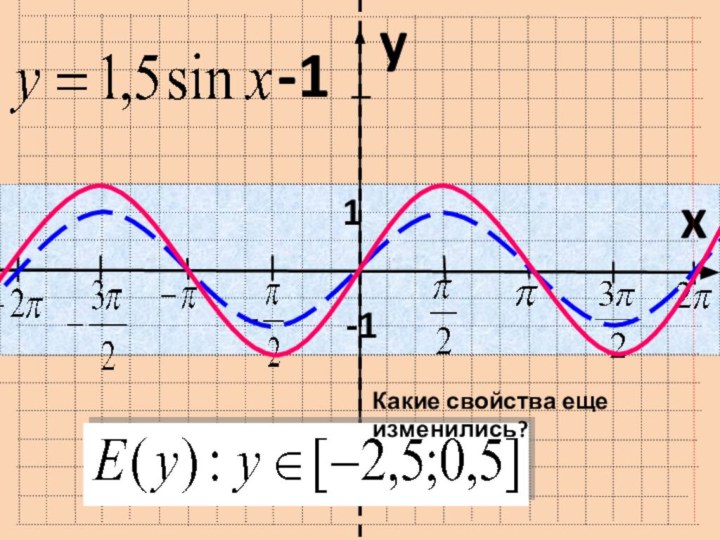
- 17. yx 1-1-1Какие свойства еще изменились?
- 19. Скачать презентацию
- 20. Похожие презентации
ОПРЕДЕЛЕНИЕ Числовые функции, заданные формулами y =sin x и y = cos x, называют соответственно синусом и косинусом.


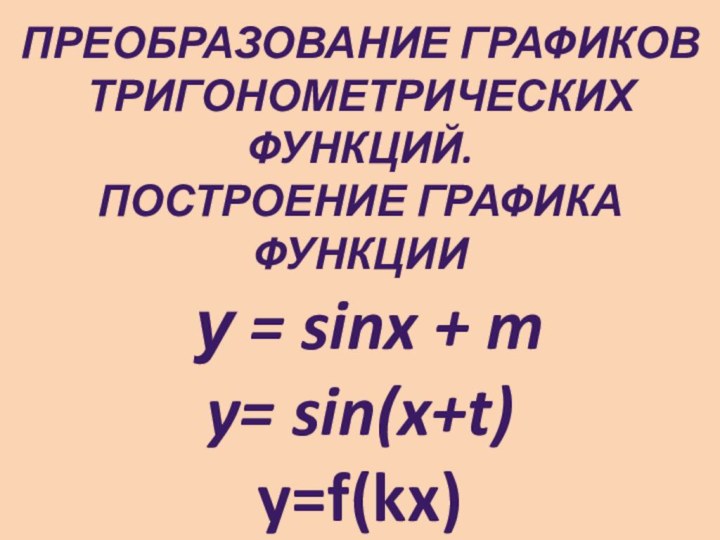

Слайд 3
Устная разминка
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
☺
cos90°
sin90°
sin(π/4)
cos180°
sin270°
sin(π/3)
cos(π/6)
cos360°
ctg(π/6)
tg(π/4)
sin(3π/2)
cos(2π)
cos(-π/2)
cos(π/3)
cos(‒π)
0
-1
1
1
-1
0
1
1/2
-1
1
-1
Молодец!
Слайд 4
III
II
I
IY
III
IY
I
II
p - шесть клеток
О
с
ь
С
и
н
у
с
о
в
Построение
графика функции y = sinx с применением тригонометрического круга
Слайд 6
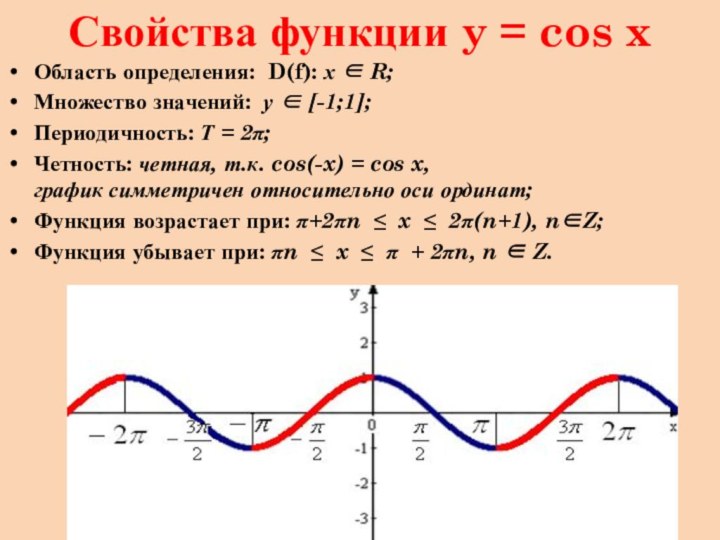
Свойства функции y = cos x
Область определения: D(f):
х R;
Множество значений: у [-1;1];
Периодичность: Т =
2;Четность: четная, т.к. cos(-x) = cos x, график симметричен относительно оси ординат;
Функция возрастает при: +2n x 2(n+1), nZ;
Функция убывает при: n x + 2n, n Z.
Слайд 7
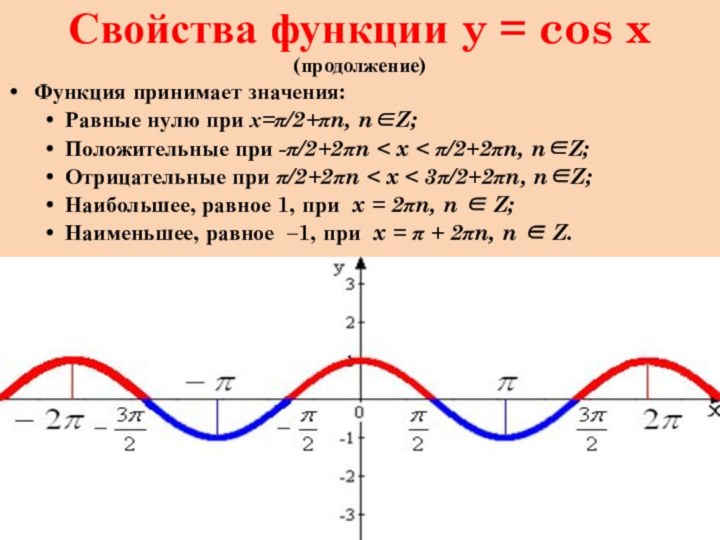
Свойства функции y = cos x (продолжение)
Функция принимает
значения:
Равные нулю при х=/2+n, nZ;
Положительные при -/2+2n x
/2+2n, nZ;Отрицательные при /2+2n x 3/2+2n, nZ;
Наибольшее, равное 1, при x = 2n, n Z;
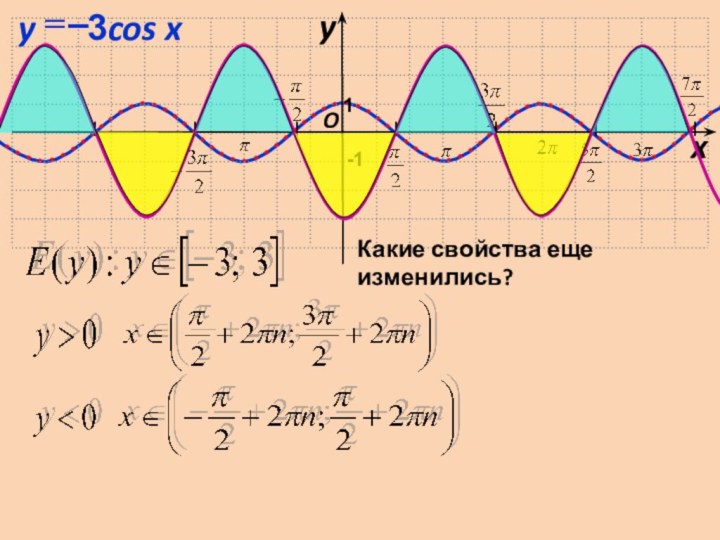
Наименьшее, равное –1, при x = + 2n, n Z.
Слайд 8
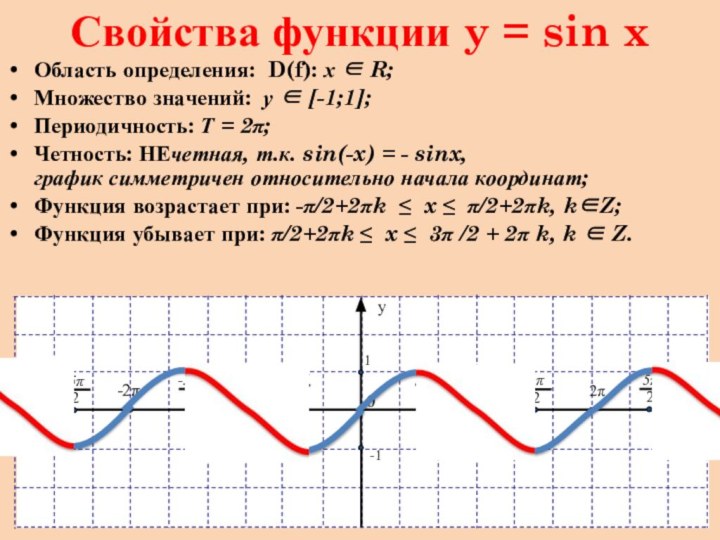
Свойства функции y = sin x
Область определения: D(f):
х R;
Множество значений: у [-1;1];
Периодичность: Т =
2;Четность: НЕчетная, т.к. sin(-x) = - sinx, график симметричен относительно начала координат;
Функция возрастает при: -/2+2k x /2+2k, kZ;
Функция убывает при: /2+2k x 3 /2 + 2 k, k Z.
Слайд 9
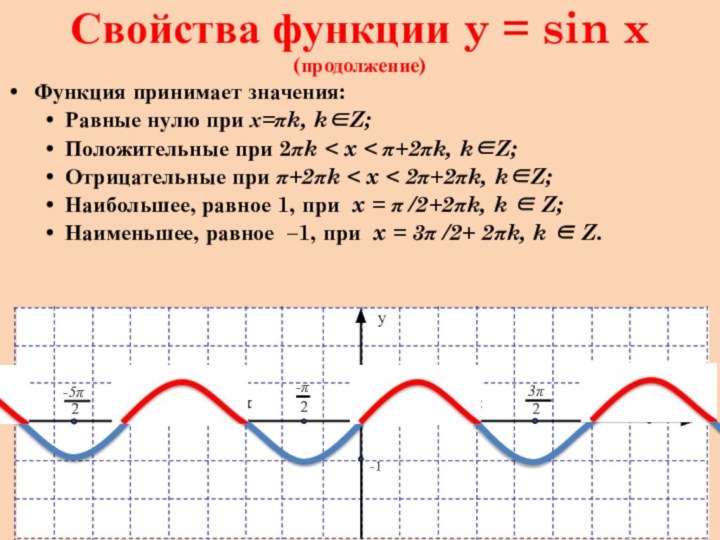
Свойства функции y = sin x (продолжение)
Функция принимает
значения:
Равные нулю при х=k, kZ;
Положительные при 2k x
+2k, kZ;Отрицательные при +2k x 2+2k, kZ;
Наибольшее, равное 1, при x = /2+2k, k Z;
Наименьшее, равное –1, при x = 3 /2+ 2k, k Z.
Слайд 10
Преобразование графиков тригонометрических функций.
Построение графика функции
у =
sinx + m
y= sin(x+t)
y=f(kx)
y=kf(x)
Слайд 11
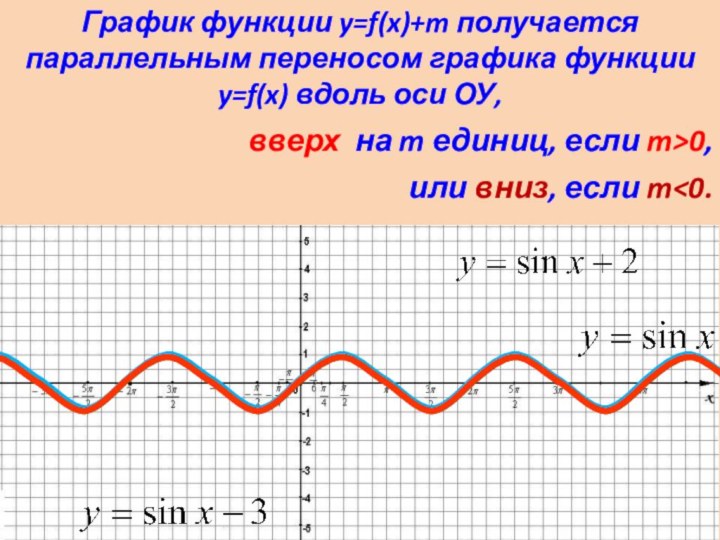
График функции
y=f(x)+m получается параллельным переносом графика функции y=f(x) вдоль оси
ОУ,вверх на m единиц, если m>0,
или вниз, если m<0.
Слайд 12
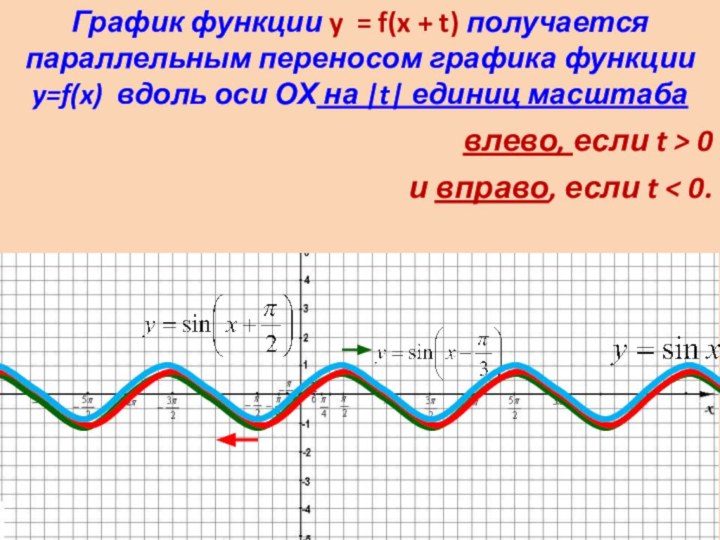
График функции
y = f(x + t) получается параллельным переносом графика
функции y=f(x) вдоль оси ОХ на |t| единиц масштабавлево, если t > 0
и вправо, если t < 0.
Слайд 13
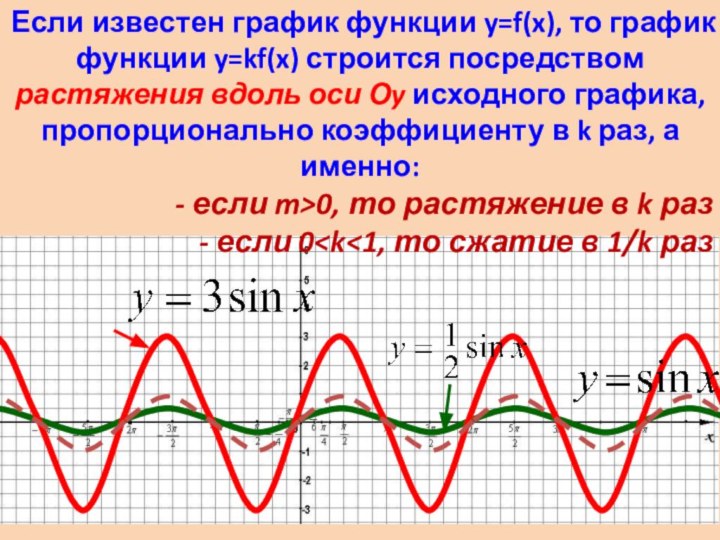
Если известен
график функции y=f(x), то график функции y=kf(x) строится посредством
растяжения вдоль оси Оy исходного графика, пропорционально коэффициенту в k раз, а именно:- если m>0, то растяжение в k раз
- если 0
Слайд 14
Если известен
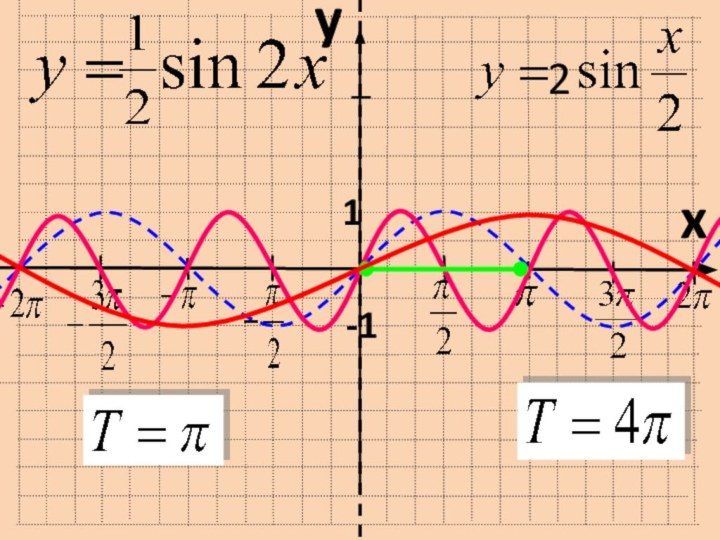
график функции y=f(x), то график функции y=f(kx) строится посредством
сжатия
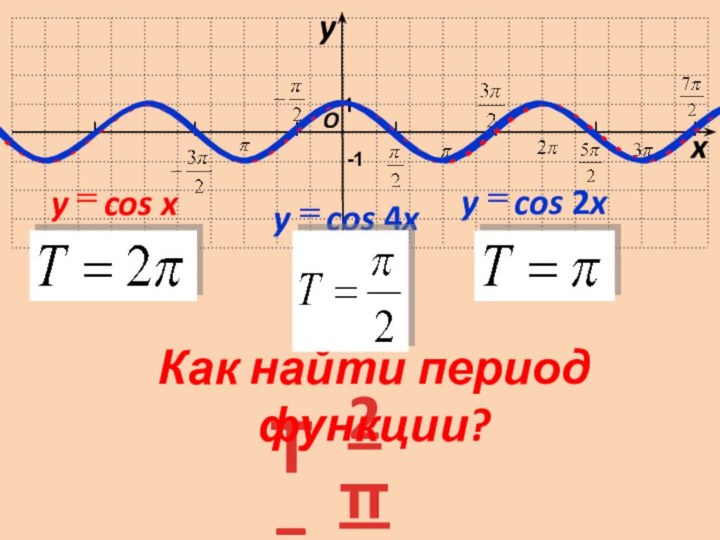
по оси Оx исходного графика пропорционально коэффициенту k при аргументе, а именно: - если k>1, то сжатие в k раз
- если 0