- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сумма углов треугольника
Содержание
- 2. Рассмотрим произвольный треугольник АВС АВС
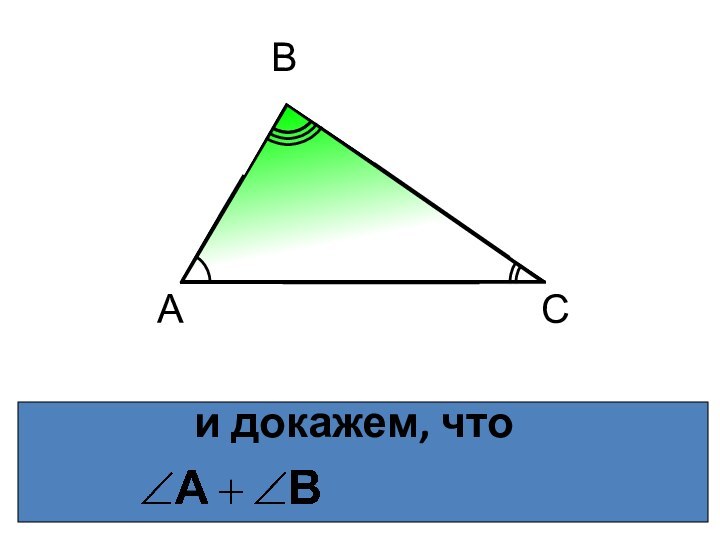
- 3. и докажем, что АВС
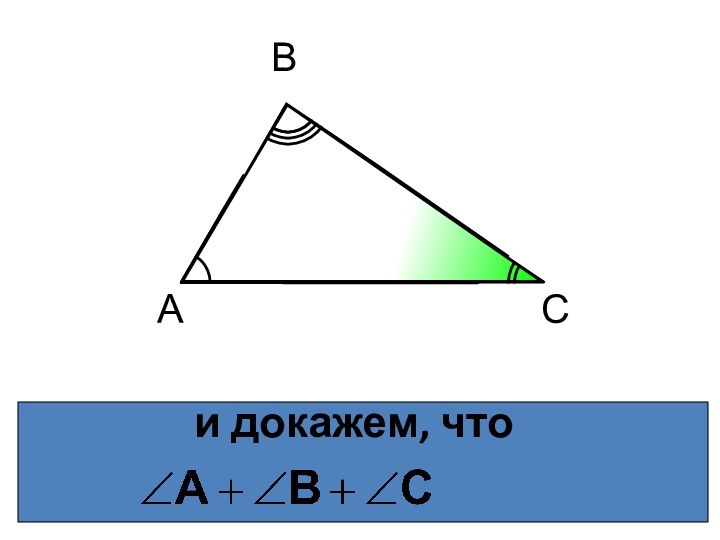
- 4. и докажем, что АВС
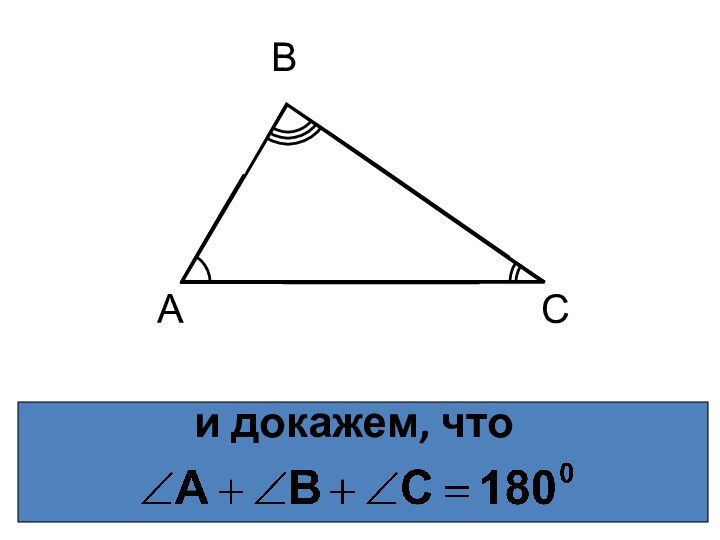
- 5. и докажем, что АВС
- 6. и докажем, что АВС
- 7. Проведем через вершину В прямую , параллельную стороне АС АСВС
- 8. Углы 1 и 4 являются накрест лежащими
- 9. А углы 3 и 5 являются накрест
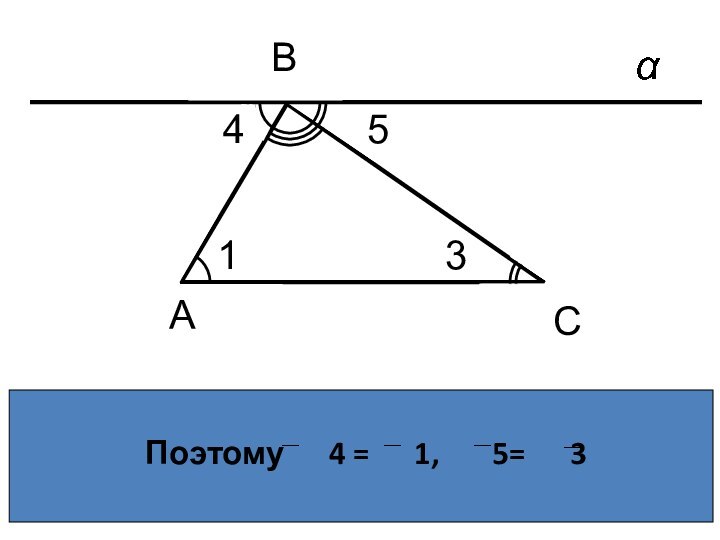
- 10. Поэтому 4 = 1, 5= 3 АС3В541С
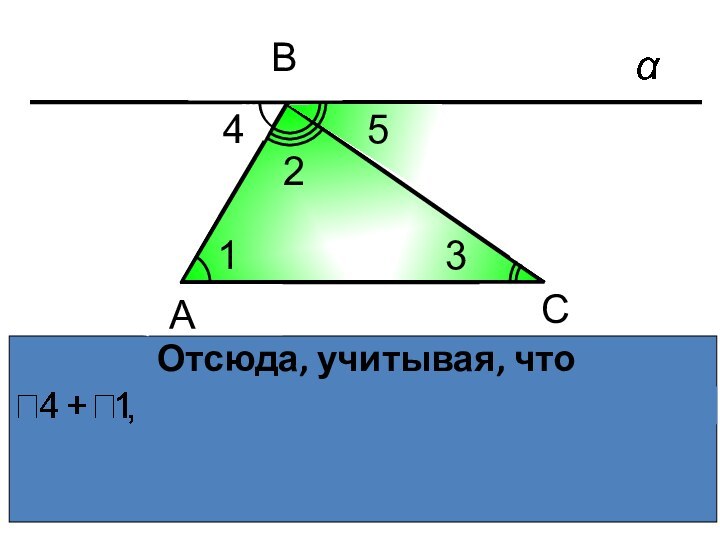
- 11. Очевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т.е. АС2СВ45
- 12. Отсюда, учитывая, что получаем илиА2С513В4
- 13. Отсюда, учитывая, что получаем илиА2СВ1354
- 14. Теорема доказана
- 15. Скачать презентацию
- 16. Похожие презентации
Рассмотрим произвольный треугольник АВС АВС








Слайд 8
Углы 1 и 4 являются накрест лежащими углами
при пересечении параллельных прямых и АС
и секущей АВ.А
С
В
1
4
С
Слайд 9
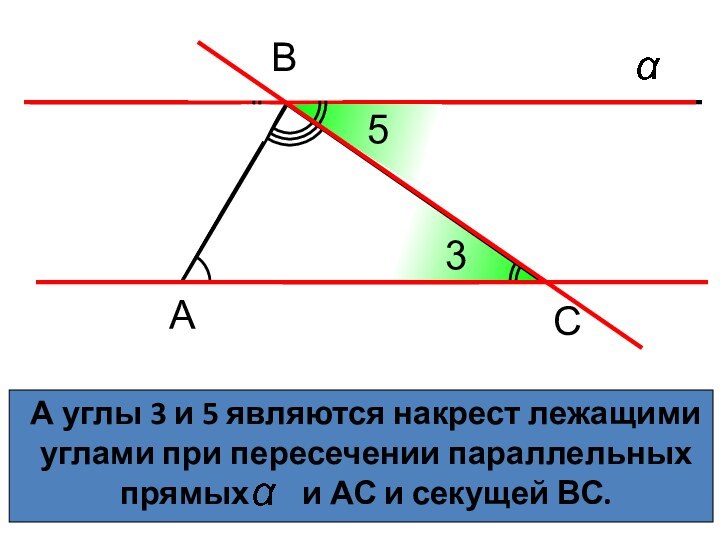
А углы 3 и 5 являются накрест лежащими
углами при пересечении параллельных прямых и
АС и секущей ВС.А
С
В
С
5
3





























