Презентация на тему к уроку Независимые события

из них меняется в зависимости от того, произойдет другое

событие или нет.

них не изменяет вероятность появления другого.
Например: опыт состоит в

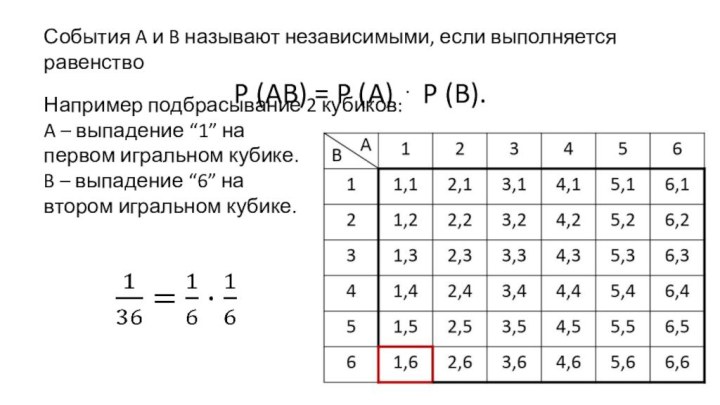
бросании двух монет. Пусть А и В – события, состоящие в том, что орёл появится соответственно на первой и второй монете. В данном случае вероятность события А не зависит от того, произошло событие В или нет. Следовательно, событие А независимо от события В.

равенство
P (AB) = P (A) ⋅ P (B).
Например подбрасывание

2 кубиков:
A – выпадение “1” на
первом игральном кубике.
B – выпадение “6” на
втором игральном кубике.

десяти натуральных чисел и рассматриваются события:
A – названо чётное

число, B – названо число, кратное пяти.
Выяснить являются ли события A и B независимыми.

от друга видеокамеры . Вероятность того , что течение

суток первая видеокамера выйдет из строя равна 0,001 , а вероятность того , что выйдет из строя вторая , равна 0,0005 . Найти вероятность , что в течение суток выйдут из строя обе видеокамеры.