Презентация на тему Формула решения квадратных уравнений

по теме «Решение квадратных уравнений»с целью повторения и обобщения

изученного материала
Отдельные части работы могут быть использованы и на обучающих уроках или во внеклассной работе с целью ознакомления с дополнительными сведениями.

(тест)
Кроссворд
Это интересно (дополнительные сведения о решении квадратных уравнений)
Из истории

решения квадратных уравнений
Проверь себя (решение квадратного уравнения при помощи языка программирования)
Использованная литература

уравнения по формуле

где х – переменная, а,в,с – некоторые числа, причем

а≠0.
Числа а, в, с – коэффициенты квадратного уравнения. Число а – первый коэффициент, в – второй коэффициент, с – свободный член.
Если в квадратном уравнении ах²+вх+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется неполным квадратным уравнением.
Квадратное уравнение, в котором коэффициент а=1 называется приведенным квадратным уравнением.

с=1,2;
б) 5х²-2=0 – неполное квадратное уравнение, где

а=5, в=0, с=-2;
в) -3х²+7х=0 - неполное квадратное уравнение, где а=-3, в=7, с=0;
г) 7х²=0 - неполное квадратное уравнение, где а=7, в=0, с=0;
д) х²+4х-12=0 – приведенное квадратное уравнение, где а=1, в=4, с=-12.

дискриминант
D=в²-4ас
Если D=0, то

2 корня
Если D>0, то

1 корень
Уравнение не
имеет

корней

а=3; в=11;с=6.
D=11²-4*3*6=121-72=49>0 – уравнение имеет 2 корня

– уравнение имеет 1 корень.

Х=

в=3;с=-5.
D=3²-4*(-2)*5=9-40=-31

Установить верный ответ из числа предложенных.

:
Ответы давать : да или нет. Время для выполнения

– 10 минут.
Указание: не выполнять задания 8 и 9.
Текст теста:

для выполнения – 15 минут.
Указание: не выполнять задания 6

и 7.
Текст теста:

коэффициент равен 1.
3. Уравнения с одной переменной, имеющие одни

и те же корни.
4. Числа а,в и с в квадратном уравнении.
5. Значение переменной, при котором уравнение обращается в верное равенство.
6. Равенство, содержащее неизвестное.
7. Неотрицательное значение квадратного корня.
8. Древнегреческий математик, который нашел приемы решения квадратных уравнений без обращения к геометрии.
9. Квадратное уравнение, в котором хотя бы один из коэффициентов в или с равен 0.
10. «Дискриминант» - по-латыни.
11. Коэффициент с квадратного уравнения.
12. Французский математик, который вывел формулы, выражающие зависимость корней уравнения от его коэффициентов.

Если вы разгадаете этот кроссворд верно, то сможете в выделенном вертикальном столбце прочитать термин, относящийся к теме.

уравнения в особых случаях):
1 случай. Если a+b+c=0, то х1=1;

х2= с/а
2 случай. Если a-b+c=0, то х1=-1; х2= -с/а
Нахождение корней приведенного квадратного уравнения: х²+px+q=0. здесь полезно воспользоваться формулой:


Формула запоминается надолго, если выучить ее в стихотворной форме:

обратным,
На два мы его разделим.
И от корня аккуратно
Знаком минут-плюс

отделим.
А под корнем, очень кстати,
Половина «пэ» в квадрате,
Минус «ку». И вот решенье
Небольшого уравненья.

решать еще в Древнем Вавилоне во II тысячелетии до

н.э. Математики Древней Греции решали квадратные уравнения геометрически; например, ЕвклидУравнения 2-ой степени умели решать еще в Древнем Вавилоне во II тысячелетии до н.э. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид – при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактатах. Например.

первых дошедших до наших дней выводов этой формулы принадлежит

индийскому математику Брахмагупте (около 598 г.).
Среднеазиатский ученый ал-ХорезмиСреднеазиатский ученый ал-Хорезми (IX в.) в трактате «Китаб аль-джебр валь -мукабала» получил эту формулу методом выделения полного квадрата с помощью геометрической интерпретации. См.подробнее.

Из истории решения квадратных уравнений.

видна из рисунка (рассматривается решение уравнения х²+10х=39. Площадь большого

квадрата равна (х+5)². Она складывается из площади х²+10х фигуры, закрашенной голубым цветом, равной левой части рассматриваемого уравнения, и площади четырех квадратов со стороной 5/2, равной 25. Таким образом, (х+5)²=39+25; х1=3; х2=-13.

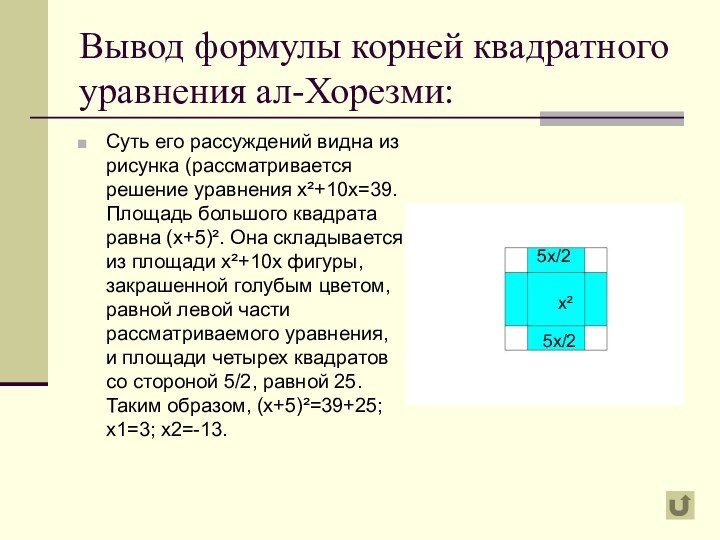
х²

5х/2

5х/2

II в.до н.э.)
«Имеется город с границей в виде квадрата

со стороной неизвестного размера, в центре каждой стороны находятся ворота. На расстоянии 20 бу(1 бу=1,6 м) от северных ворот (вне города) стоит столб. Если пройти от южных ворот прямо 14 бу, затем повернуть на запад и пройти еще 1775 бу, то можно увидеть столб. Спрашивается: какова сторона границы города?»
Решение смотри здесь:

х. Из подобия треугольников BED и ABC (см.рис.) получим:

k/0.5x=(k+x+l)/d.
Поэтому, чтобы определить неизвестную сторону квадрата, получаем квадратное уравнение х2+(k+l)-2kd=0.
В данном случае уравнение имеет вид х2+34х-71000=0, откуда х=25000 бу.
Отрицательных корней (в данном случае х=-284) китайские математики не рассматривали, хотя в этом же трактате содержатся операции с отрицательными числами.

l

программирования):
Программа, позволяющая решать квадратные уравнения (язык Turbo Pascal)

2002 год
Макарычев Ю.Н. Алгебра, 8 класс – Москва, «Просвещение»,

2000 год
Ткачева М.В. Домашняя математика, 8 класс- Москва, «Просвещение», 1996 год
Худадатова С.С. Математика в ребусах, кроссвордах – Москва, «Школьная Пресса», 2003 год
Энциклопедический словарь юного математика –Москва, «Педагогика», 1985 год
Энциклопедия «Я познаю мир. Математика» - Москва, АСТ, 1996 год.

«Усовершенствованное учение Брахмы» («Брахмаспхутасиддханта», 628 г.), значительная часть которого

посвящена арифметике и алгебре. Брахмагупта , изложил общее правило решения квадратных уравнений, приведенных к единой канонической
форме:
ax2 + bх = с, а> 0. (1)
В уравнении (1) коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

труде «Арифметика» (сохранились 6 книг из 13), дал решение

задач, приводящихся к т.н. диофантовым уравнениям, и впервые ввел буквенную символику в алгебру.

Лавный труд «Начала»(15 книг), содержит основы античной математики, элементарной

геометрии, теории чисел, общей теории отношений и метода определения площадей и объемов, включавшего элементы теории пределов, оказал огромное влияние на развитие математики.

ибн Муса аль-Хорезми (то есть, родом из Хорезма -

с берегов Сыр-Дарьи). Он работал в первой половине 9 века и был любимцем ученейшего из халифов - Маамуна (сына знаменитого Гаруна ар-Рашида). Главная книга Хорезми названа скромно: "Учение о переносах и сокращениях", то есть техника решения алгебраических уравнений. По-арабски это звучит "Ильм аль-джебр ва"ль-мукабала"; отсюда произошло наше слово "алгебра".
Другое известное слово - "алгоритм", то есть четкое правило решения задач определенного типа - произошло от прозвания "аль-Хорезми". Третий известный термин, введенный в математику знаменитым согдийцем - это "синус", хотя в этом деле не обошлось без курьеза.
В алгебраическом трактате ал-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
«Квадраты равны корням», т. е. ах2 = bх.
«Квадраты равны числу», т. е. ах2 = с.
«Корни равны числу», т. е. ах = с.
«Квадраты и числа равны корням», т. е. ах2 + с = bх.
«Квадраты и корни равны числу», т. е. ах2 + bх =с.
«Корни и числа равны квадратам», т. е. bх + с == ах2.
Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно,не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Уравнение.
7. Арифметический.
8. Диофант.
9. Неполное.
10. Различитель.
11. Свободный.
12. Виет.
В выделенном столбце

: ДИСКРИМИНАНТ

нет.
Вариант 2. 1,3,4,10 – да; 2,5,6,7 - нет