- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Готовимся к ОГЭ - 11 (2 часть. Геометрические задачи на вычисление)
Содержание
- 2. СодержаниеРешение задач по теме «Углы» Решение задач по теме «Треугольники» Дидактический материалДидактический материал
- 3. Решение задач по теме «Углы»
- 4. Задача 1Найдите угол АСО, если его сторона СА касается окружности, О —
- 5. РешениеПроведём радиус OA. Треугольник AOC — прямоугольный, ∠OAC = 90°. ∠COA = 180° − ∠AOD = =180° − 100°= 80°; ∠ACO = 90° − 80° = 10°.Ответ: 10.СD
- 6. О25°Задача 2Найдите величину угла АОЕ , если ОЕ — биссектриса угла АОС , ОD — биссектриса угла СОВ.АECDB
- 7. РешениеИмеем: /_СОВ = 2 · 25° =50°; /_АОС = 180°
- 8. Задача 3На сторонах угла ВАС и на его биссектрисе
- 9. РешениеТреугольники ADB и ACD равнобедренные и равны по двум
- 10. Задача 4В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.АBC40°60°HD?
- 11. РешениеИз ∆АВС найдем /_АВС : /_АВС =
- 12. Задача 6В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.АВСНD
- 13. РешениеИз треугольника АВС найдем /_АВС = 180°
- 14. Задача 5BACK
- 15. Решение
- 16. Дидактический материал
- 17. К ЗАДАЧЕ №1№1. Найдите угол АСО, если его
- 18. К ЗАДАЧЕ №21). Найдите величину угла АОЕ,
- 19. К ЗАДАЧЕ №31). На сторонах угла ВАС и на
- 20. К ЗАДАЧЕ №41). В треугольнике АВС углы А и С равны 20° и
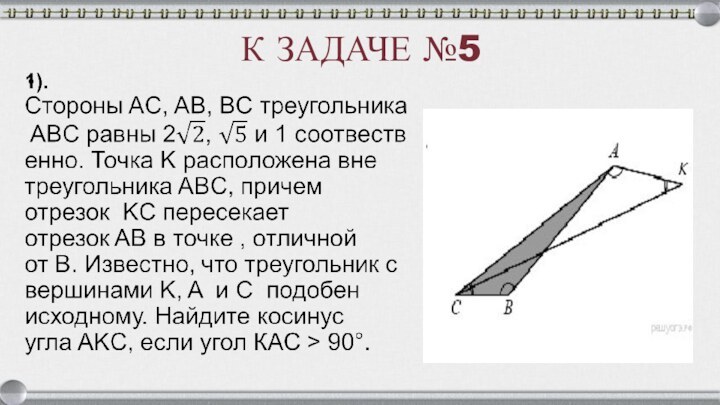
- 21. К ЗАДАЧЕ №5
- 22. К ЗАДАЧЕ №61). В треугольнике АВС углы А и С равны 40° и
- 23. Решение задач по теме «Треугольники»
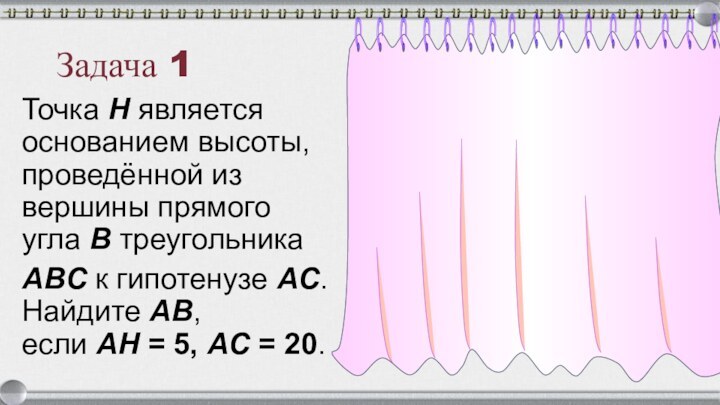
- 24. Задача 1 Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 5, AC = 20.
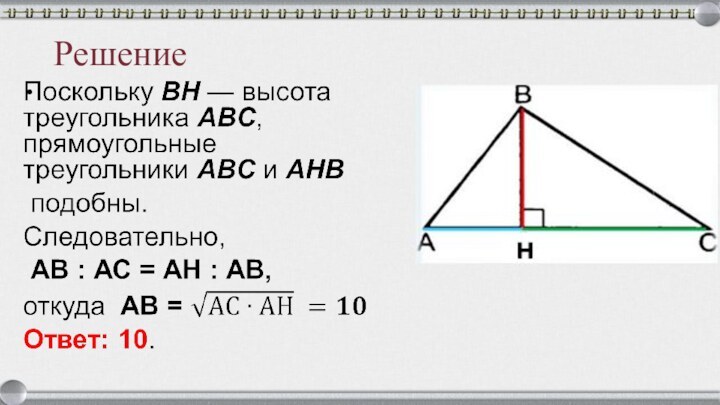
- 25. Решение
- 26. Задача 2 Точка H является основанием высоты BH, проведённой из
- 27. РешениеУгол АВС — вписанный, он равен 90° и опирается
- 28. Задача 3 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 16, DC = 24, AC = 25 .AВСDM
- 29. Решение
- 30. Задача 4 Окружность пересекает стороны AB и AC ∆ABC в точках K и P соответственно и
- 31. Решение
- 32. Продолжение
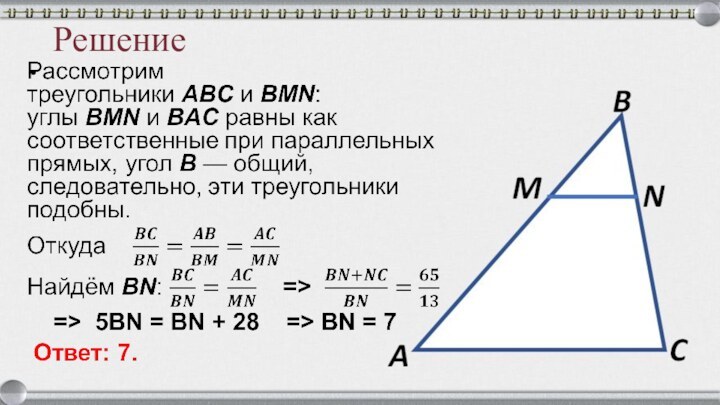
- 33. Задача 5 Прямая, параллельная стороне AC ∆ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 13, AC = 65, NC = 28.ABCMN
- 34. Решение
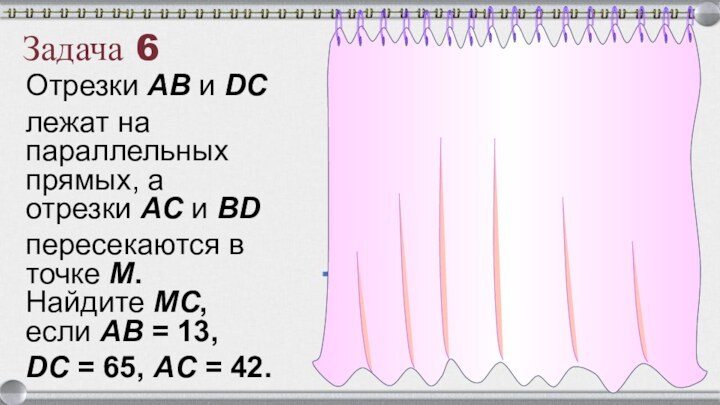
- 35. Задача 6 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 13, DC = 65, AC = 42.
- 36. Решение
- 37. Задача 7 Точка H является основанием высоты BH, проведённой из
- 38. РешениеУгол PBK — вписанный, он равен 90° и опирается
- 39. Дидактический материал
- 40. К задаче № 11). Точка H является основанием высоты,
- 41. К задаче № 21). Точка H является основанием высоты BH,
- 42. К задаче № 31). Отрезки AB и DC лежат на параллельных
- 43. К задаче № 41). Окружность пересекает стороны AB и AC треугольника ABC в
- 44. Скачать презентацию
- 45. Похожие презентации
СодержаниеРешение задач по теме «Углы» Решение задач по теме «Треугольники» Дидактический материалДидактический материал



























Слайд 4
Задача 1
Найдите угол АСО, если его сторона СА касается окружности, О — центр
окружности, а дуга AD окружности, заключённая внутри этого угла, равна 100°.
Проведём радиус OA. Треугольник AOC — прямоугольный, ∠OAC = 90°. ∠COA = 180° − ∠AOD = 180° − 100° = 80 Проведём радиус OA. Треугольник AOC — прямоугольный, ∠OAC = 90°. ∠COA = 180° − ∠AOD = 180° − 100° = 80
С
D
Слайд 5
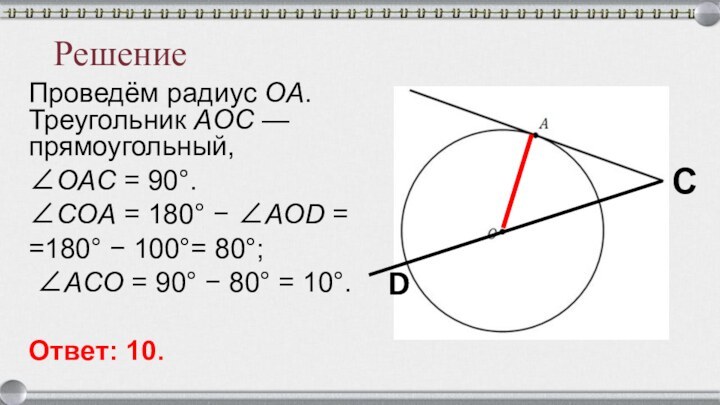
Решение
Проведём радиус OA. Треугольник AOC — прямоугольный,
∠OAC = 90°.
∠COA = 180° − ∠AOD =
=180° − 100°= 80°;
∠ACO = 90° − 80° = 10°.
Ответ: 10.
С
D
Слайд 6
О
25°
Задача 2
Найдите величину угла АОЕ , если ОЕ — биссектриса
угла АОС , ОD — биссектриса угла СОВ.
А
E
C
D
B
Слайд 7
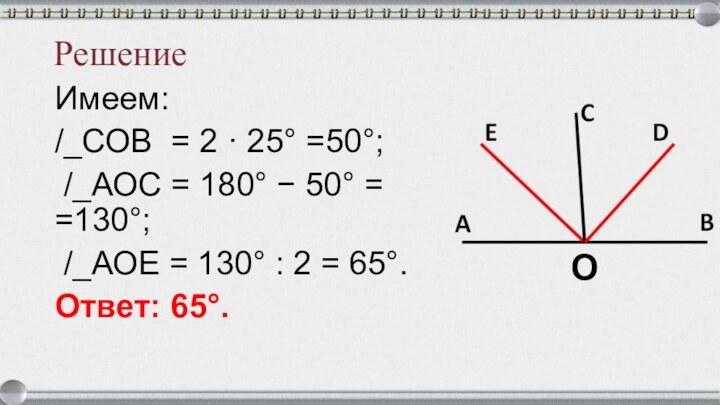
Решение
Имеем:
/_СОВ = 2 · 25° =50°;
/_АОС = 180° −
50° = =130°;
/_АОЕ = 130° : 2 =
65°.Ответ: 65°.
О
Слайд 8
Задача 3
На сторонах угла ВАС и на его биссектрисе отложены
равные отрезки АВ; АС и АD. Величина угла ВDС равна 160°. Определите
величину угла ВАС.А
B
C
D
Слайд 9
Решение
Треугольники ADB и ACD равнобедренные и равны по двум сторонам
и углу между ними.
Следовательно,
/_ACD = /_CDA = /_ADB
= = 80°
/_BAC = 360° − 4 · 80° = 40°.
Ответ: 40°.
Слайд 10
Задача 4
В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите
угол между высотой ВН и биссектрисой BD.
А
B
C
40°
60°
H
D
?
Слайд 11
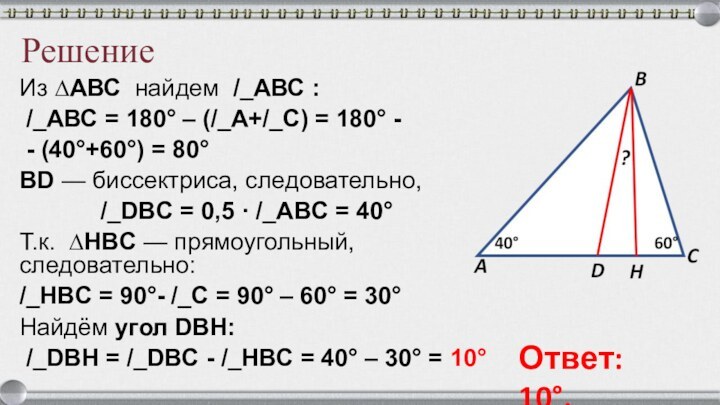
Решение
Из ∆АВС найдем /_АВС :
/_АВС =
180° – (/_А+/_С) = 180° -
- (40°+60°) =
80°ВD — биссектриса, следовательно,
/_DBC = 0,5 · /_ABC = 40°
Т.к. ∆HBC — прямоугольный, следовательно:
/_HBC = 90°- /_C = 90° – 60° = 30°
Найдём угол DBH:
/_DBH = /_DBC - /_HBC = 40° – 30° = 10°
Ответ: 10°.
Слайд 12
Задача 6
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите
угол между высотой ВН и биссектрисой BD.
А
В
С
Н
D
Слайд 13
Решение
Из треугольника АВС найдем /_АВС = 180° –
(/_А+ /_С) =180° - (20°+60°) = 100°
ВD — биссектриса, следовательно,
/_DBC = 0,5 ·/_ABC = 50°Треугольник HBC — прямоугольный, следовательно:
/_HBC = 90° - /_C = 90° – 60° = 30°
Найдём угол DBH
/_DBH = /_DBC - /_HBC = 50° – 30° = 20°
Ответ: 20°.
Слайд 17
К ЗАДАЧЕ №1
№1. Найдите угол АСО, если его сторона СА касается
окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла,
равна 110°.№2. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 100°
№3. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140° .
Слайд 18
К ЗАДАЧЕ №2
1). Найдите величину угла АОЕ, если
ОЕ — биссектриса угла АОС , ОD — биссектриса угла СОВ.
2). Найдите
величину угла СОЕ , если ОЕ — биссектриса угла АОС, АD — биссектриса угла СОВ.
Слайд 19
К ЗАДАЧЕ №3
1). На сторонах угла ВАС и на его
биссектрисе отложены равные отрезки АВ, АС и АD . Величина угла ВDC равна 160°.
Определите величину угла BAC .2). На сторонах угла BAC, равного 20°, и на его биссектрисе отложены равные отрезки AB, AC и AD. Определите величину угла BDC.
Слайд 20
К ЗАДАЧЕ №4
1). В треугольнике АВС углы А и С равны 20° и 60°
соответственно. Найдите угол между высотой ВН и биссектрисой BD.
2). В треугольнике АВС углы А и С равны 20°
и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.3). В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Слайд 22
К ЗАДАЧЕ №6
1). В треугольнике АВС углы А и С равны 40° и 60°
соответственно. Найдите угол между высотой ВН и биссектрисой BD.
2). В треугольнике АВС углы А и С равны 20°
и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.3). В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Слайд 24
Задача 1
Точка H является основанием высоты, проведённой из вершины
прямого угла B треугольника
ABC к гипотенузе AC. Найдите AB, если AH = 5, AC = 20.
Слайд 26
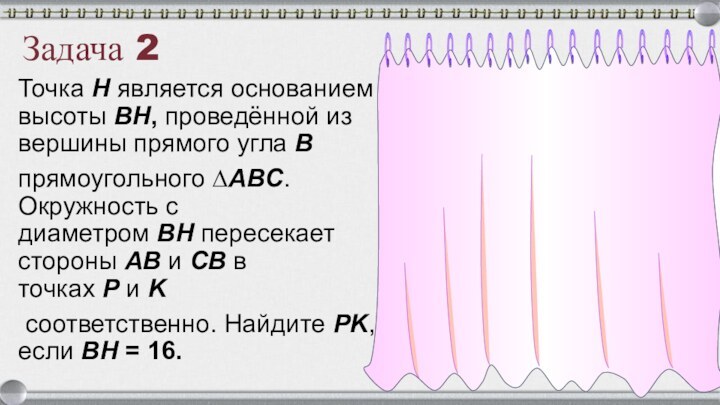
Задача 2
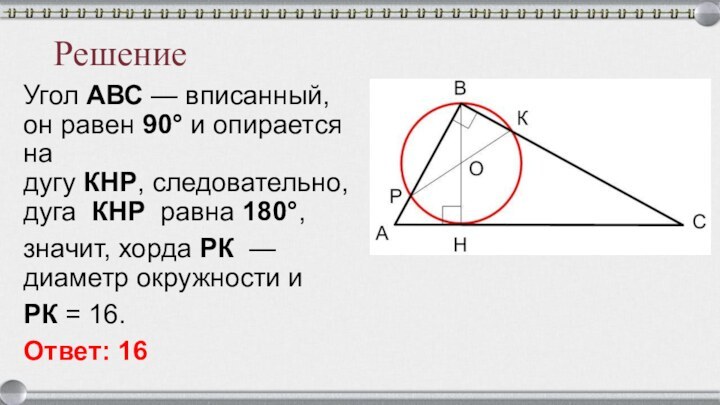
Точка H является основанием высоты BH, проведённой из вершины
прямого угла B
прямоугольного ∆ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K
соответственно. Найдите PK,
если BH = 16.
Слайд 27
Решение
Угол АВС — вписанный, он равен 90° и опирается на
дугу КНР, следовательно, дуга КНР равна 180°,
значит, хорда РК — диаметр
окружности и РК = 16.
Ответ: 16
Слайд 28
Задача 3
Отрезки AB и DC
лежат на параллельных прямых,
а отрезки AC и BD
пересекаются
в точке M. Найдите MC, если AB = 16,
DC = 24, AC = 25 .
A
В
С
D
M
Слайд 30
Задача 4
Окружность пересекает стороны AB и AC
∆ABC в точках K и P соответственно и проходит
через вершины B и C. Найдите длину отрезка KP, если AP = 18, а сторона BC
в 1,2
раза меньше стороны AB.A
B
C
K
P
?
Слайд 33
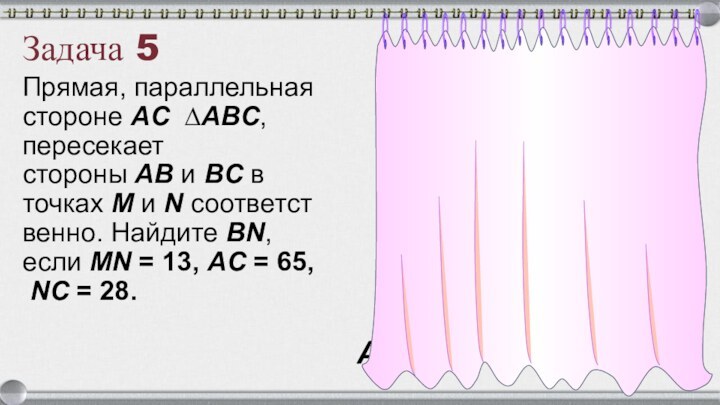
Задача 5
Прямая, параллельная стороне AC ∆ABC, пересекает стороны AB и BC в
точках M и N соответственно. Найдите BN, если MN = 13, AC = 65, NC = 28.
A
B
C
M
N
Слайд 35
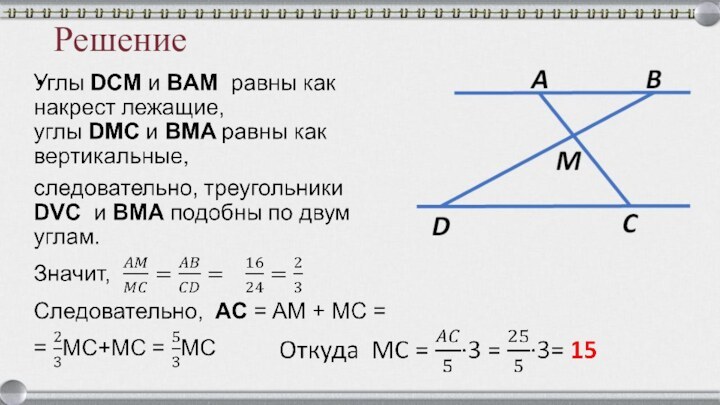
Задача 6
Отрезки AB и DC
лежат на параллельных прямых, а отрезки AC и BD
пересекаются
в точке M. Найдите MC, если AB = 13,
DC = 65, AC = 42.
Слайд 37
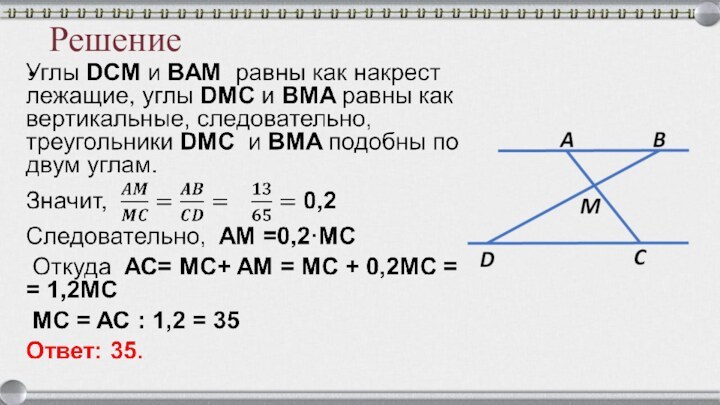
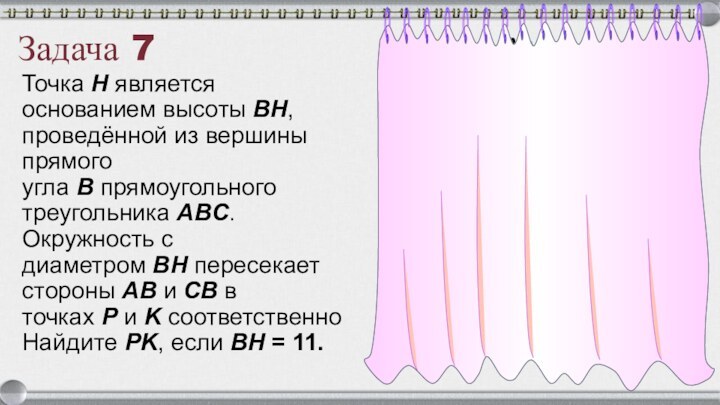
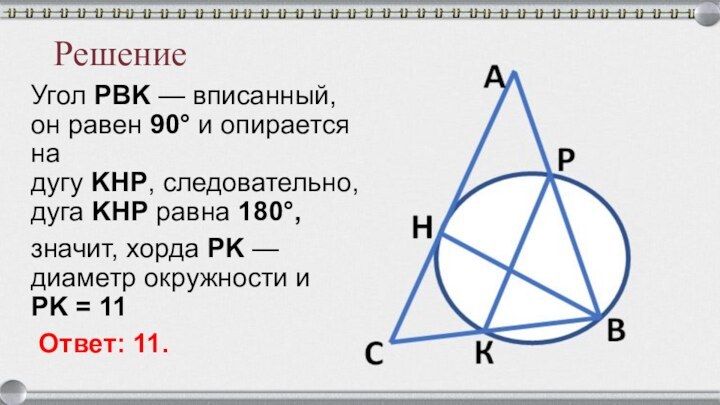
Задача 7
Точка H является основанием высоты BH, проведённой из вершины
прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно Найдите PK,
если BH = 11.A
В
С
Р
К
Н
Слайд 38
Решение
Угол PBK — вписанный, он равен 90° и опирается на
дугу KHP, следовательно, дуга KHP равна 180°,
значит, хорда PK — диаметр окружности и PK
= 11Ответ: 11.
Слайд 40
К задаче № 1
1). Точка H является основанием высоты, проведённой
из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 10, AC = 40.
(20)2). Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 9, AC = 36. (18)
3). Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 5, AC = 45. (15)
Слайд 41
К задаче № 2
1). Точка H является основанием высоты BH, проведённой
из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в
точках P и K соответственно. Найдите PK, если BH = 11. (11)2). Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK = 14. (14)
Слайд 42
К задаче № 3
1). Отрезки AB и DC лежат на параллельных прямых,
а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 12, DC = 48, AC = 35. (28)
2). Отрезки AB и DC лежат
на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 15, DC = 30, AC = 39. (26)3). Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 14, DC = 42, AC=52. (39)
Слайд 43
К задаче № 4
1). Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно
и проходит через вершины B и C. Найдите длину отрезка KP, если AP = 16,
а сторона BC в 1,6 раза меньше стороны AB. (10)2). Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP = 34, а сторона BC в 2 раза меньше стороны AB. (17)