- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Исследовательский проект Решение квадратных уравнений
Содержание
- 2. «Урaвнение - этo зoлoтoй ключ, открывaющий всe
- 3. Цель работы: разработать методическое пособие для учащихся, содержащее
- 4. Гипотеза: любое квадратное уравнение можно решить всеми
- 5. Впервые я услышала о квадратных уравнениях на
- 6. Определение квадратного уравнения, его виды: Квадратным
- 7. Немного из истории:Квадратные уравнения - это фундамент,
- 8. Разложение левой части уравнения на множители:Пример:
- 9. Метод выделения полного квадрата (классический метод).
- 10. Решение квадратных уравнений по формуле с четным коэффициентом.
- 11. Пример:
- 12. Теорема Виета. Б) x2 + 4x
- 13. Решение уравнений способом «переброски»квадратное уравнение ах2 +
- 14. Свойства коэффициентов квадратного уравнения.ах2 + bх +
- 15. Решение квадратных уравнений через дискриминант.
- 16. Пример:
- 17. Выделение полного квадрата двучлена ,если,если,если,если
- 18. Пример:
- 19. Графическое решение квадратного уравнения.х2 + px +
- 20. Пример:Решим графически уравнение х2 - 3х -
- 21. Решим графически уравнение х2 - 2х +
- 22. Решим графически уравнение х2 - 2х +
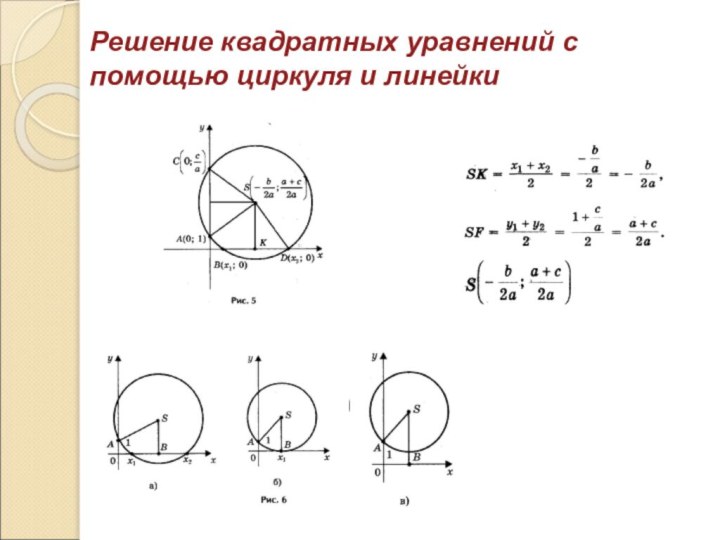
- 23. Решение квадратных уравнений с помощью циркуля и линейки
- 24. Решение квадратных уравнений с помощью номограммы.1)Для уравнения
- 25. Геометрический способ решения квадратных уравненийх2 + 10х
- 26. Заключение:Уравнения – язык алгебры, квадратные уравнения –
- 27. Я составила буклет-памятку, в него вошли те
- 28. Литература:1. Алимов Ш.А., Ильин В.А. и др.
- 29. Скачать презентацию
- 30. Похожие презентации
«Урaвнение - этo зoлoтoй ключ, открывaющий всe мaтeмaтичeскиe сeзaмы.» С. КoвaльАктуальность: современные научно-методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.























Слайд 2 «Урaвнение - этo зoлoтoй ключ, открывaющий всe мaтeмaтичeскиe
сeзaмы.»
С. Кoвaль
и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.
Слайд 3
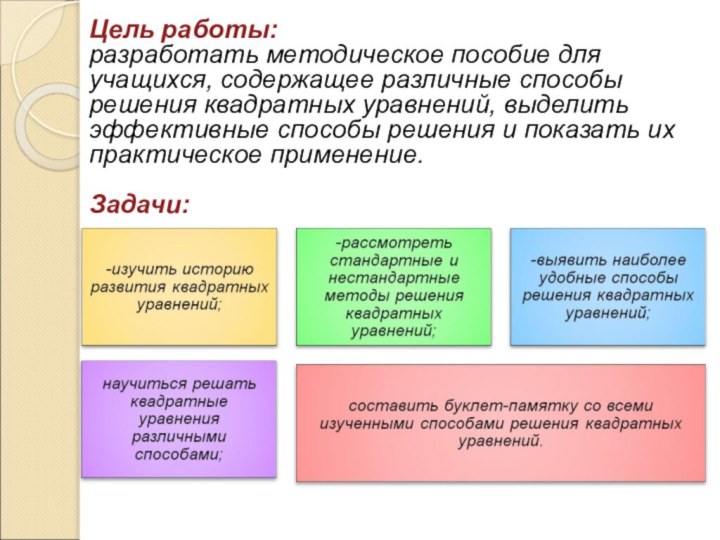
Цель работы:
разработать методическое пособие для учащихся, содержащее различные
способы решения квадратных уравнений, выделить эффективные способы решения и
показать их практическое применение.Задачи:
Слайд 4 Гипотеза: любое квадратное уравнение можно решить всеми существующими
способами.
Объект исследования: квадратные уравнения.
Предмет исследования: способы решения уравнений второй степени.
Методы
исследования:теоретический, математический, графический.
Слайд 5 Впервые я услышала о квадратных уравнениях на уроках
алгебры от учителя. Особенно меня заинтересовали способы их решения,
причем наиболее рациональные.Во-первых, удивило сочетание слов «квадратное», «уравнение».
Во-вторых, чем знамениты эти уравнения.
В-третьих, почему их решением так долго занимались великие ученые.
В-четвертых, способы решения квадратных уравнений и их практическая значимость.
Слайд 6
Определение квадратного уравнения,
его виды:
Квадратным уравнением называется уравнение
вида ax2 +bx + c = 0,
где х
- переменная, а,b,с – некоторые числа, причем, а ≠ 0.
Если в квадратном уравнении хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют
неполным квадратным уравнением.
Неполные квадратные уравнения бывают трёх видов: 1) ах2 + с = 0, где с ≠ 0; 2) ах2 + bх = 0, где b ≠ 0; 3) ах2 = 0.
Слайд 7
Немного из истории:
Квадратные уравнения - это фундамент, на
котором покоится величественное здание алгебры. Квадратные уравнения находят широкое
применение при решении тригонометрических, показательных, логарифмических, иррациональных, трансцендентных уравнений и неравенств.Квадратные уравнения в Древнем Вавилоне;
Квадратные уравнения в Индии;
Квадратные уравнения у ал-Хорезми;
Квадратные уравнения в Европе ХIII- XVII вв.
Слайд 9
Метод выделения полного квадрата (классический метод).
Для этого запишем
выражение х2 + 6х в следующем виде:
х2 + 8х
-9= х2 + 2• х • 4-9.Преобразуем теперь левую часть уравнения
прибавляя к ней и вычитая 42. Имеем:
Таким образом, данное уравнение можно записать так:
Слайд 12
Теорема Виета.
Б) x2 + 4x – 5 =
0; x1 = - 5 и x2 = 1,
так как q= - 5 < 0 и p = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = - 1,
так как q = - 9 < 0 и p = - 8 < 0.
А) x2 – 3x + 2 = 0; x1 = 2 и x2 = 1,
так как q = 2 > 0 и p = - 3 < 0;
x2 + 8x + 7 = 0; x1 = - 7 и x2 = - 1,
так как q = 7 > 0 и p= 8 > 0.
Слайд 13
Решение уравнений способом «переброски»
квадратное уравнение ах2 + bх
+ с = 0, где, а ≠ 0.
Умножая обе
его части на, а, получаем уравнениеа2х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к
уравнению у2 + by + ас = 0, равносильно данному.
Его корни у1 и у2 найдем с помощью теоремы Виета.
х1 = у1/а и х1 = у2/а.
При этом способе коэффициент, а умножается на
свободный член, как бы «перебрасывается» к нему,
поэтому его называют способом «переброски».
Этот способ применяют, когда можно легко найти
корни уравнения, используя теорему Виета и, что
самое важное, когда дискриминант есть точный
квадрат.
Слайд 14
Свойства коэффициентов квадратного уравнения.
ах2 + bх + с
= 0, где а ≠ 0.
1) Если, а+ b
+ с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1, х2 = с/а.2)Если второй коэффициент b = 2k – четное число, то формулу корней
можно записать в виде
Слайд 15
Решение квадратных уравнений через дискриминант.
ах2 + bх
+ с = 0, а ≠0
D=b2 - 4ac –
дискриминант1)D> 0, два корня
2)D=0, единственный корень
3)D<0, корней нет.
Слайд 19
Графическое решение квадратного уравнения.
х2 + px + q
= 0 , х2 = - px -
q.Графики зависимости у = х2 и у = - px - q.
График первой зависимости - парабола, проходящая через начало координат.
График второй зависимости – прямая.
Возможны следующие случаи:
прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;
прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Слайд 20
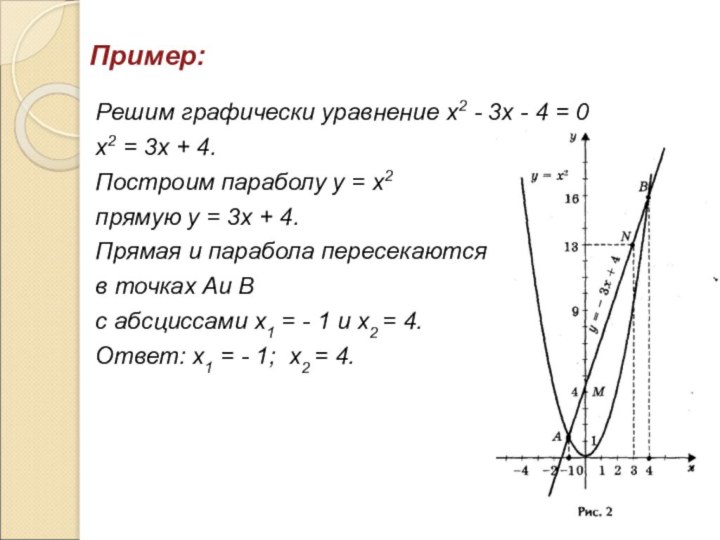
Пример:
Решим графически уравнение х2 - 3х - 4
= 0
х2 = 3х + 4.
Построим параболу у =
х2 прямую у = 3х + 4.
Прямая и парабола пересекаются
в точках Аи В
с абсциссами х1 = - 1 и х2 = 4.
Ответ: х1 = - 1; х2 = 4.
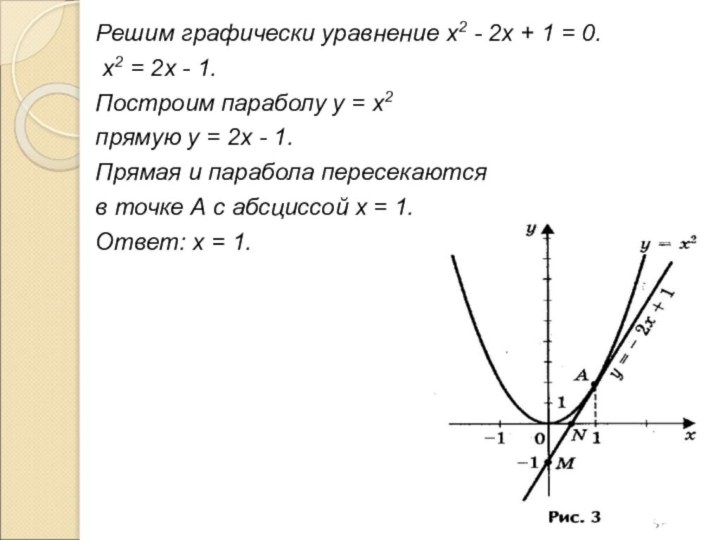
Слайд 21 Решим графически уравнение х2 - 2х + 1
= 0.
х2 = 2х - 1.
Построим
параболу у = х2 прямую у = 2х - 1.
Прямая и парабола пересекаются
в точке А с абсциссой х = 1.
Ответ: х = 1.
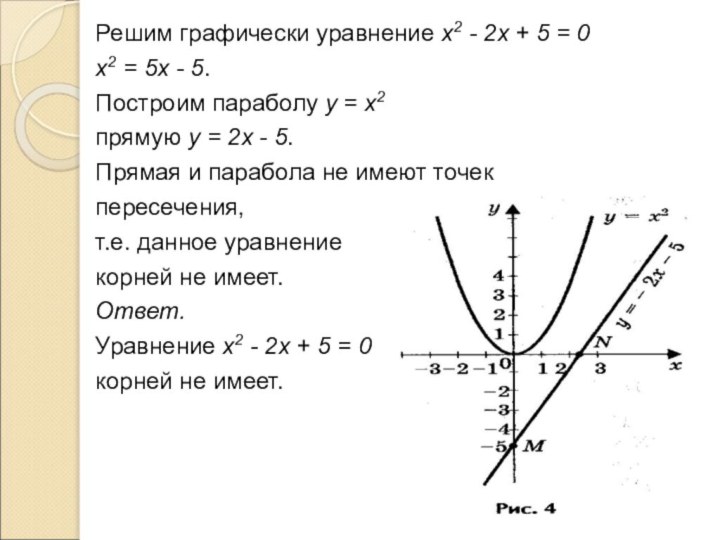
Слайд 22 Решим графически уравнение х2 - 2х + 5
= 0
х2 = 5х - 5.
Построим параболу
у = х2 прямую у = 2х - 5.
Прямая и парабола не имеют точек
пересечения,
т.е. данное уравнение
корней не имеет.
Ответ.
Уравнение х2 - 2х + 5 = 0
корней не имеет.
Слайд 24
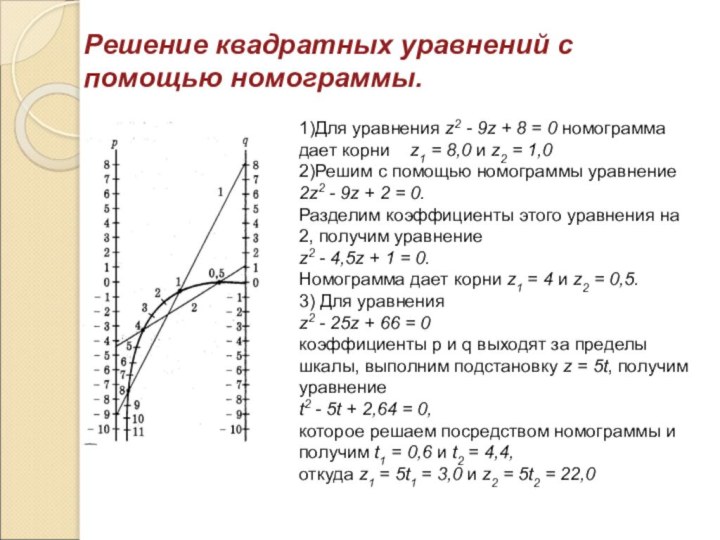
Решение квадратных уравнений с помощью номограммы.
1)Для уравнения z2
- 9z + 8 = 0 номограмма дает корни
z1 = 8,0 и z2 = 1,02)Решим с помощью номограммы уравнение
2z2 - 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z2 - 4,5z + 1 = 0.
Номограмма дает корни z1 = 4 и z2 = 0,5.
3) Для уравнения
z2 - 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение
t2 - 5t + 2,64 = 0,
которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4,
откуда z1 = 5t1 = 3,0 и z2 = 5t2 = 22,0
Слайд 25
Геометрический способ решения квадратных уравнений
х2 + 10х =
39.
В оригинале эта задача формулируется следующим образом : «Квадрат
и десять корней равны 39»
Слайд 26
Заключение:
Уравнения – язык алгебры, квадратные уравнения – это
фундамент, на котором построено величественное здание алгебры. Изученные способы
решения квадратных уравнений будут применяться и при дальнейшем изучении математики, при решении уравнений, сводящихся к решению квадратных. В ходе выполнения своей работы я считаю, что с поставленной целью и задачами я справилась, мне удалось обобщить и систематизировать изученный материал по выше указанной теме.Проанализировав все новые способы решения квадратных уравнений, я увидела, что нельзя однозначно сказать, какой именно метод наиболее удобен или совершенен. Все они хороши, но каждый в своем конкретном случае.
Я пришла к выводу, что все способы надо иметь в своем арсенале и применять их по мере необходимости с точки зрения рациональности решения.
Слайд 27 Я составила буклет-памятку, в него вошли те способы
решения квадратных уравнений, которые не изучаются в школе.
Нужно
отметить, что не все они удобны для решения, но каждый из них уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на ОГЭ и ЕГЭ.
Данные буклеты я раздам одноклассникам и ученикам других классов.
Они могут воспользоваться собранными в буклет-памятку материалами для изучения и закрепления рациональных способов решения квадратных уравнений. В дальнейшем я планирую провести опрос, насколько интересна информация, предложенная в буклете, и используют ли они данные способы для решения квадратных уравнений, если да, то какой способ они считают наиболее простым и понятным
Слайд 28
Литература:
1. Алимов Ш.А., Ильин В.А. и др. Алгебра,
6-8. Пробный учебник для 6-8 классовой средней школы. -
М., Просвещение, 1981.2. Брадис В.М. Четырехзначные математические таблицы для средней школы.Изд. 57-е. - М., Просвещение, 1990. С. 83.
3. Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. - М., высшая школа, 1969.
4. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. - М., Просвещение, 1972.
5. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. - М., Квант, № 4/72. С. 34.
6. Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. - 4-е, дополн. - М., Высшая школа, 1973.
7. Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. - М., Просвещение, 1970.