- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Интеграл
Содержание
- 2. «Путешествие в мир интегралов ипервообразных»
- 3. Достижения крупные людям Никогда не давались легко!Путешествие в мир интегралов и первообразных.
- 4. Цели и задачи: Обучающие: обобщение и систематизация
- 5. Верно ли утверждение, определение, свойство?1. Функция F
- 6. Устная работа. ;Существует ли интегралы:2;Назовите одну из
- 8. Немного истории -1675 г, опубликовано в 1686
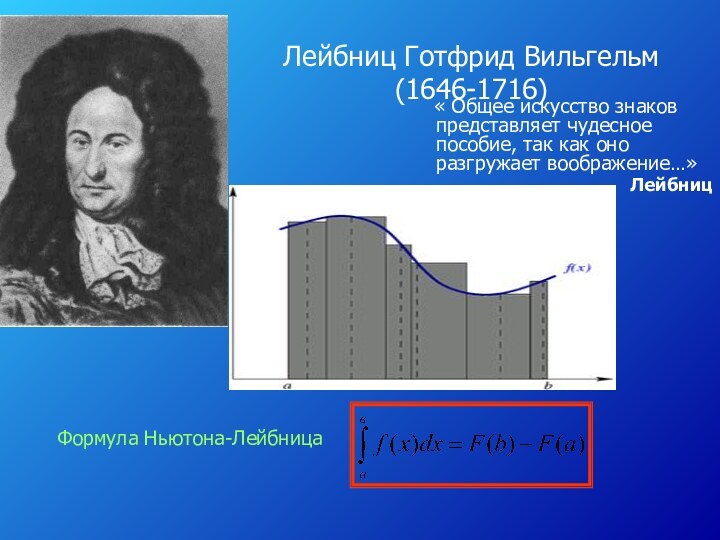
- 9. Лейбниц Готфрид Вильгельм (1646-1716) « Общее
- 10. Исаак Ньютон (1643-1727)Разумом он превосходил
- 11. Немного истории «Интеграл» придумал Я.Бернулли (1690)«восстанавливать» от латинского integro«целый» от латинского integer
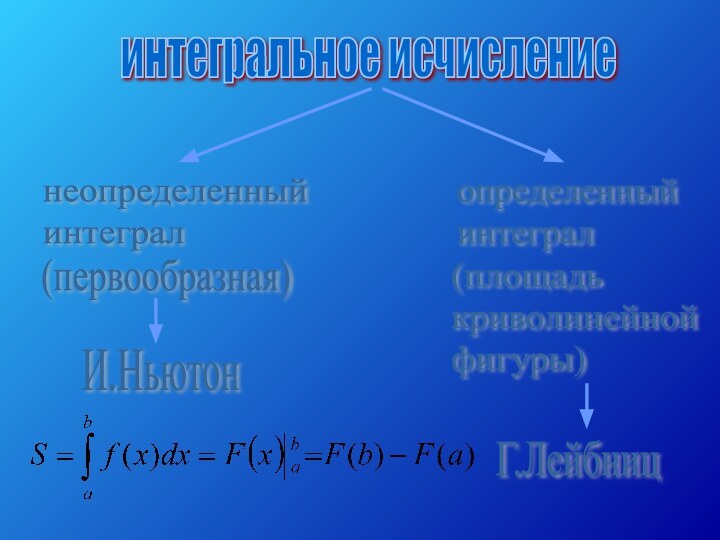
- 12. интегральное исчислениенеопределенный интегралопределенный интеграл(первообразная)(площадь криволинейной фигуры)И.НьютонГ.Лейбниц
- 13. ДифференцированиеИнтегрированиех(t)v(t)a(t)Интеграл функции — естественный аналог суммы последовательности.
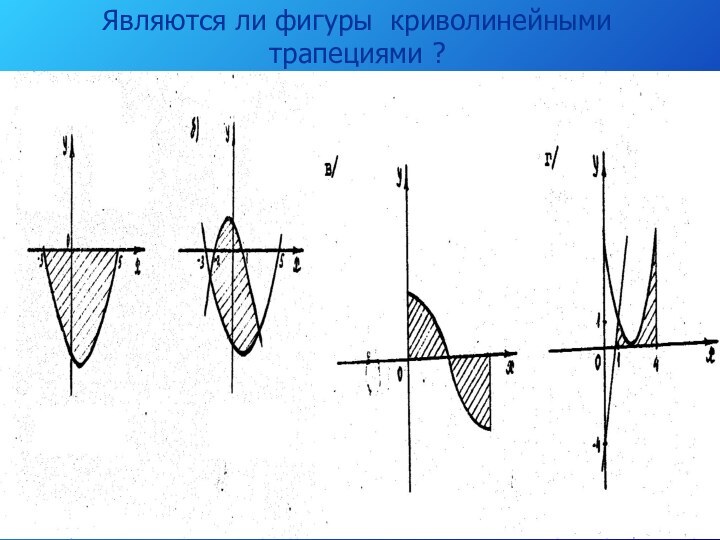
- 14. Являются ли фигуры криволинейными трапециями ?
- 15. Применение интегралаПлощадь фигурыОбъем тела вращенияРабота электрического зарядаРабота переменной силыЦентр масс
- 16. Скачать презентацию
- 17. Похожие презентации













Слайд 3
Достижения крупные людям
Никогда не давались легко!
Путешествие в мир
интегралов и первообразных.
Слайд 4
Цели и задачи:
Обучающие:
обобщение и систематизация знаний
учащихся;
закрепление основных понятий базового уровня.
Развивающие:
развитие познавательного
интереса; развитие логического мышления и внимания;
формирование потребности в приобретении знаний.
Воспитательные:
воспитание сознательной дисциплины и норм поведения;
воспитание ответственности, умения принимать самостоятельные решения.
Слайд 5
Верно ли утверждение, определение, свойство?
1. Функция F называется
первообразной для функции f на заданном промежутке, если для
всех х из этого промежутка F‘(х)=f(х)2. Если F‘(х)=0 на некотором промежутке I, то функция F не всегда постоянна на этом промежутке.
3. Пусть на отрезке [а; в] оси Ох задана непрерывная функция f, не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [а; в] и прямыми х=а и х=в называют криволинейной трапецией
5.Официальной датой рождения дифференциального исчисления можно считать май 1684, когда Лейбниц опубликовал первую статью «Новый метод максимумов и минимумов…». Эта статья в сжатой и малодоступной форме излагала принципы нового метода, названного дифференциальным исчислением.
4.Для любой непрерывной на отрезке [а;в] функции f Sn при n -> ∞ стремится к некоторому числу. Это число называют (по определению) интегралом функции f от а до в и обозначают
Слайд 6
Устная работа.
;
Существует ли интегралы:
2
;
Назовите одну из первообразных
для каждой из следующих функций:
f(x) = 4; f(x)=-1; f(x)=x³;
f(x)=cosx; f(x)=x²+3cosx.2
.
Слайд 8
Немного истории
-1675 г, опубликовано в 1686 г
ввел Г.Лейбниц
-
1675 г, Ж Лагранж
Официальной датой рождения дифференциального исчисления можно
считать май 1684, когда Лейбниц опубликовал первую статью «Новый метод максимумов и минимумов…» В XIX веке Коши первым дал анализу твёрдое логическое обоснование, введя понятие предела последовательности, он же открыл новую страницу комплексного анализа. Пуассон, Лиувилль, Фурье и другие изучали дифференциальные уравнения в частных производных и гармонический анализ.





























