Слайд 2
Введение
Если зависимость y(x) представлена рядом табличных отсчетов yi(xi),
то интерполяция значений y(x) – это вычисление значений y(x)
при заданном x, расположенном в интервале между отсчетами.
За пределами общего интервала определения y(x) , вычисление y(x) называют экстраполяцией (предсказанием значений функции).
Аппроксимация в системах компьютерной математики – это получение приближенных значений какого - либо выражения.
Слайд 3
Повестка дня
Список изучаемых разделов:
Интерполяция и ее виды.
Особенности аппроксимации
функций.
Методы интерполяции и аппроксимации.
Примеры решения задач интерполяции и
аппроксимации в Maple
Время, отводимое на каждый раздел: 5-10 минут.
Слайд 4
Обзор
Разделы лекции
Интерполяция и ее виды
Особенности аппроксимации функций
Методы интерполяции
и аппроксимации
Примеры решений задач интерполяции и аппроксимации в Maple
Слайд 5
Словарь терминов
Интерполирующая функция – это функция F(x), которая
принадлежит известному классу и принимает в узлах интерполяции те
же значения, что и искомая y(x).
Узлы интерполяции y(x)– это значения x в интервале [a, b] определения данной функции y(x), которые однозначно определены.
Слайд 6
Интерполяция и ее виды
Основная задача интерполирования.
На отрезке [a,
b] заданы n+1 точки x0, x1, … xi, …
xn (узлы интерполяции) и значения функции y(x) в этих точках y(x0) = y0, y(x1) = y1, … y(xi) = yi, … y(xn) = yn .
Требуется определить интерполирующую функцию F(x), которая:
Относится к известному классу,
Принимает в узлах интерполяции те же значения, что и y(x): F(x0) = y0, F(x1) = y1, … F(xi) = yi, … F(xn) = yn .
Слайд 7
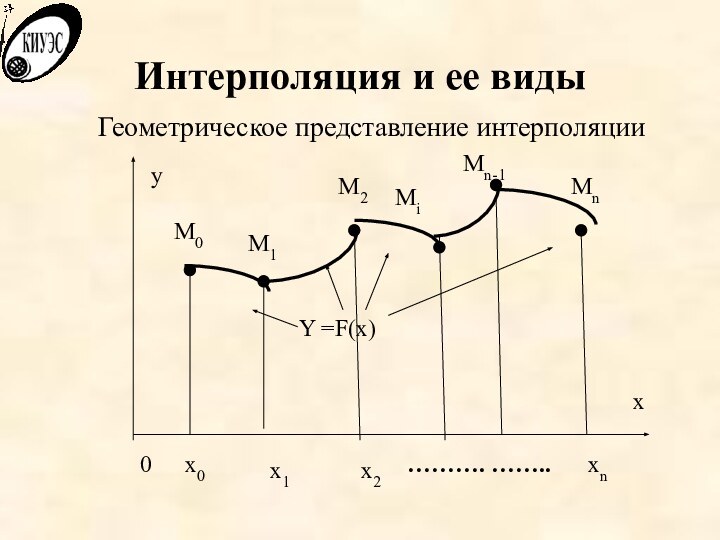
Интерполяция и ее виды
Геометрическое представление:
Найти кривую y =
F(x) определенного типа, проходящую через заданную систему точек
M(xi,
yi), где I =0,1,2,..n.
В общем случае задача является неопределенной.
Однако она становится однозначной, если вместо произвольной функции F(x) искать, например, полином Pn(x) степени, удовлетворяющий условиям Pn (x0) = y0, Pn(x1) = y1, … Pn (xi) = yi, … Pn (xn) = yn .
Слайд 8
Интерполяция и ее виды
Геометрическое представление интерполяции
0
x0
x1
x2
xn
x
y
Mi
M0
M1
M2
Mn
Mn-1
………. ……..
Y =F(x)
Слайд 9
Интерполяция и ее виды
Основные виды интерполяционных полиномов:
Канонический полином,
Полином
Ньютона,
Полином Лангранжа,
Полином Эйткена,
Полином Чебышева.
Слайд 10
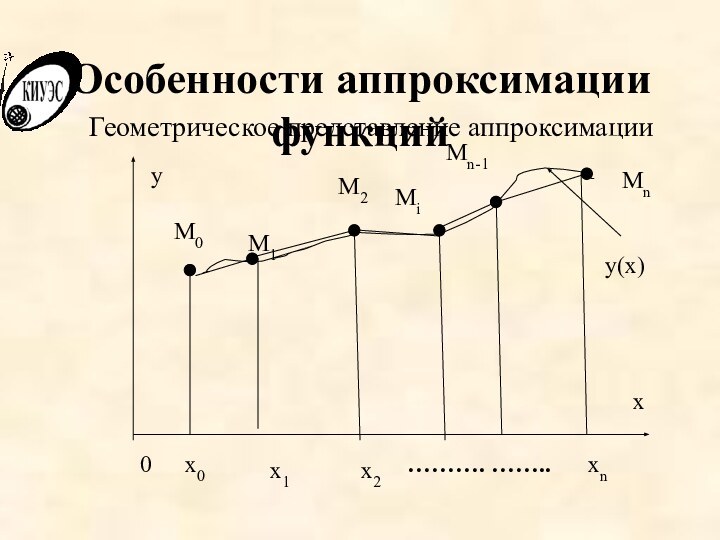
Особенности аппроксимации функций
Под аппроксимацией функциональных зависимостей подразумевается получение
некоторой конкретной функции, вычисленные значения которой с некоторой точностью
аналогичны аппроксимируемой зависимости. Обычно предпочитают найти одну зависимость, которая дает точное значение искомой функции y(x) в узловых точках в пределах погрешности вычислений по умолчанию. Для этого также используют степенные многочлены - полиномы или линейные функции.
Слайд 11
Особенности аппроксимации функций
Геометрическое представление аппроксимации
0
x0
x1
x2
xn
x
y
Mi
M0
M1
M2
Mn
Mn-1
………. ……..
y(x)
Слайд 12
Методы интерполяции и аппроксимации
Полиномиальные
Сплайновые
Линейные
Рациональные (отношение двух полиномов)
Метод
наименьших квадратов
Тригонометрические (рядами Фурье).
Слайд 13
Примеры решений задач интерполяции и аппроксимации в Maple
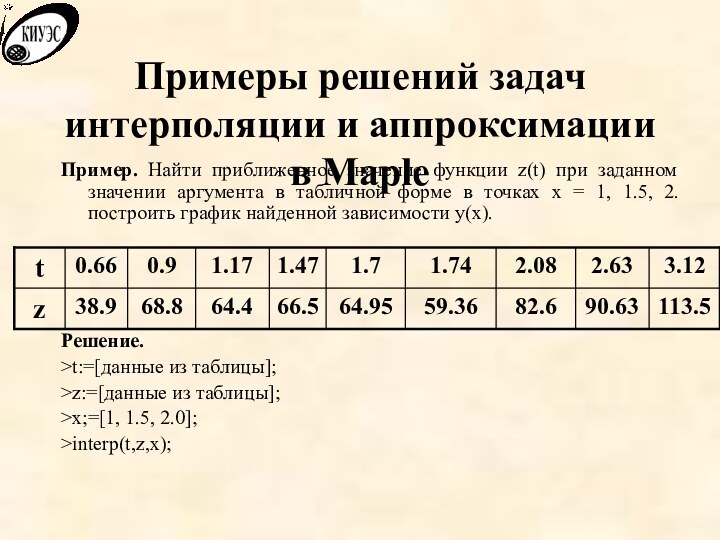
Пример.
Найти приближенное значение функции z(t) при заданном значении аргумента
в табличной форме в точках x = 1, 1.5, 2. построить график найденной зависимости y(x).
Решение.
>t:=[данные из таблицы];
>z:=[данные из таблицы];
>x;=[1, 1.5, 2.0];
>interp(t,z,x);
Слайд 14
Примеры решений задач интерполяции и аппроксимации в Maple
>z:=y→interp(t,z,x);
>for
i from 1 to 3 do x[i]:=z(x[i]); end do;
>l:=[[t[n],
z[n] Sn=1..9];
> plot(l,z(y)], y=0.66..3.12,style=[point, line], symbol=circle)
Задача сплайн-интерполяции
Используется функция spline(X, Y, x, method), где параметр method определяет вид сплайна.
В качестве данного параметра используются ключевые слова linear, quadratic, cubic, quadric или числа 1,2 3, 4. Если параметр не указан, то используется кубический сплайн.
Слайд 15
Примеры решений задач интерполяции и аппроксимации в Maple
Решение
:
> spline(t, z, y);
> zs:=y → spline(t, z, y);
>
for I from 1 to 3 do xs[i]:=zs(x[i]); end do;
ZSL:=y → spline(t, z, y, l);
> l:=[[t[n], z[n] Sn=1..9];
> plot(l, zs(y), zsl(y)], y=0.66..3.12, style [point, line, line], symbol=circle)





![Интерполяция и аппроксимация Интерполяция и ее виды Основная задача интерполирования.На отрезке [a, b] заданы n+1](/img/tmb/12/1169973/12201340dde1bc048394744a328a46e2-720x.jpg)