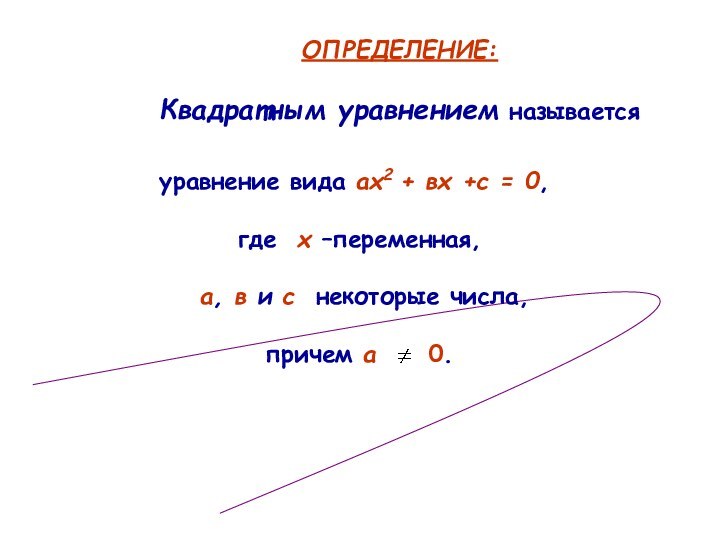
где х –переменная,
а, в и с
некоторые числа,причем а 0.
ОПРЕДЕЛЕНИЕ:
Квадратным уравнением называется
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Квадратные уравнения алгебра 8 класс
Содержание
- 2. уравнение вида ах2 + вх +с =
- 3. ПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯНЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯКВАДРАТНЫЕ УРАВНЕНИЯа ≠
- 4. 1 варианта) 6х2
- 5. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙв=0ах2+с=0с=0ах2+вх=0в,с=0ах2=0 1.Перенос с
- 6. РЕШИ НЕПОЛНЫЕ УРАВНЕНИЯ :1 вариант:
- 7. Проверь товарища
- 8. Динамическая паузаа) 3х2 – 5х - 2
- 9. Способы решения полных квадратных уравненийВыделение квадрата двучлена.Формула: D = b2- 4ac, x1,2=Теорема Виета.
- 10. От чего зависит количество корней квадратного уравнения?Ответ:
- 11. Вычисли дискриминант и определи количество корней квадратного
- 12. Проверь товарища D=b2-4ac
- 13. РЕШИ УРАВНЕНИЯ с помощью формулы :
- 14. Проверь себя 1 вариант2х2
- 15. Исторические сведения:Квадратные уравнения впервые встречаются в работе
- 16. Решение задачи Бхаскары: Пусть было х
- 17. Скачать презентацию
- 18. Похожие презентации
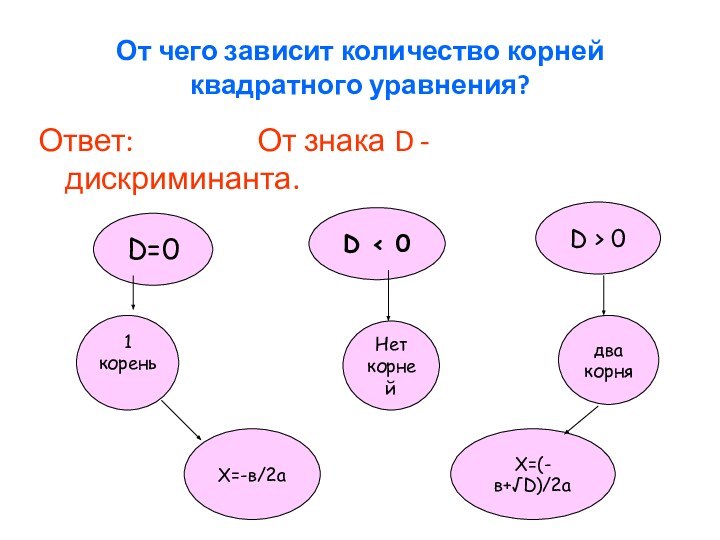
уравнение вида ах2 + вх +с = 0, где х –переменная, а, в и с некоторые числа, причем а 0.ОПРЕДЕЛЕНИЕ: Квадратным уравнением называется
Слайд 2
уравнение вида ах2 + вх +с = 0,
причем а 0.
Слайд 3
ПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
НЕПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
КВАДРАТНЫЕ УРАВНЕНИЯ
а ≠ 0, в ≠
0, с ≠ 0
а ≠ 0, в =
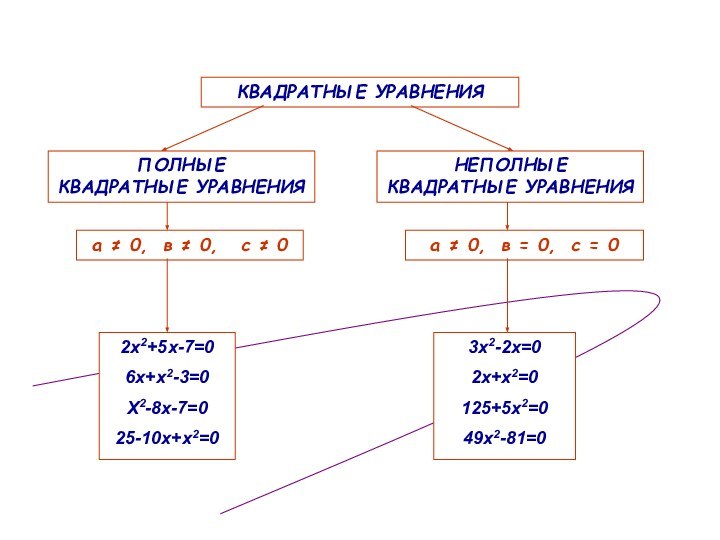
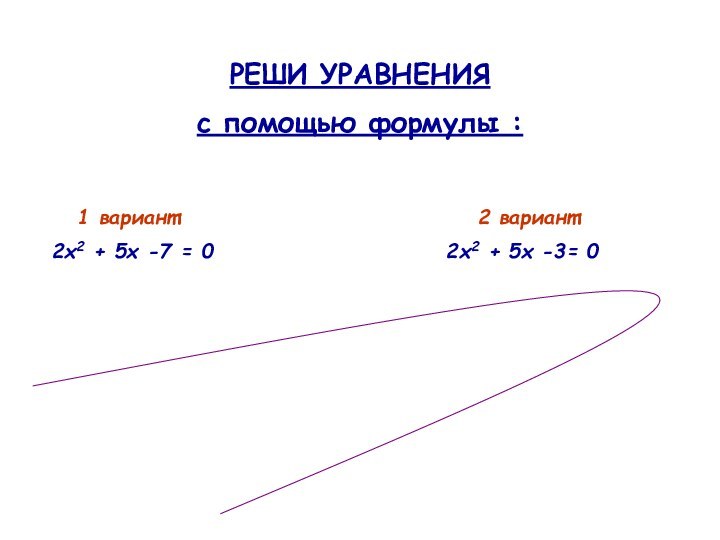
0, с = 02х2+5х-7=0
6х+х2-3=0
Х2-8х-7=0
25-10х+х2=0
3х2-2х=0
2х+х2=0
125+5х2=0
49х2-81=0
Слайд 4
1 вариант
а) 6х2 –
х + 4 = 0
б) 12х - х2
= 0в) 8 + 5х2 = 0
2 вариант
а) х – 6х2 = 0
б) - х + х2 – 15 = 0
в) - 9х2 + 3 = 0
1 вариант
а) а = 6, в = -1, с = 4;
б) а = -1, в = 12, с = 0;
в) а = 5, в = 0, с = 8;
2 вариант
а) а = -6, в =1, с = 0;
б) а = 1, в =-1, с = -15;
в) а = -9, в = 0, с = 3.
Определите коэффициенты
квадратного уравнения:
Слайд 5
РЕШЕНИЕ
НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0
ах2+с=0
с=0
ах2+вх=0
в,с=0
ах2=0
1.Перенос с в
правую часть уравнения.
ах2= -с
2.Деление обеих частей уравнения на а.
х2=
-с/а3.Если –с/а>0 -два решения:
х1 = и х2 = -
Если –с/а<0 - нет решений
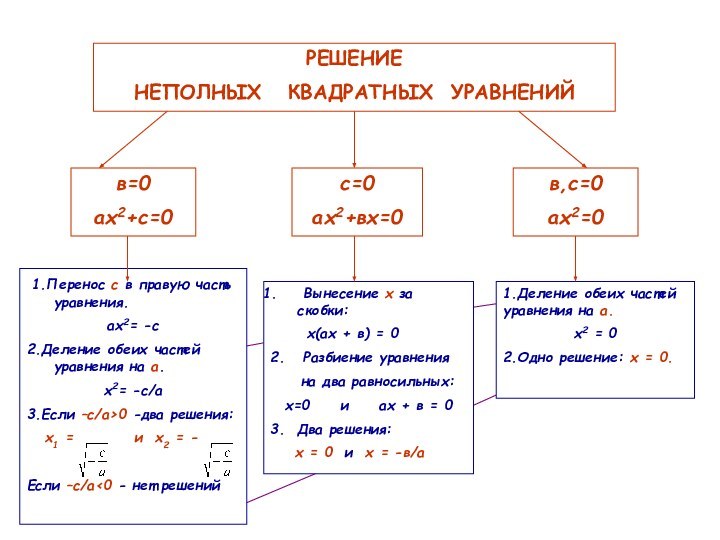
Вынесение х за скобки:
х(ах + в) = 0
2. Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.
Слайд 6
РЕШИ НЕПОЛНЫЕ УРАВНЕНИЯ :
1 вариант:
2 вариант:
а) 2х + 3х2= 0 а) 3х2 – 2х = 0
б) 3х2 – 243= 0 б) 125 - 5х2 = 0
в) 6х2 = -10х – 2х( 5 – 3х). в) -12х – 6х(2 – 3х) = 18х2
Слайд 7
Проверь товарища
1
вариант
а) х(2+3х)=0,
х=0 или 2+3х =0,
3х = -2,х= -2/3.
Ответ: 0 и -2/3.
б) 3х2 = 243,
х2 = 243/3,
х2 = 81,
х =-9, х= 9.
Ответ: -9 и 9.
в) 6х2 = - 10х -10х + 6х2,
6х2 +10х +10х - 6х2 =0,
20х = 0,
х=0.
Ответ: 0.
2 вариант
а) х(3х -2) =0,
х=0 или 3х-2 =0,
3х = 2,
х = 2/3.
Ответ: 0 и 2/3.
б) - 5х2 = - 125,
х2 = -125/-5,
х2 = 25,
х = - 5, х = 5.
Ответ: -5 и 5.
в) - 12х -12х +18 х2 - 18 х2 = 0,
- 24х = 0,
х = 0.
Ответ: 0.
Слайд 8
Динамическая пауза
а) 3х2 – 5х - 2 =
0
б) 4х2 – 4х + 1= 0
в) х2 –
2х +3 = 0г) 6х2 – х + 4 = 0
д) 12х - х2 = 0
е) 8 + 5х2 = 0
ж) 5х2 – 4х + 2 = 0
з) 4х2 – 3х -1= 0
и) х2 – 6х + 9= 0
к) х – 6х2 = 0
л) - х + х2 – 15 = 0
м) - 9х2 + 3 = 0
Слайд 9
Способы решения
полных квадратных уравнений
Выделение квадрата двучлена.
Формула: D
= b2- 4ac, x1,2=
Теорема Виета.
Слайд 11
Вычисли дискриминант и определи количество корней квадратного уравнения
1 вариант
а) 3х2 – 5х -
2 = 0б) 4х2 – 4х + 1= 0
в) х2 – 2х +3 = 0
2 вариант
а) 5х2 – 4х + 2 = 0
б) 4х2 – 3х -1= 0
в) х2 – 6х + 9= 0
Слайд 12
Проверь товарища D=b2-4ac
1 вариант
а) D =(-5)2 - 4*3*(-2) = 49,
2 корня;б) D =(-4)2 - 4*4*1 = 0,
1 корень;
в) D =(-2)2 - 4*1*3 = -8,
нет корней
2 вариант
а) D =(-4)2 - 4*5*2 = -24,
нет корней;
D =(-3)2 - 4*4*(-1) = 25,
2 корня;
D =(-6)2 - 4*1*9 = 0,
1 корень
Слайд 14
Проверь себя
1 вариант
2х2 +
5х -7 = 0,
D =52 - 4*2* (-7)= 81
= 92,х = (-5 -9)/2*2=-14/4=- 3,5,
х =(-5 +9)/4=4/4=1.
Ответ: -3,5 и 1.
2 вариант
2х2 + 5х -3= 0,
D = 52 – 4*2* (-3)= 49 = 72,
х = (-5 -7)/2*2=-12/4= -3,
х = (-5 +7)/4= 2/4= 0,5.
Ответ: -3 и 0,5.
Слайд 15
Исторические сведения:
Квадратные уравнения впервые встречаются в работе индийского
математика и астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в)
изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму.
________________________________________________
Вот задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?
Слайд 16 Решение задачи Бхаскары: Пусть было х обезьянок, тогда
на поляне забавлялось – ( х/8)2 и 12 прыгали
по лианам. Составим уравнение:( х/8)2 + 12 = х,
х2/64 + 12 – х =0, /*64
х2 - 64х + 768 = 0,
D = (-64)2-4*1*768 =4096 – 3072 = 1024 = 322, 2 корня
х= (64 -32)/2 = 16,
х= (64 + 32)/2 = 48.
Ответ: 16 или 48 обезьянок.
