- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Вводное повторение (8 класс)
Содержание
- 2. Как появилась алгебра Алгебра
- 3. Темы повторения:Глава I. Выражения, тождества, уравнения.Глава II.
- 4. Глава I. Выражения, тождества, уравнения 1. Заполните
- 5. Глава I. Выражения, тождества, уравнения Равенство, содержащее
- 6. Глава I. Выражения, тождества, уравненияРешите уравнение:
- 7. А знаете ли Вы, что первое счётное
- 8. Глава II. ФункцииЗависимость одной переменной от другой
- 9. О функциях В первой половине 17
- 10. Какие из указанных функций мы изучали?
- 12. Глава II. ФункцииЧастный случаем линейной функции является прямая пропорциональность.
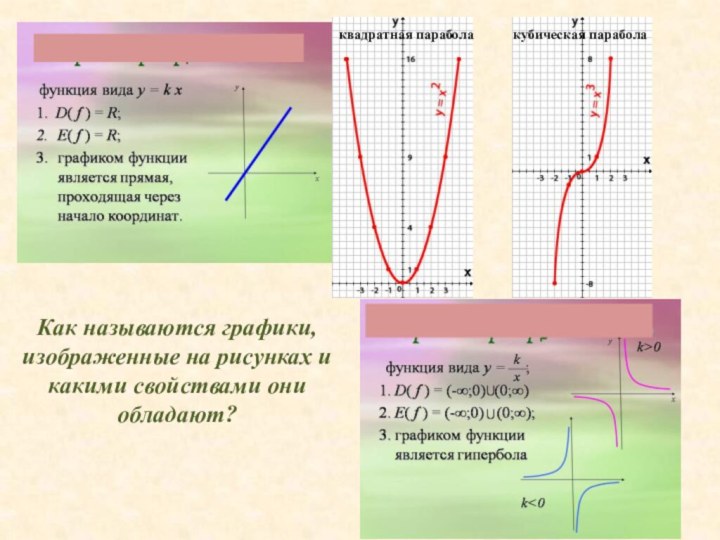
- 13. Как называются графики, изображенные на рисунках и какими свойствами они обладают?квадратная параболакубическая парабола
- 14. Постройте графики следующих функций:а) y = 2x+3б)
- 15. Глава III. Степень с натуральным показателем
- 16. Глава III. Степень с натуральным показателемИспользуя свойства
- 17. Глава IV. Многочлены
- 18. Глава IV. Многочлены Выполните умножение: Если все
- 19. Глава V. Формулы сокращенного умноженияСформулируйте тождества сокращенного
- 20. Линейным уравнением с двумя переменными называется уравнение
- 21. Глава VI . Системы линейных уравненийПара значений
- 22. Глава VI . Системы линейных уравненийГрафический метод
- 23. Глава VI . Системы линейных уравненийМетод алгебраического
- 24. Глава VI . Системы линейных уравненийРешите системы:графически: методом подстановки: методом сложения:
- 25. Скачать презентацию
- 26. Похожие презентации
























Слайд 3
Темы повторения:
Глава I. Выражения, тождества, уравнения.
Глава II. Функции.
Глава
III. Степень с натуральным показателем.
Глава IV. Многочлены.
Глава V. Формулы
сокращенного умножения.Глава VI . Системы линейных уравнений.
Слайд 4
Глава I. Выражения, тождества, уравнения
1. Заполните таблицу:
Какими числами
являются соответственные значения
выражений 3х-1 и
– 3х+1 ?2. Какие из данных равенств не являются тождеством?
–7
7
– 4
4
– 1
1
2
– 2
5
– 5
11
– 11
14
– 14
Какое равенство называется тождеством?
Счет и вычисления - основа порядка в голове.
(Песталоцци)
Слайд 5
Глава I. Выражения, тождества, уравнения
Равенство, содержащее переменную называют
уравнением с одним неизвестным (переменной).
Корнем уравнения называют
значение переменной,при котором уравнение обращается в верное
равенство.
Решить уравнение – значит найти его корни или
доказать, что корней нет.
Уравнение вида ax=b, где х – переменная,
a и b – некоторые числа, называют линейным
уравнением с одной переменной.
Слайд 6
Глава I. Выражения, тождества, уравнения
Решите уравнение:
Правила
раскрытия скобок:
1) если перед скобками стоит знак плюс,
то можно опустить скобки, сохранив знаки слагаемых, стоящих в скобках.
2) Если перед скобками стоит знак минус, то можно опустить
скобки, изменив знаки всех слагаемых, стоящих в скобках
на противоположный.
3) Число, стоящее за скобками умножается на каждое
слагаемое, стоящее в скобках.
Слайд 7 А знаете ли Вы, что первое счётное устройство
— абак?
Первыми «вычислительными устройствами», которыми
пользовались в древности люди, были пальцы рук и камешки. Позднее появились бирки с зарубками и верёвки с узелками.
В Древнем Египте и Древней Греции задолго до нашей эры использовали абак – доску с полосками, по которым продвигались камешки. Это было первое устройство, специально предназначенное для вычислений. Со временем абак совершенствовали – в римском абаке камешки или шарики передвигались по желобкам. Абак просуществовал до 18 века, когда его
заменили письменные вычисления.
Русский абак – счёты появились в 16 веке.
Ими пользуются и в наши дни. Большое преимущество
русских счётов в том, что они основаны на
десятичной системе счисления, а не на
пятеричной, как все остальные абаки.
Слайд 8
Глава II. Функции
Зависимость одной переменной от другой называют
функциональной зависимостью или функцией, если каждому
значению независимой переменной
соответствует единственное значение зависимой переменной.
Все значения, которые принимает независимая переменная, образуют область определения функции.
Значения зависимой переменной называют значениями функции.
Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Слайд 9
О функциях
В первой половине 17 века
в связи с развитием механики в математику идеи изменения
и движения. Термин «функция» впервые ввел немецкий математик Г. Лейбниц. У него функция связывалась с геометрическим образом (графиком). В дальнейшем функцию рассматривают как аналитическое выражение.Слайд 13 Как называются графики, изображенные на рисунках и какими
свойствами они обладают?
квадратная парабола
кубическая парабола
Слайд 15
Глава III. Степень с натуральным показателем
Степенью числа с натуральным
показателем, называют выражение , равное произведению
множителей, каждый из которых равен .
Свойства степени:
Слайд 16
Глава III. Степень с натуральным показателем
Используя свойства выполните
упражнения:
Запишите одночлен в стандартном виде:
Принадлежит ли графику
функции точка:
Слайд 17
Глава IV. Многочлены
Многочленом называется сумма одночленов. Одночлены,
входящие в состав многочлена, называют его членами. Членами многочлена 4x2у – 3ab являются 4x2y и – 3ab . Если многочлен состоит из двух членов, то его называют двучленом: 15х5y – 7а3b4; y +20m ; 14a3+13a2. Если из трех – трехчленом: 5x3y – 7a3b4+5; y+5b4 – 3x3; 7a2+13a4+5ab2.
Чтобы умножить одночлен на многочлен, нужно умножить этот
одночлен на каждый член многочлена и полученные
произведения сложить.
Чтобы умножить многочлен на многочлен, нужно каждый
член одного многочлена умножить на каждый член
другого многочлена и полученные произведения сложить.
Слайд 18
Глава IV. Многочлены
Выполните умножение:
Если все одночлены в
многочлене приведены к стандартному виду и среди них нет подобных,
то говорят, что это многочлен стандартного вида. нестандартный вид стандартный вид 5x2yx – 7xyx 2+5axa = 5a2x – 2x3y .Разложите на множители многочлен:
Решите уравнение:
Слайд 19
Глава V. Формулы сокращенного умножения
Сформулируйте тождества сокращенного умножения
и используя их выполните преобразования.
Представьте в виде многочлена:
;
;
;
Решите уравнения:
Слайд 20 Линейным уравнением с двумя переменными называется уравнение вида
- переменные,
- некоторые числа.
Глава VI . Системы линейных уравнений
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Слайд 21
Глава VI . Системы линейных уравнений
Пара значений (х;у),
которая одновременно является решением каждого из уравнений системы, называют
решением системы.Методы решения систем линейных уравнений:
1) графический метод;
2) метод подстановки;
3) метод алгебраического сложения.
Слайд 22
Глава VI . Системы линейных уравнений
Графический метод решения.
С его помощью можно сделать следующие выводы:
построить в одной
системе координат графики уравнений:графиками обоих уравнений системы являются прямые;
эти прямые могут пересекаться (только в одной точке) – система имеет
единственное решение;
эти прямые могут быть параллельны – система несовместима – нет решений;
эти прямые совпадают – система неопределенна – система имеет
бесчисленное множество решений.
Метод подстановки.
Выразить из какого – нибудь уравнения системы одну переменную через другую;
подставить полученное выражение в другое уравнение;
решить полученное уравнение;
найди соответствующее значение второй переменной.
Записать ответ в виде пары значений (х; у) .
Слайд 23
Глава VI . Системы линейных уравнений
Метод алгебраического сложения.
уравнивают коэффициенты при одной из переменных;
складывают (или вычитают)
левые и правые части уравнений системы;решают получившееся уравнение с одной переменной;
находят соответствующее значение второй переменной.
Записывают ответ в виде пары значений (х; у).





























