- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Интерполирование функций
Содержание
- 2. Постановка задачи:
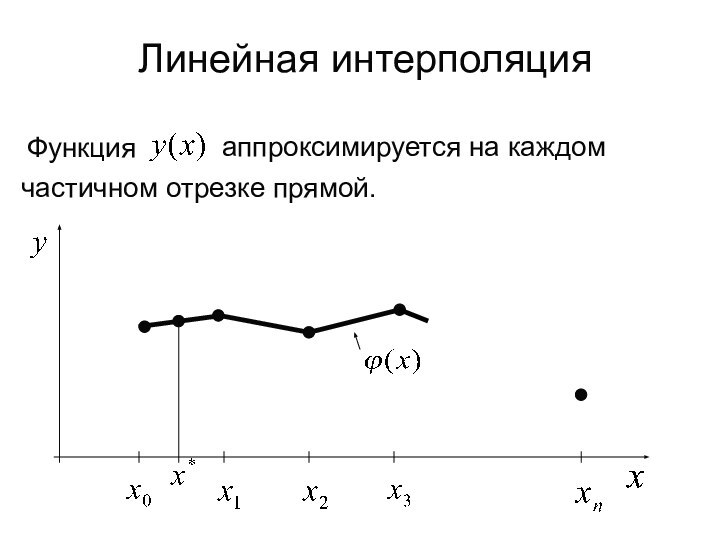
- 3. Постановка задачи:Построим функцию -интерполяционную функцию, удовлетворяющую условию:- условие интерполяциитогдасчитать
- 4. Функцияаппроксимируется на каждомчастичном отрезке прямой. Линейная интерполяция
- 5. Расчетные формулы линейной интерполяции(4)(5)
- 6. Квадратичная интерполяция- условие интерполирования
- 7. Получение расчетных формул- неизвестные переменные(6)- определитель Вандермонда
- 8. Алгоритм1. Определить отрезок ,содержащий 2. Решить систему
- 9. Глобальная интерполяция алгебраическими многочленами(7)(8)(8) – СЛАУ из
- 10. Интерполяционный многочлен Лагранжа(1)- многочлены n-ой степени- значения функций из таблицы(2)- условия интерполирования
- 11. Построение многочленов сi(x) (3)
- 12. (4)(5)(6)Построение многочленов сi(x) (продолжение)
- 13. Вид интерполяционного многочлена Лагранжа(7)(8)(9)
- 14. Запись интерполяционного многочлена Лагранжа через (10)(11)(12)
- 15. Частные случаи интерполяционного многочлена Лагранжаа) линейная интерполяция через точки (xi,yi), (xi+1,yi+1)
- 16. б) квадратичная интерполяция через точки (xi-1,yi-1),(xi,yi), (xi+1,yi+1)
- 17. Погрешность интерполирования- остаточный член формулы ЛагранжаФункцияимеет (n+1) нулей следовательно, (n+2) нуля(13)(14)Пустьобозн.требуем
- 18. Погрешность интерполирования (продолжение)Из (13) получим, что
- 19. Верхняя оценка погрешности rn(x)(15)
- 20. Сходимость интерполяционного процессаОпределение: равномерная сходимость означает, что
- 21. Интерполяционная формула Ньютона Разделенными разностями первого порядка
- 22. Таблица разделенных разностей
- 23. Скачать презентацию
- 24. Похожие презентации
Постановка задачи: Функция задана таблично:Вычислить: -сетка или узлы интерполирования(2)(1)






















Слайд 3
Постановка задачи:
Построим функцию
-интерполяционную функцию,
удовлетворяющую условию:
- условие
интерполяции
тогда
считать
Слайд 8
Алгоритм
1. Определить отрезок
,содержащий
2. Решить систему (6),
для определения:
3. Подставить
в функцию
при известных
коэффициентах
a
Слайд 9
Глобальная интерполяция алгебраическими многочленами
(7)
(8)
(8) – СЛАУ из (n+1)
уравнения с определителем
Вандермонда
(7) существует и единственно
- условие интерполирования
Слайд 10
Интерполяционный многочлен Лагранжа
(1)
- многочлены n-ой степени
- значения функций
из таблицы
(2)
- условия интерполирования
Слайд 15
Частные случаи интерполяционного многочлена Лагранжа
а) линейная интерполяция через
точки (xi,yi), (xi+1,yi+1)
Слайд 17
Погрешность интерполирования
- остаточный член формулы Лагранжа
Функция
имеет (n+1) нулей
следовательно, (n+2) нуля
(13)
(14)
Пусть
обозн.
требуем
Слайд 20
Сходимость интерполяционного процесса
Определение: равномерная сходимость означает, что
при
Определение:
говорят, что интерполяционный процесс для функции y(x) сходится в
точке ,если существует
Слайд 21
Интерполяционная формула Ньютона
Разделенными разностями первого порядка называются
отношения:
По разделенным разностям первого порядка можно построить разделенные
разности второго порядка: (1)
(2)