Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Множества

Содержание

2. МНОЖЕСТВОЭЛЕМЕНТ МНОЖЕСТВАСПОСОБЫ ЗАДАНИЯ МНОЖЕСТВПОДМНОЖЕСТВОПЕРЕСЕЧЕНИЕ МНОЖЕСТВОБЪЕДИНЕНИЕ МНОЖЕСТВВЫЧИТАНИЕ МНОЖЕСТВДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВвыход
3. Понятие множества — простейшее математическое понятие, оно
4. Элементы множества Объекты, из которых образовано множество,
5. Способы задания множеств А = {3, 4,
6. Характеристическое свойство Характеристическое свойство – это такое
7. подмножество Множество В является подмножеством множества А
8. Круги Эйлера Круги Эйлера – это особые
9. пересечение множеств Пересечение множеств — множество, состоящее
10. Объединение множеств Объединением множеств А и В
11. Вычитание множеств Разностью множеств А и В
12. Декартово произведение множеств Декартовым произведением множеств А
13. Изображение декартова произведения при помощи графа и таблицы А = {1, 2, 3}В = {3, 5}АВ1.2.3..3.5графтаблица
14. Скачать презентацию
15. Похожие презентации

МНОЖЕСТВОЭЛЕМЕНТ МНОЖЕСТВАСПОСОБЫ ЗАДАНИЯ МНОЖЕСТВПОДМНОЖЕСТВОПЕРЕСЕЧЕНИЕ МНОЖЕСТВОБЪЕДИНЕНИЕ МНОЖЕСТВВЫЧИТАНИЕ МНОЖЕСТВДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВвыход

Понятие множества — простейшее математическое понятие, оно не определяется, а лишь поясняется

Элементы множества Объекты, из которых образовано множество, называются элементами.Элементы множества принято обозначать

Способы задания множеств А = {3, 4, 5, 6}Множество А двузначных чисел:

Характеристическое свойство Характеристическое свойство – это такое свойство, которым обладает каждый элемент,

подмножество Множество В является подмножеством множества А (В ⊂ А), если каждый

Круги Эйлера Круги Эйлера – это особые чертежи, при помощи которых наглядно

пересечение множеств Пересечение множеств — множество, состоящее из всех тех элементов, которые

Объединение множеств Объединением множеств А и В называется множество, содержащее те и

Вычитание множеств Разностью множеств А и В называется множество, содержащее те и

Декартово произведение множеств Декартовым произведением множеств А и В называется множество всех

Изображение декартова произведения при помощи графа и таблицы А = {1, 2, 3}В = {3, 5}АВ1.2.3..3.5графтаблица

Изображение декартова произведения на координатной плоскости А = {1, 2, 3}В = {3, 5}

Слайды презентации

Слайд 2 МНОЖЕСТВО

ЭЛЕМЕНТ МНОЖЕСТВА

СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ

ПОДМНОЖЕСТВО

ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ

ОБЪЕДИНЕНИЕ МНОЖЕСТВ

ВЫЧИТАНИЕ МНОЖЕСТВ

ДЕКАРТОВО ПРОИЗВЕДЕНИЕ

МНОЖЕСТВ

выход

Слайд 3 Понятие множества — простейшее математическое понятие, оно не

Понятие множества — простейшее математическое понятие, оно не определяется, а лишь

определяется, а лишь поясняется при помощи примеров: множество книг

на полке, множество точек на прямой (точечное множество) и т. д.
Множества принято обозначать прописными буквами латинского алфавита: A, B, C… Z.

МНОЖЕСТВО

Множество дней недели,
Множество месяцев в году

Множество точек на прямой,
Множество натуральных чисел

Слайд 4 Элементы множества
Объекты, из которых образовано множество, называются

Элементы множества Объекты, из которых образовано множество, называются элементами.Элементы множества принято

элементами.
Элементы множества принято обозначать строчными буквами латинского алфавита: a,

b, c… z.
Если элемент х принадлежит множеству М, то записывают х О М, если не принадлежит – x П M

Если множество не содержит ни одного элемента, оно называется пустым и обозначается ∅ или 0.

Слайд 5 Способы задания множеств
А = {3, 4, 5,

Способы задания множеств А = {3, 4, 5, 6}Множество А двузначных

6}
Множество А двузначных чисел: свойство, которым обладает каждый элемент

данного множества, - «быть двузначным числом».

Слайд 6 Характеристическое свойство
Характеристическое свойство – это такое свойство,

Характеристическое свойство Характеристическое свойство – это такое свойство, которым обладает каждый

которым обладает каждый элемент, принадлежащий множеству, и не обладает

ни один элемент, который ему не принадлежит.

Этот способ задания множеств является общим и для конечных множеств, и для бесконечных.

«Множество А натуральных чисел, меньших 7»: А = {x | x ∈ N и x<7}

Слайд 7 подмножество
Множество В является подмножеством множества А (В

подмножество Множество В является подмножеством множества А (В ⊂ А), если

⊂ А), если каждый элемент множества В является также

элементом множества А. Пустое множество считают подмножеством любого множества. Любое множество является подмножеством самого себя.

Отношения между множествами наглядно представляют при помощи кругов Эйлера

Слайд 8 Круги Эйлера
Круги Эйлера – это особые чертежи,

Круги Эйлера Круги Эйлера – это особые чертежи, при помощи которых

при помощи которых наглядно представляют отношения между множествами.
Множества

А и В имеют общие элементы, но ни одно из них не является подмножеством другого

В М А

А М В

А = В

Множества А и В не пересекаются

А=В

Слайд 9 пересечение множеств
Пересечение множеств — множество, состоящее из

пересечение множеств Пересечение множеств — множество, состоящее из всех тех элементов,

всех тех элементов, которые принадлежат одновременно всем данным множествам.

Пересечение множеств А и В обозначают А∩В.

Если множества А и В не имеют общих элементов, то пишут: А З В = Ж

Характеристическое свойство формулируется путем соединения характеристических свойств пересекаемых множеств союзом «и». Например, если А – множество четных натуральных чисел, а В – двузначных чисел, то элементы их пересечения обладают свойством: «быть четными натуральными и двузначными числами»

А∩В

Слайд 10 Объединение множеств
Объединением множеств А и В называется

Объединение множеств Объединением множеств А и В называется множество, содержащее те

множество, содержащее те и только те элементы, которые принадлежат

множеству А или множеству В. Объединение множеств А и В обозначают А И В

Характеристическое свойство формулируется путем соединения характеристических свойств пересекаемых множеств союзом «или». Например, если А – множество четных натуральных чисел, а В – двузначных чисел, то элементы их объединения обладают свойством: «быть четными натуральными и двузначными числами»

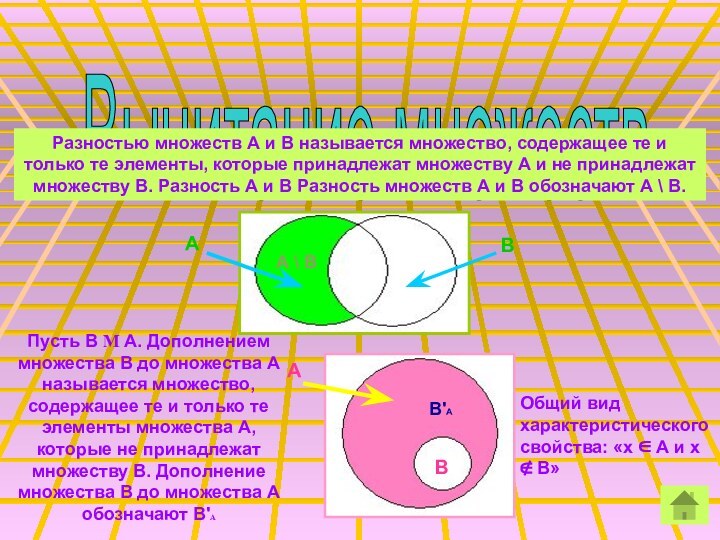
Слайд 11 Вычитание множеств
Разностью множеств А и В называется

Вычитание множеств Разностью множеств А и В называется множество, содержащее те

множество, содержащее те и только те элементы, которые принадлежат

множеству А и не принадлежат множеству В. Разность А и В Разность множеств А и В обозначают А \ В.

А \ В

Пусть В М А. Дополнением множества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принадлежат множеству В. Дополнение множества В до множества А обозначают В'А

В'А

Общий вид характеристического свойства: «x ∈ А и x ∉ В»

Слайд 12 Декартово произведение множеств
Декартовым произведением множеств А и

Декартово произведение множеств Декартовым произведением множеств А и В называется множество

В называется множество всех пар, первая компонента которых принадлежит

множеству А, а вторая компонента принадлежит множеству В. Декартово произведение обозначают А X В.

Операцию нахождения декартова произведения множеств называют декартовым умножением.

Если множества А и В конечны и содержат небольшое число элементов, можно изобразить декартово произведение этих множеств при помощи графа или таблицы.
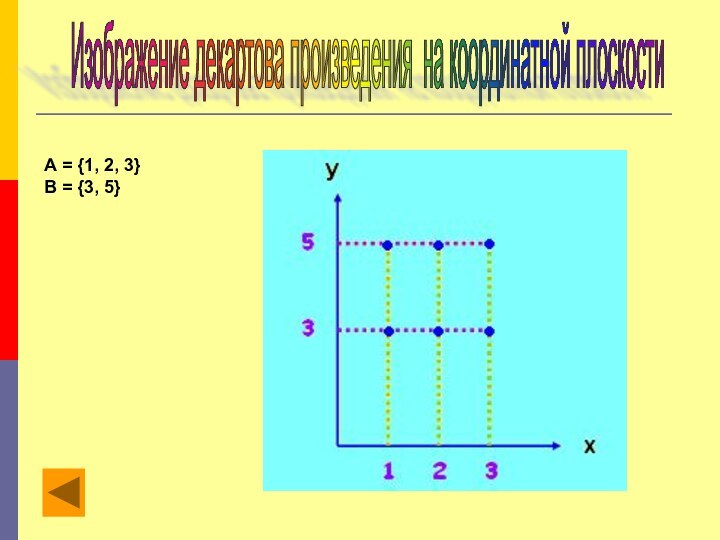
Декартово произведение двух числовых множеств (конечных и бесконечных) можно изображать на координатной плоскости.