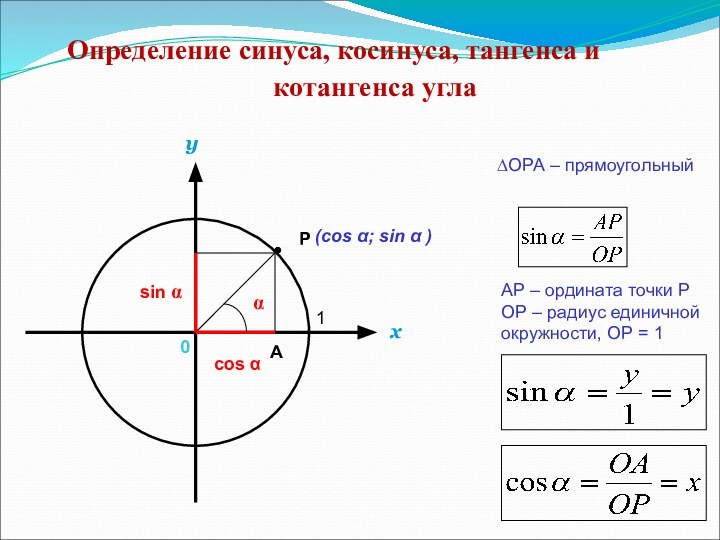
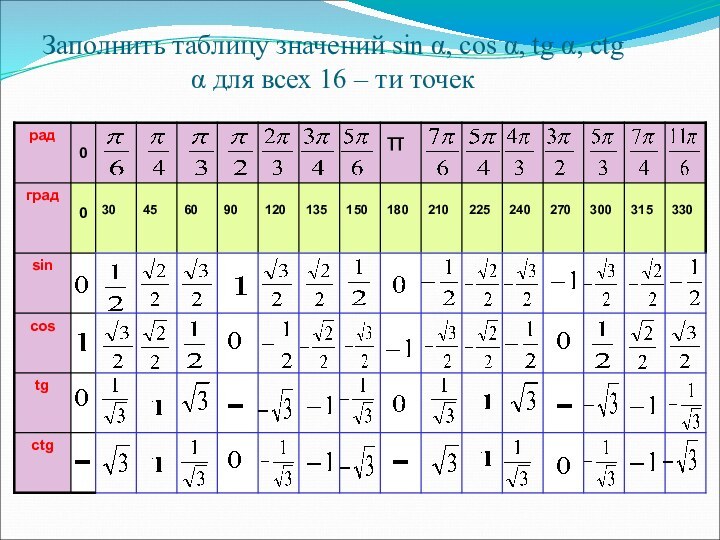
тангенса угла.
Уметь находить значения синуса, косинуса и тангенса по
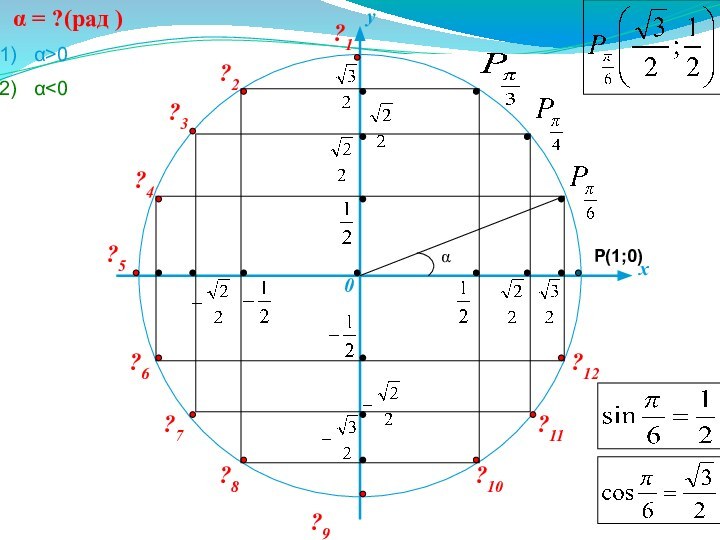
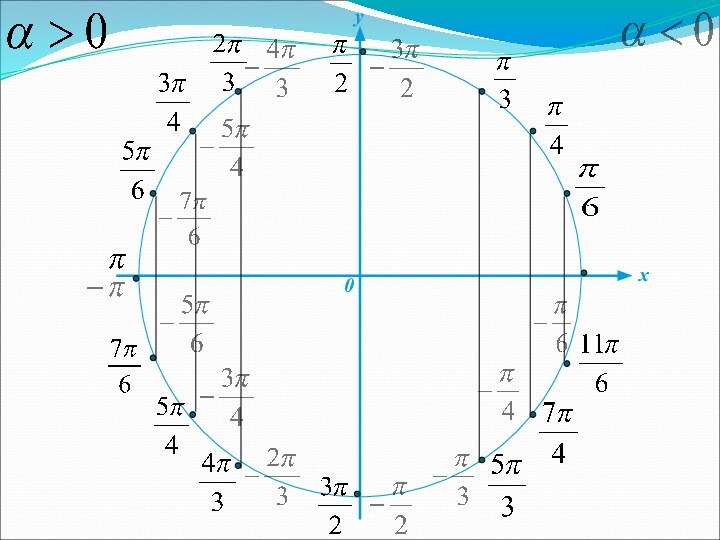
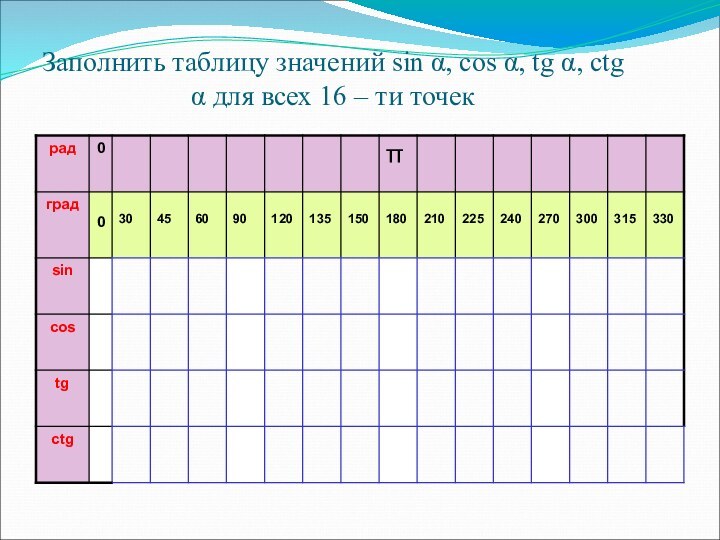
таблицам В.М. Брадиса, с помощью единичной окружности. Уметь решать уравнения:
sinx=0; sinx=1; sinx=-1;
cosx=0; cosx=1; cosx=-1.