и закрепить умения и навыки решения уравнений различными способами.
«Уравнение
- это золотой ключ, открывающий все матема- тические сезамы». Станислав Коваль
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


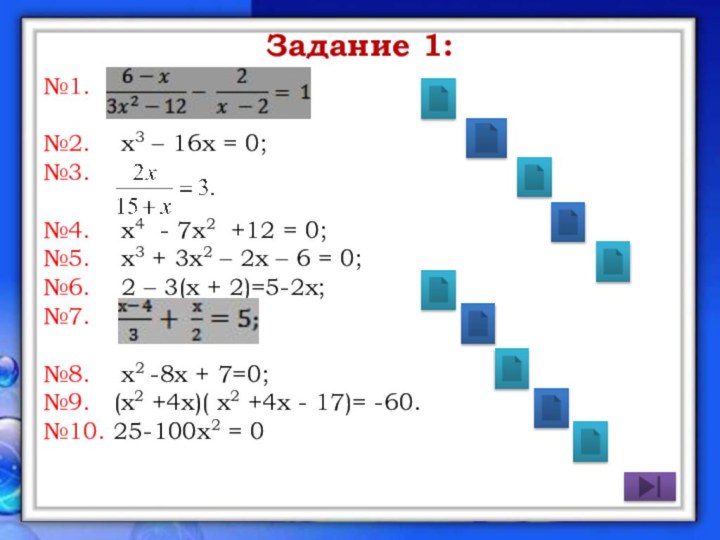



















х3 – 16х = 0
№3.
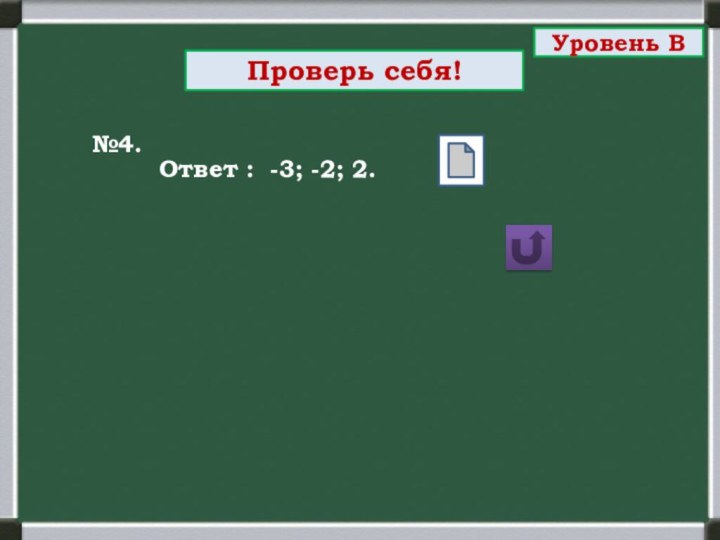
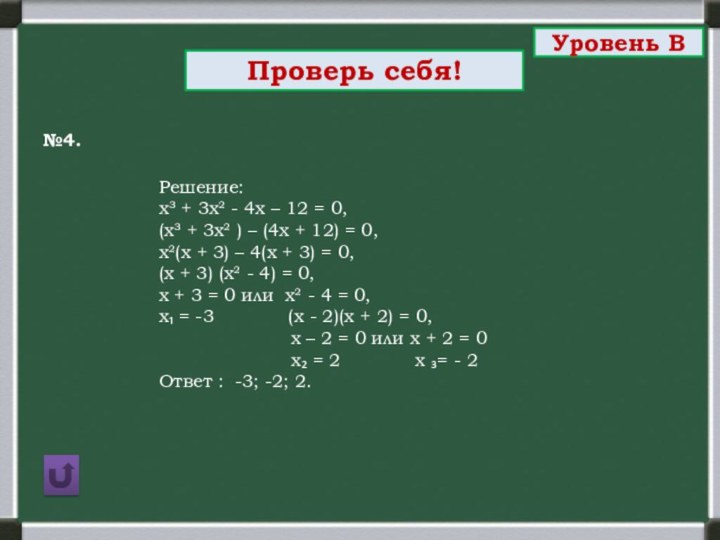
№4.
х4 - 7х2 +12 = 0
х2 - 8х + 7=0
№9. (х² + 4х)(х² + 4х - 17) = -60
25-100х2 = 0
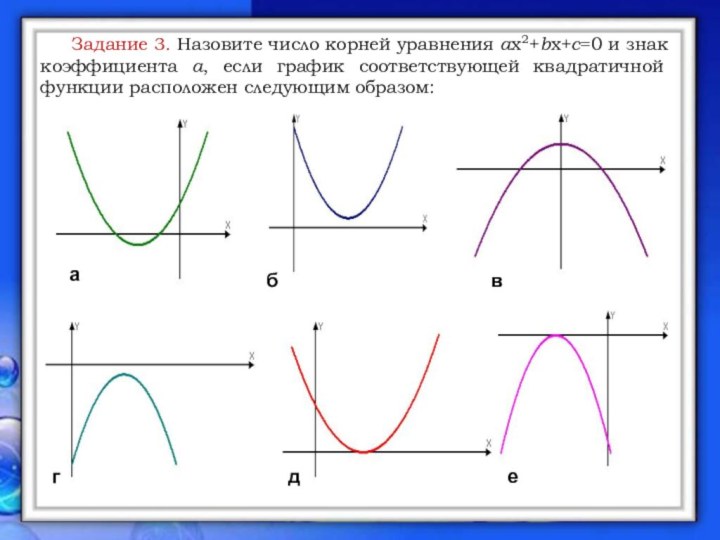
е
а
б
в
г
д
Рене Декарт
1596 - 1659
Электронный справочник
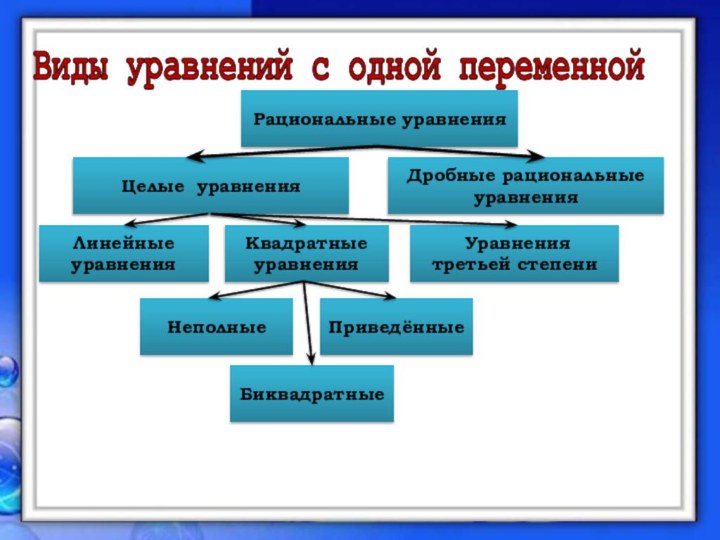
«Уравнения с одной переменной и способы их решений»
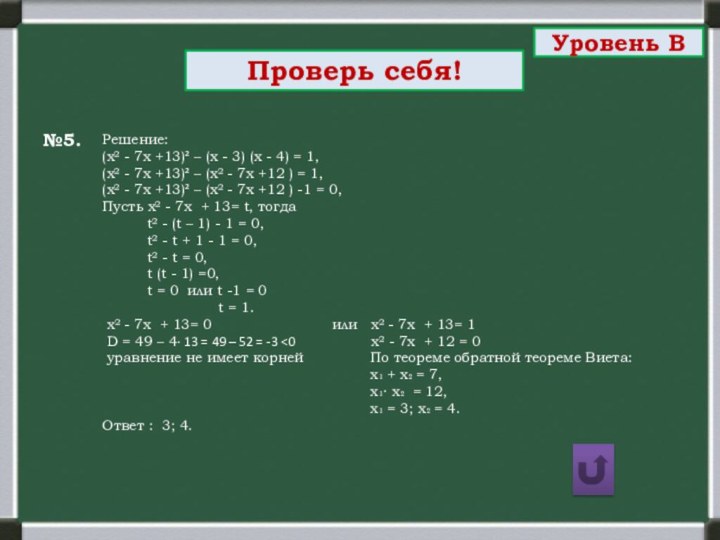
Проверь себя!
Проверь себя!
Проверь себя!
Проверь себя!
Уровень В
Проверь себя!
Проверь себя!
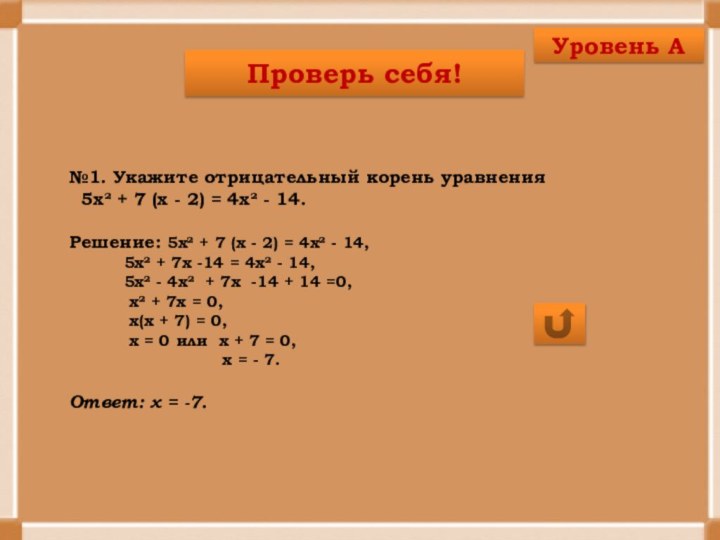
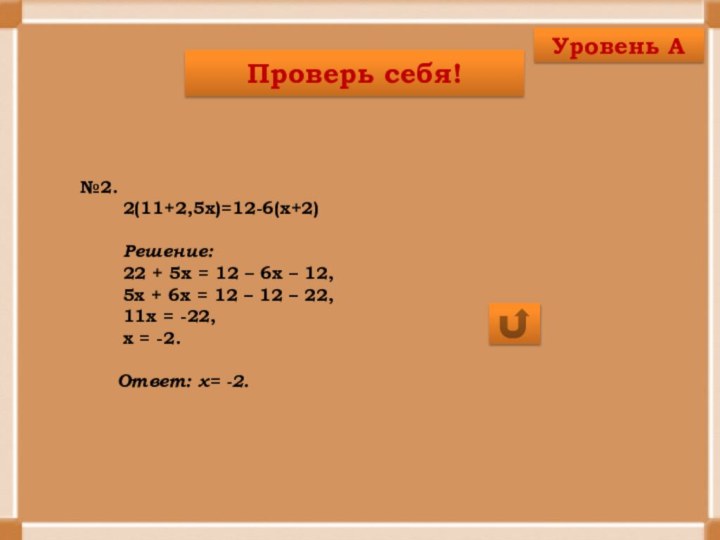
Уровень А
Проверь себя!
Уровень А
Проверь себя!
Уровень А
Уровень А
Уровень В
Уровень В