Слайд 2
Основные методы решения логических задач
метод рассуждений;
с помощью таблиц
истинности;
метод блок-схем;
средствами алгебры логики (алгебры высказываний);
графический (в том числе,
«дерево логических условий», метод кругов Эйлера);
метод математического бильярда;
метод последовательных рассуждений;
разновидность метода рассуждений — «с конца»;
табличный способ.
Слайд 3
Прием моделирования на полупрямой
Если в задаче имеется множество
объектов и требуется установить взаимоотношение между элементами этого множества,
то задачу можно решать на полупрямой.
Задача 1. На вечеринку собрались четверо друзей: Аня, Вика, Миша и Коля. Коля пришел раньше Ани, но не был первым. Определите, в какой последовательности друзья приходили к месту встречи, если Вика пришла последней.
Слайд 4
Решение
Решение. Построим модель описанной ситуации, считая обычный луч
«линией времени». Условимся пришедшего на вечеринку раньше обозначать на
полупрямой (первой буквой его имени) правее, пришедшего позже – левее. По порядку каждое условие отметим на полупрямой
а) Коля пришел раньше Ани:
б) Коля не был первым, то есть кто-то из друзей опередил Колю:
в) Вика пришла последней:
г) Значит, Миша пришел раньше всех:
Ответ: Миша, Коля, Аня, Вика.
Слайд 5
Задача 2. При взвешивании животных в зоопарке выяснилось,
что буйвол тяжелее льва, медведь легче буйвола, а рысь
легче льва. Выберите утверждения, которые верны при указанных условиях.
1) Рысь тяжелее буйвола.
2) Буйвол самый тяжелый из всех этих животных.
3) Медведь тяжелее буйвола.
4) Рысь легче буйвола.
Решение. Отметим данные задачи на полупрямой, причем с одной стороны полупрямой отметим однозначные данные, с другой стороны – неоднозначные.
Ответ: 24.
Слайд 6
Прием моделирования с помощью таблицы
Если в процессе решения
необходимо установить соответствие между элементами двух или нескольких различных
множеств, то целесообразно использовать таблицу.
Задача 3. Перед соревнованиями по плаванию каждого из четырех участников А, Б, В, Г спросили, на какое место он рассчитывает. А сказал: «Я буду первым», Б сказал: «Я не буду последним», В сказал: «Я не буду ни первым, ни последним» и Г сказал: «Я буду последним». После заплыва оказалось, что только один из них ошибочно предсказал результат. Кто из пловцов ошибся?
Слайд 7
Решение
Составим таблицу, в которой знаком «плюс» укажем предполагаемые
результаты.
Предположим, что ошибся А, тогда он мог занять 2-е
или 3-е место (4-е место занял пловец Г, который, если ошибся А, правильно предсказал свой результат, так как по условию ошибся только один пловец). В этом случае возможны следующие варианты распределения мест:
а) А – 2, Б – 1, В – 3, Г – 4;
б) А – 3, Б – 1, В – 2, Г – 4.
Слайд 8
Докажем, что действительно ошибся пловец А. Если бы
ошибся Б, т.е. занял 4-е место, то ошибся бы
и пловец Г, что противоречит условию задачи. Если бы ошибся В, тогда он должен быть или первым или последним. В таком случае ошибся бы еще один пловец – А или Г. Если бы ошибся Г, то ошибся бы еще один пловец, в противном случае последнее место не занял бы никто. Так как по условию задачи мог ошибиться только один пловец, то Г не ошибся.
Ответ: ошибся пловец А.
Слайд 9
Задача 4. После традиционного вечера встречи с выпускниками
школы в стенгазете появилась заметка о трех наших бывших
учениках. В ней было сказано, что Иван, Андрей и Борис стали учителями. Теперь они преподают разные дисциплины: один из них - математику, второй – физику, а третий – химию. Живут они тоже в разных городах: Минске, Витебске, Харькове. В заметке было также написано, что их первоначальные планы осуществились не полностью:
1) Иван живет не в Минске;
2) Андрей – не в Витебске;
3) житель Минска преподает не математику;
4) Андрей преподает не физику;
5) повезло только жителю Витебска: он преподает любимую им химию.
Можно ли по этим данным определить, кто где живет и что преподает?
Слайд 10
Решение
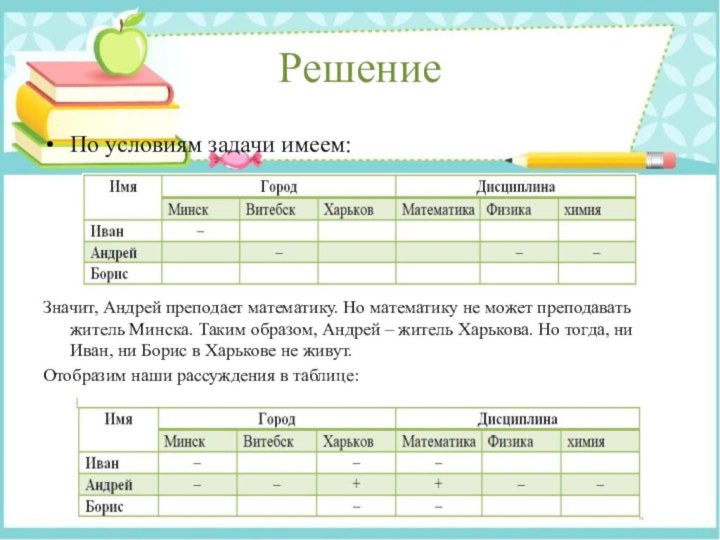
По условиям задачи имеем:
Значит, Андрей преподает математику. Но
математику не может преподавать житель Минска. Таким образом, Андрей
– житель Харькова. Но тогда, ни Иван, ни Борис в Харькове не живут.
Отобразим наши рассуждения в таблице:
Слайд 11
Из таблицы видно, что Иван не живет ни
в Минске, ни в Харькове. Следовательно, Иван – житель
Витебска и преподает химию:
Значит, Борис – житель Минска и преподает физику. Окончательно получим:
Ответ: Андрей преподает математику и живет в Харькове, Борис – физику и живет в Минске, Иван – химию и является жителем Витебска.
Слайд 12
Прием моделирования с помощью графов
Ситуации, в которых
требуется найти соответствие между элементами различных множеств, можно моделировать
с помощью графов. В этом случае элементы различных множеств будем обозначать точками (кружочками, прямоугольниками и т. п.), а соответствия между ними – отрезками (дугами).
Задача 5. Три товарища – Иван, Дмитрий и Степан преподают различные предметы (химию, биологию и физику) в школах Москвы, Тулы и Новгорода. О них известно следующее:
Слайд 13
Иван работает не в Москве, а Дмитрий –
не в Новгороде;
москвич преподает физику;
тот, кто работает в
Новгороде, преподает химию; Значит, Андрей преподает математику. Но математику не может преподавать житель Минска. Таким образом, Андрей – житель Харькова. Но тогда, ни Иван, ни Борис в Харькове не живут.
Слайд 14
Решение
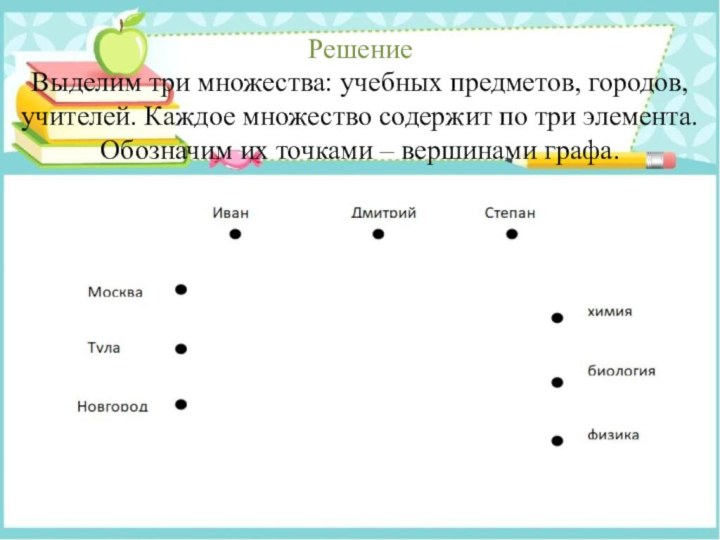
Выделим три множества: учебных предметов, городов, учителей. Каждое
множество содержит по три элемента. Обозначим их точками –
вершинами графа.
Слайд 15
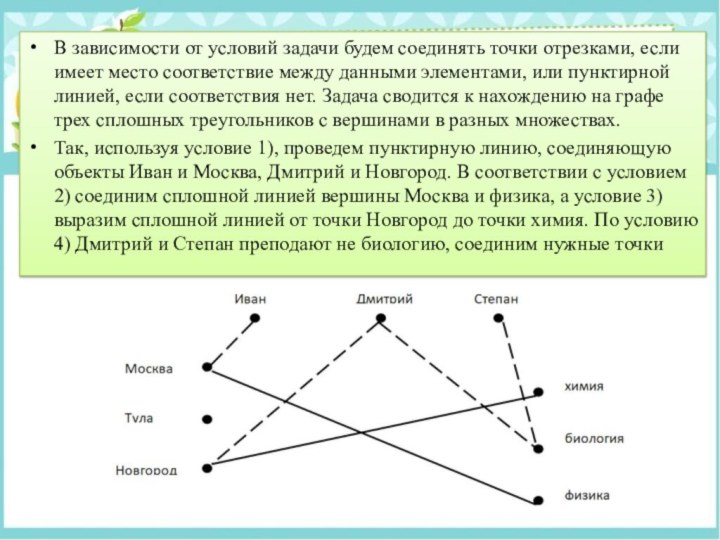
В зависимости от условий задачи будем соединять точки
отрезками, если имеет место соответствие между данными элементами, или
пунктирной линией, если соответствия нет. Задача сводится к нахождению на графе трех сплошных треугольников с вершинами в разных множествах.
Так, используя условие 1), проведем пунктирную линию, соединяющую объекты Иван и Москва, Дмитрий и Новгород. В соответствии с условием 2) соединим сплошной линией вершины Москва и физика, а условие 3) выразим сплошной линией от точки Новгород до точки химия. По условию 4) Дмитрий и Степан преподают не биологию, соединим нужные точки
Слайд 16
Получается, что биологию преподает Иван. Известно, что химик
живет в Новгороде, а физик – в Москве, значит,
биолог живет в Туле. Проведем соответствующие сплошные линии.
Слайд 17
Обратим внимание на треугольник, образованный вершинами Иван, Тула,
биология: в нем есть две сплошные стороны, значит, третью
сторону (Иван – Тула) также можно выделить сплошной линией. В самом деле, если Иван преподает биологию, а биолог живет в Туле, то Иван живет в Туле.
Слайд 18
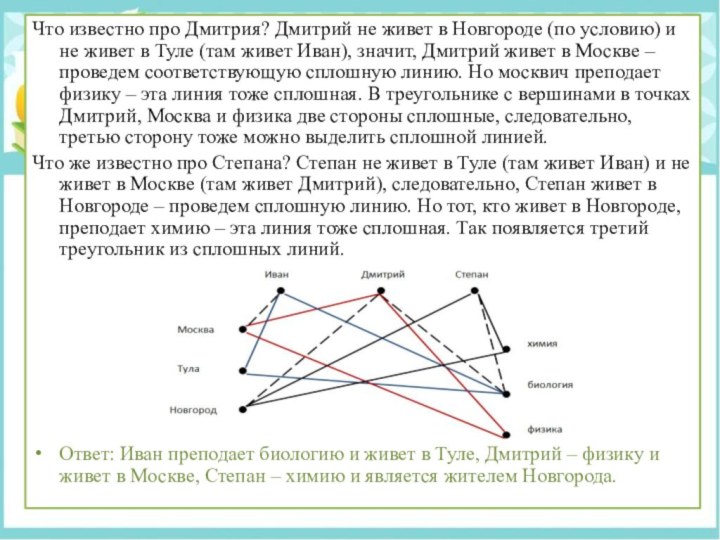
Что известно про Дмитрия? Дмитрий не живет в
Новгороде (по условию) и не живет в Туле (там
живет Иван), значит, Дмитрий живет в Москве – проведем соответствующую сплошную линию. Но москвич преподает физику – эта линия тоже сплошная. В треугольнике с вершинами в точках Дмитрий, Москва и физика две стороны сплошные, следовательно, третью сторону тоже можно выделить сплошной линией.
Что же известно про Степана? Степан не живет в Туле (там живет Иван) и не живет в Москве (там живет Дмитрий), следовательно, Степан живет в Новгороде – проведем сплошную линию. Но тот, кто живет в Новгороде, преподает химию – эта линия тоже сплошная. Так появляется третий треугольник из сплошных линий.
Ответ: Иван преподает биологию и живет в Туле, Дмитрий – физику и живет в Москве, Степан – химию и является жителем Новгорода.
Слайд 19
Прием моделирования с помощью диаграмм (кругов) Эйлера-Венна
Данный метод
позволяет графически решать математические задачи на основе применения теории
множеств.
Задача 6. В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический – 14, химический – 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек – и математический и физический, 5 – и математический и химический, 3 – и физический и химический.
Сколько учеников класса не посещают никаких кружков?
Слайд 20
Решение
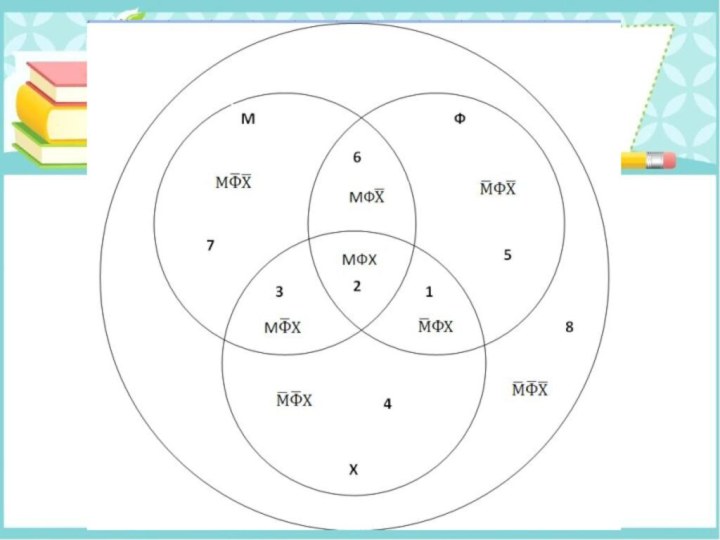
На рисунке самый большой круг изображает множество всех
учеников класса. Внутри этого круга расположены три пересекающихся круга
меньшего диаметра: эти круги изображают членов математического, физического и химического кружков и обозначены буквами М, Ф, Х.
Пусть МФХ – множество ребят, каждый из которых посещает все 3 кружка. Дадим аналогичные имена и другим множествам: МФ – множество занимающихся и в математическом, и в физическом кружке (и, возможно, также в химическом), МФ - и в математическом, и в физическом, но не в химическом и т.д.
Впишем нужные имена множеств в области, изображенные на рисунке:
Слайд 22
Обратимся к числовым данным. В область МФХ впишем

число 2, так как все три кружка посещают 2
ученика. Далее известно, что ребят, посещающих и математический, и физический кружок, - 8. Значит, множество МФ состоит из 8 человек. Но это множество является объединением множеств МФХ и МФ, причем в МФХ входят 2 человека. Значит, на долю МФ остается 6 человек.
Теперь рассмотрим множество МХ, состоящее из 5 человек. Оно также состоит из двух частей: на МФХ приходится 2 человека. Значит, на МХ – 3.
Множество ФХ состоит из 3 человек. На ФХ приходится 1 человек.
Рассмотрим теперь множество М, в которое входит 18 учеников. Оно состоит из четырех частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 3. Значит, в четвертое подмножество, а именно в М, входит 18 – (2 + 3 + 6) = 7 человек.
Аналогично определим количество учащихся в множествах и :
14 – (6 + 2 + 1) = 5, 10 – (3 + 2 + 1) = 4.
Три пересекающихся круга образуют 7 непересекающихся областей, изображающих непересекающиеся подмножества учеников, каждый из которых посещает хотя бы 1 кружок. Просуммируем цифры в этих областях: 6 + 5 + 7 + 3 + 2 + 1 + 4 = 28 человек посещает кружки.
Значит, 36 – 28 = 8 ребят не посещают никаких кружков.
Ответ: в классе 8 учеников, не посещающих кружки.
Слайд 23
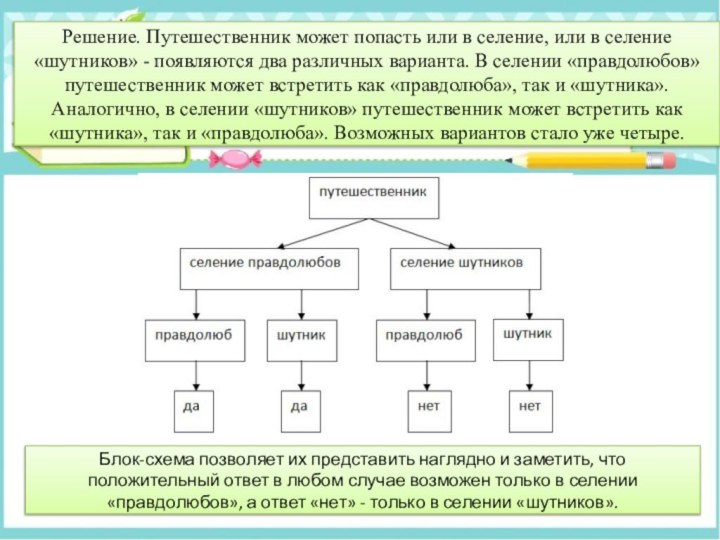
Прием моделирования с помощью блок-схемы
При применении данного метода
каждый шаг в рассуждении выделяется отдельным изображением (прямоугольником).
Задача 13.
На некотором острове отдельными селениями живут правдолюбы и шутники. Правдолюбы всегда говорят только правду, а шутники постоянно шутят, а поэтому всегда лгут. Жители одного племени бывают в селении другого, и наоборот. В одно из селений попал путешественник, но не знает, в какие именно. Доказать, что путешественнику достаточно первому встречному задать вопрос: «Вы местный?», чтобы по ответу определить, в селении какого племени он находится.