уравнения
Способы обнаружения постороннего корня
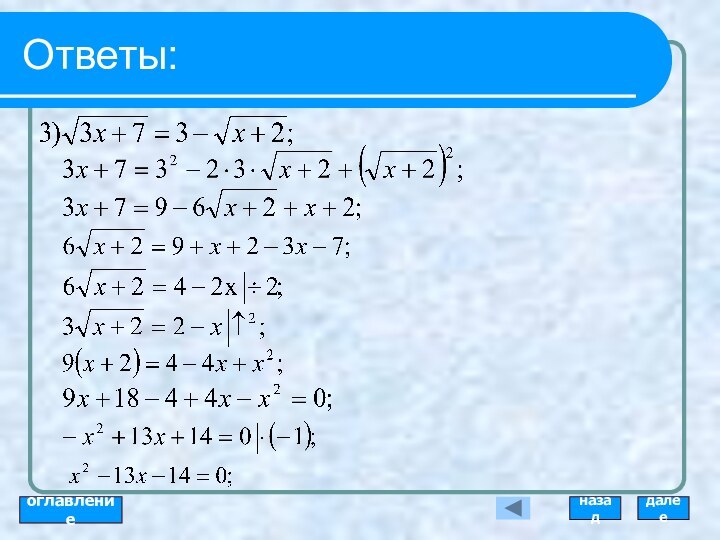
Алгоритм решения иррациональных уравнений
Метод подбора
(метод
пристального взгляда).Алгоритм решения методом подбора.
Определение равносильных уравнений.
Равносильные преобразования уравнений
Неравносильные преобразования уравнения
выход