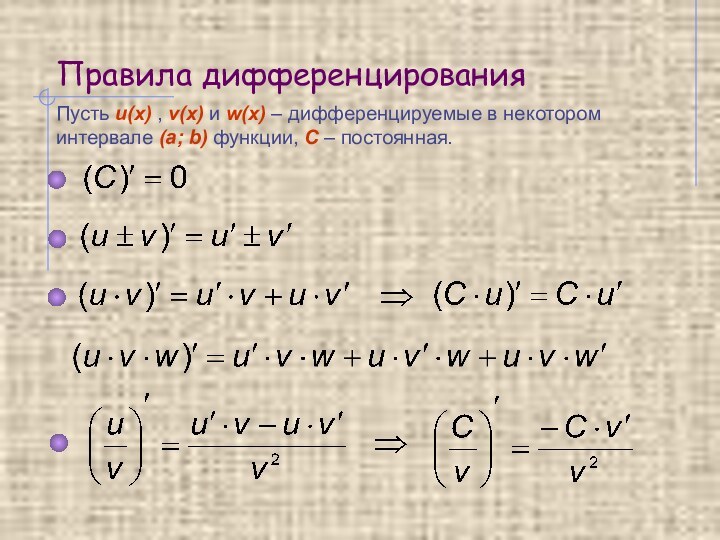Презентация на тему Определение производной

некотором интервале (a; b).
Аргументу x придадим некоторое приращение

х

f(x )

x+Δx

f(x+ Δx )

Найдем соответствующее приращение функции:

Если существует предел

то его называют производной функции y = f(x) и обозначают одним из символов:

имеющая производную в каждой точке интервала (a; b), называется

Значение производно функции y = f(x) в точке x0 обозначается одним из символов:

Если функция y = f(x) описывает какой – либо физический процесс, то f ’(x) есть скорость протекания этого процесса – физический смысл производной.

точки М и М1:

х

f(x )

x+Δx


М
М1

f(x+ Δx )

Через точки М

касательной к графику функции y = f(x) в точке,

Если точка касания М имеет координаты (x0; y0 ), угловой коэффициент касательной есть k = f ’(x0 ).

Уравнение прямой с угловым коэффициентом:

Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.

Уравнение касательной

Уравнение нормали

дифференцируема в некоторой точке , то она непрерывна в

Теорема

Пусть функция y = f(x) дифференцируема в некоторой точке х, следовательно существует предел:

Доказательство:

где

при

По теореме о связи функции, ее предела и бесконечно малой функции

Функция y = f(x) – непрерывна.

Обратное утверждение не верно: непрерывная функция может не иметь производной.

факториал

других основных элементарных функций.

дифференцируемые в некотором интервале (a; b) функции, С –

= φ(x) , тогда y = f(φ(x)) – сложная

Теорема

Это правило остается в силе, если промежуточных аргументов несколько:

= f(х) , разрешенным относительно y, то говорят, что

Для нахождения производной неявно заданной функции необходимо продифференцировать уравнение по х, рассматривая при этом y как функцию от х, и полученное выражение разрешить относительно производной.

Под неявным заданием функции понимают задание функции в виде уравнения не разрешенного относительно y:

заданную функцию сначала прологарифмировать, а затем результат продифференцировать.
Такую операцию