- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Повторение и расширение понятия функции (9 класс)
Содержание
- 2. Определение функции. Обозначение функции.
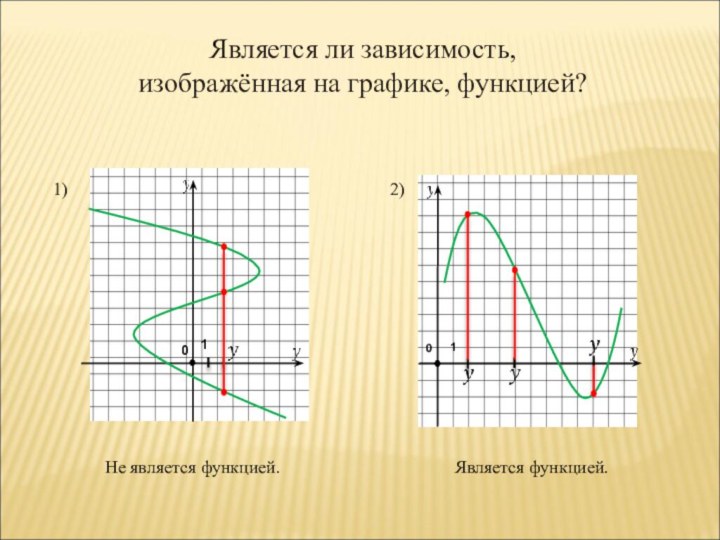
- 3. Является ли зависимость,изображённая на графике, функцией?0 0 11)2) Не является функцией. Является функцией.1
- 4. Способы задания функции. ОписательноС помощью формулыС помощью таблицыграфически
- 5. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ. Область определения функции
- 6. ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ. Область значений функции
- 7. 1. УКАЖИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ, КОТОРАЯ ЗАДАНА ТАБЛИЦЕЙ:
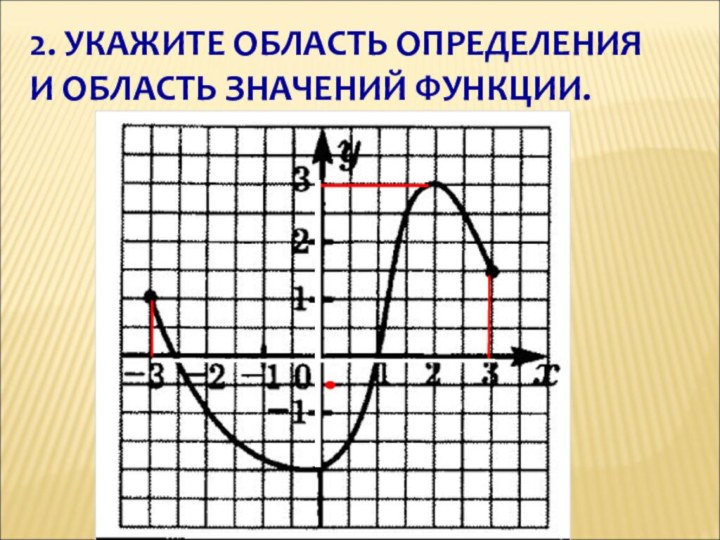
- 8. 2. УКАЖИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ.
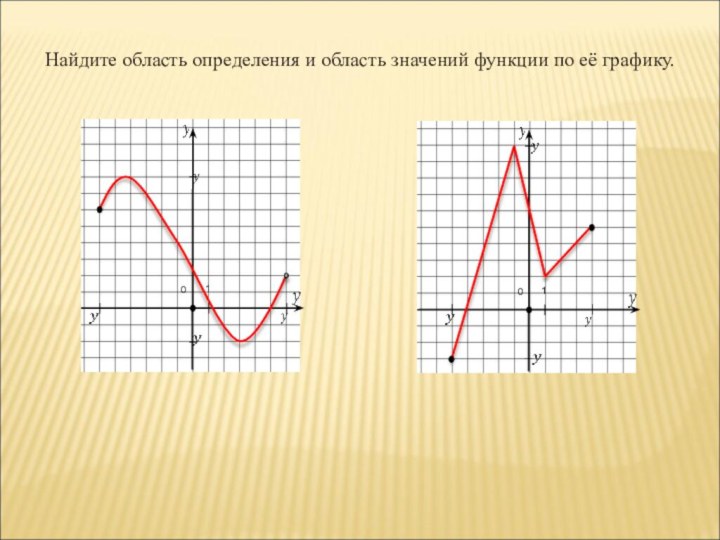
- 9. Найдите область определения и область значений функции по её графику.0 1 0 1
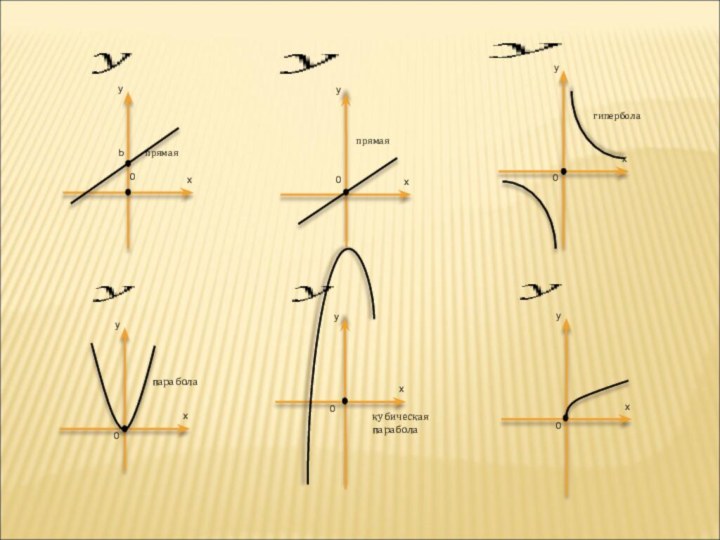
- 10. ГРАФИК ФУНКЦИИ
- 11. кубическаяпарабола
- 12. f(-3) = f(- 1) = f(x) =
- 13. Найдите значение функции при заданномзначении аргумента.
- 14. 1. Область определения2. Область значений3. Нули функции4.
- 15. Нулем функции y = f (x) называется
- 16. ЧетностьЧетная функцияНечетная функцияФункция y = f(x) называется
- 17. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВАПромежутки, на которых непрерывная функция
- 18. НЕПРЕРЫВНОСТЬ Функция называется непрерывной на промежутке, если
- 19. МОНОТОННОСТЬ Функцию у = f(х) называют
- 20. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯЧисло m называют наименьшим
- 22. ОГРАНИЧЕННОСТЬФункцию у = f(х) называют ограниченной снизу
- 23. ВЫПУКЛОСТЬ Функция выпукла вниз на промежутке Х
- 24. РАБОТА С УЧЕБНИКОМ
- 25. Скачать презентацию
- 26. Похожие презентации













Слайд 5
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ.
Область определения функции у(х)
это
все значения аргумента - Х
Обозначение
области
определения - D(у)
Слайд 6
ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ.
Область значений функции у(х)
это
все значения - У _
Обозначение области значений - Е(у)
Слайд 12
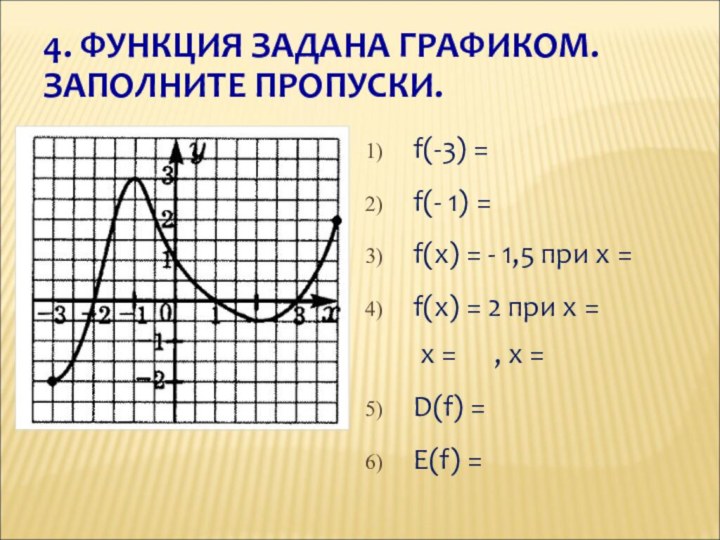
f(-3) =
f(- 1) =
f(x) = -
1,5 при x =
f(x) = 2 при х
=
х = , x = D(f) =
E(f) =
4. ФУНКЦИЯ ЗАДАНА ГРАФИКОМ. ЗАПОЛНИТЕ ПРОПУСКИ.
Слайд 14
1. Область определения
2. Область значений
3. Нули функции
4. Четность
5.
Промежутки знакопостоянства
6. Непрерывность
7. Монотонность
8. Наибольшее и наименьшее значения
9. Ограниченность
10.
ВыпуклостьСВОЙСТВА ФУНКЦИИ
Алгоритм описания свойств функции
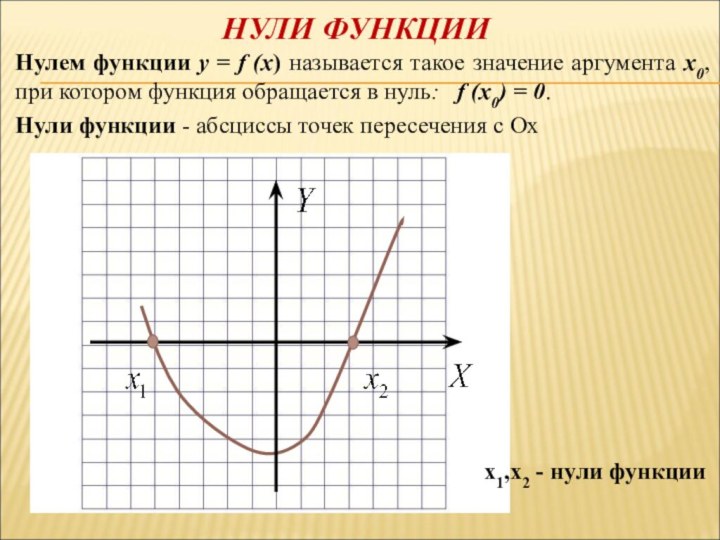
Слайд 15 Нулем функции y = f (x) называется такое
значение аргумента x0, при котором функция обращается в нуль:
f (x0) = 0.Нули функции - абсциссы точек пересечения с Ох
НУЛИ ФУНКЦИИ
x1,x2 - нули функции
Слайд 16
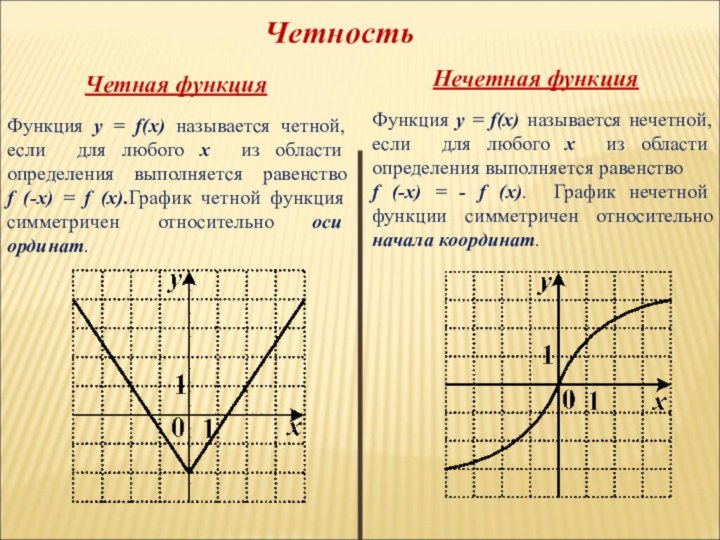
Четность
Четная функция
Нечетная функция
Функция y = f(x) называется четной,
если для любого х из области определения выполняется равенство
f (-x) = f (x).График четной функция симметричен относительно оси ординат.Функция y = f(x) называется нечетной, если для любого х из области определения выполняется равенство
f (-x) = - f (x). График нечетной функции симметричен относительно начала координат.
Слайд 17
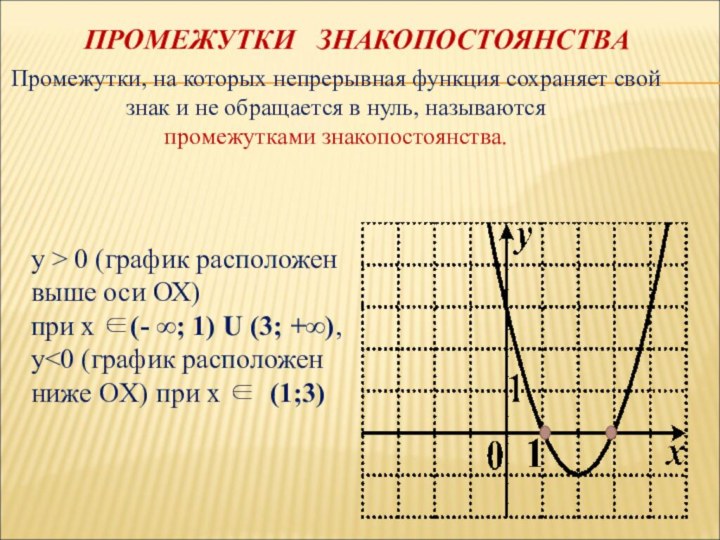
ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА
Промежутки, на которых непрерывная функция сохраняет
свой знак и не обращается в нуль, называются
промежутками
знакопостоянства.y > 0 (график расположен выше оси ОХ)
при х ∈(- ∞; 1) U (3; +∞),
y<0 (график расположен ниже OX) при х ∈ (1;3)
Слайд 18
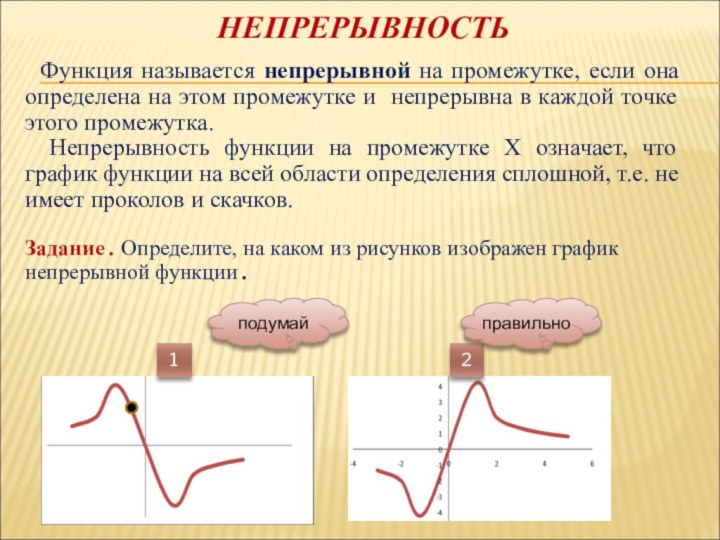
НЕПРЕРЫВНОСТЬ
Функция называется непрерывной на промежутке, если она
определена на этом промежутке и непрерывна в каждой точке
этого промежутка.Непрерывность функции на промежутке Х означает, что график функции на всей области определения сплошной, т.е. не имеет проколов и скачков.
Задание . Определите, на каком из рисунков изображен график непрерывной функции .
1
2
подумай
правильно
Слайд 19
МОНОТОННОСТЬ
Функцию у = f(х) называют
возрастающей на множестве Х, если для любых двух
точек х1 и х2 из области определения, таких, что х1 < х2, выполняется неравенствоf(х1) < f(х2) .
Функцию у = f(х) называют убывающей на множестве Х, если для любых двух точек
х1 и х2 из области определения, таких, что х1 < х2, выполняется неравенство
f(х1) >f(х2) .
x1
х1
x2
f(x2)
f(x1)
x2
x1
x2
f(x2)
f(x1)
Слайд 20
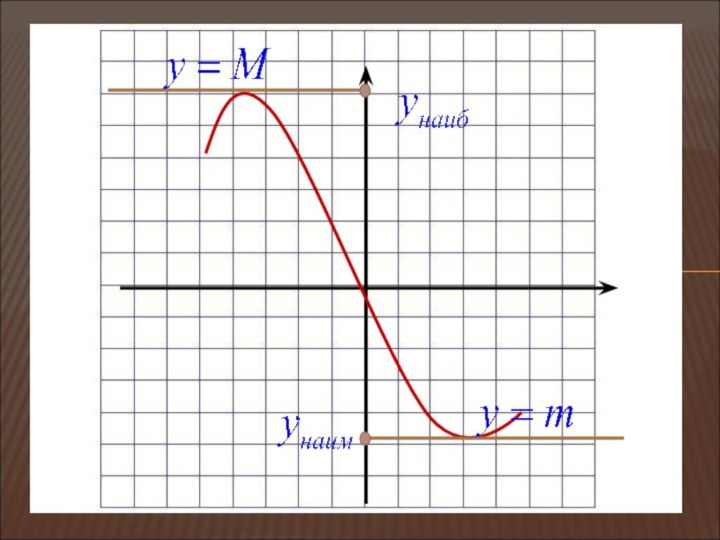
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
Число m называют наименьшим значением
функции
у = f(х) на множестве Х, если:
1) в области определения существует такая точка х0, что f(х0) = m.
2) всех х из области определения выполняется неравенство
f(х) ≥ f(х0).
Число M называют наибольшим значением функции
у = f(х) на множестве Х, если:
1) в области определения существует такая точка х0, что f(х0) = M.
2) для всех х из области определения выполняется неравенство
f(х) ≤ f(х0).
Слайд 22
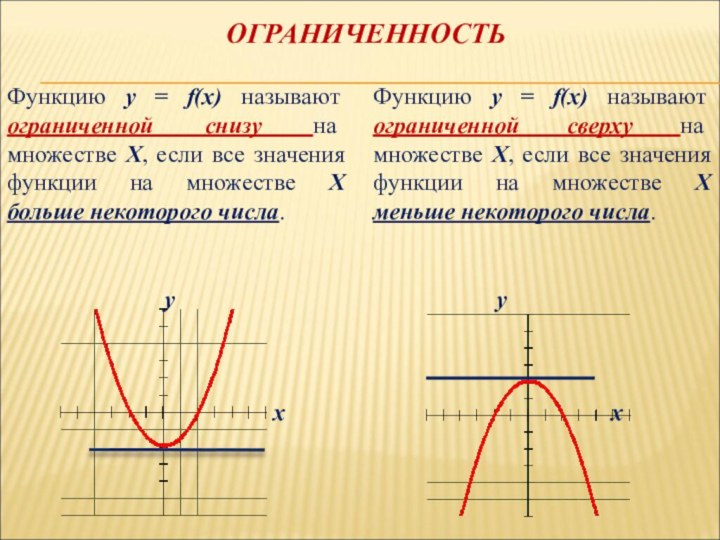
ОГРАНИЧЕННОСТЬ
Функцию у = f(х) называют ограниченной снизу на
множестве Х, если все значения функции на множестве Х
больше некоторого числа.Функцию у = f(х) называют ограниченной сверху на множестве Х, если все значения функции на множестве Х меньше некоторого числа.
х
у
х
у
Слайд 23
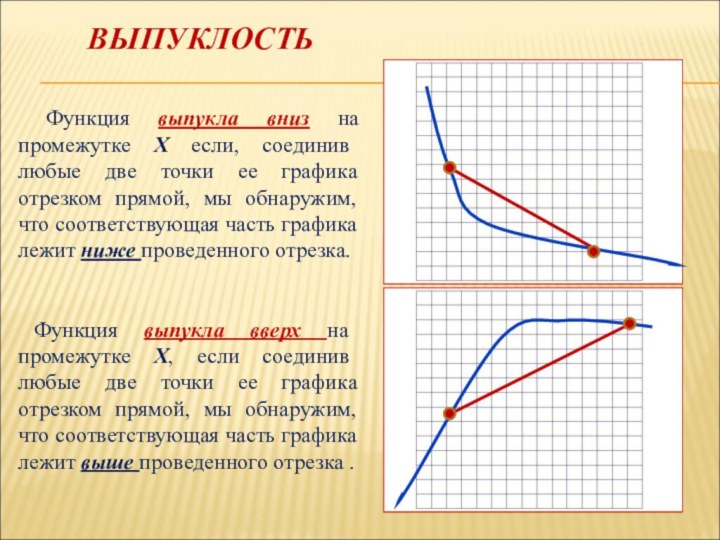
ВЫПУКЛОСТЬ
Функция выпукла вниз на промежутке Х если,
соединив любые две точки ее графика отрезком прямой, мы
обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.Функция выпукла вверх на промежутке Х, если соединив любые две точки ее графика отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка .





























