Презентация на тему по теме: Квадратные уравнения

не любит математику, не верь.
Её

нельзя не любить - её можно только не знать.

где х –переменная,

а, в и с

некоторые числа,

причем а 0.

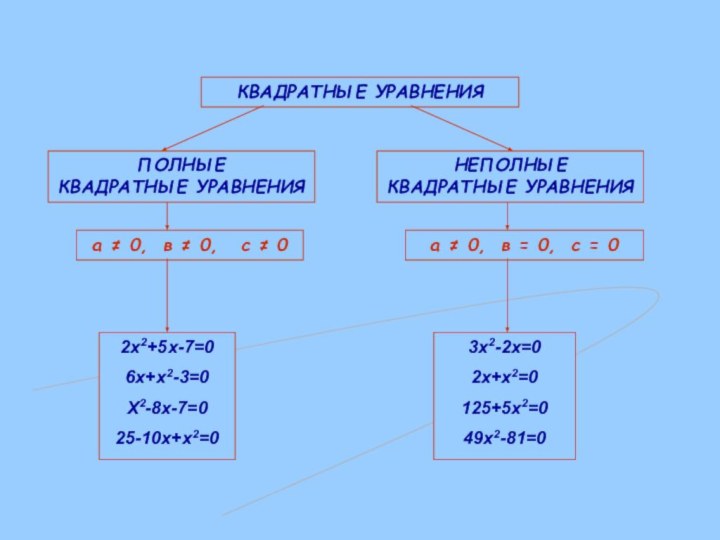
ОПРЕДЕЛЕНИЕ:

Квадратным уравнением называется

0, с ≠ 0
а ≠ 0, в =

0, с = 0

2х2+5х-7=0
6х+х2-3=0
Х2-8х-7=0
25-10х+х2=0

3х2-2х=0
2х+х2=0
125+5х2=0
49х2-81=0

12х - х2 + 7 = 0
в) 8 +

5х2 = 0
г) х – 6х2 = 0
д) - х + х2 = 15

а = 6, в = -1, с = 4;
а = -1, в = 12, с = 7;
а = 5, в = 0, с = 8;
а = -6, в =1, с = 0;
а = 1, в =-1, с = -15.

Определите коэффициенты
квадратного уравнения:

правую часть уравнения.
ах2= -с
2.Деление обеих частей уравнения на а.
х2=

-с/а
3.Если –с/а>0 -два решения:
х1 = и х2 = -

Если –с/а<0 - нет решений

Вынесение х за скобки:
х(ах + в) = 0
2. Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а

1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.

б) ( х + 2)2 + ( х -3)2 = 13

2 вариант:
а) 2х + х2= 0
б) 49х2 – 81 = 0

3 вариант:
а) 3х2 – 2х = 0
б) 125 + 5х2 = 0

= b2- 4ac, x1,2=

График.

Теорема Виета.

- х + 3х2 – 70 =0

2 вариант: 2х2 -9х + 10 = 0

3 вариант: х2 – 8х -9 = 0

а) -7х + 5х2 + 1 =0

б) (х – 1)(х + 1) = 2 (5х – 10,5)

2 вариант: а) 2х2 + 5х -7 = 0
б) –х2 = 5х - 14

3 вариант: а) х2 – 8х + 7 = 0
б) 6х – 9 = х2

-х = - 2/3

2 вариант: а) х2 + 1,5х = 2,5

3 вариант: а) 6х + х2– 3 =0

математика и астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в)

изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму.
________________________________________________
Вот задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?