- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Предел
Содержание
- 2. ОГЛАВЛЕНИЕТитульная страницаОглавлениеВступлениеПредел переменной величиныОсновные свойства пределовПредел функции в точкеПонятие о непрерывности функцииПредел функции на бесконечностиЗамечательные пределыЗаключение
- 3. ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫПредел – одно из основных
- 4. 1. ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫПусть переменная величина x
- 5. 2. ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ 1. Предел алгебраической суммы
- 6. 3.ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ Определение 2. Число
- 7. 4. ПОНЯТИЕ О НЕПРЕРЫВНОСТИ ФУНКЦИИ 2. ВычислитьРешение.
- 8. 5. ПРЕДЕЛ ФУНКЦИИ НА БЕСКОНЕЧНОСТИ3.Найти Решение. При
- 9. 6. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ Некоторые пределы невозможно найти
- 10. 7. ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ 1.
- 11. Скачать презентацию
- 12. Похожие презентации
ОГЛАВЛЕНИЕТитульная страницаОглавлениеВступлениеПредел переменной величиныОсновные свойства пределовПредел функции в точкеПонятие о непрерывности функцииПредел функции на бесконечностиЗамечательные пределыЗаключение










Слайд 2
ОГЛАВЛЕНИЕ
Титульная страница
Оглавление
Вступление
Предел переменной величины
Основные свойства пределов
Предел функции в
точке
Слайд 3
ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ
Предел – одно из основных понятий
математического анализа. Понятие предела использовалось еще Ньютоном во второй
половине XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела дали Больцано в 1816 году и Коши в 1821 году.
Слайд 4
1. ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ
Пусть переменная величина x в
процессе своего изменения неограниченно приближается к числу 5, принимая
при этом следующие значения: 4,9; 4,99;4,999;…или 5,1; 5,01; 5,001;… В этих случаях модуль разности стремится к нулю: = 0,1; 0,01; 0,001;…Число 5 в приведенном примере называют пределом переменной величины x и пишут lim x = 5.
Определение 1. Постоянная величина a называется пределом переменной x, если модуль разности при изменении x становится и остается меньше любого как угодно малого положительного числа e.
Слайд 5
2. ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ
1. Предел алгебраической суммы конченного
числа переменных величин равен алгебраической сумме пределов слагаемых:
lim(x +
y + … + t) = lim x + lim y + … + lim t.2. Предел произведения конечного числа переменных величин равен произведению их пределов:
lim(x·y…t) = lim x · lim y…lim t.
3. Постоянный множитель можно выносить за знак предела:
lim(cx) = lim c · lim x = c lim x.
Например, lim(5x + 3) = lim 5x + lim 3 = 5 lim x + 3.
4. Предел отношения двух переменных величин равен отношению пределов, если предел знаменателя не равен нулю:
lim = lim y
5. Предел целой положительной степени переменной величины равен той же степени предела этой же переменной:
lim = (lim x)n
Например: = = x3 + 3 x2 = (-2)2 + 3·(-2)2 = -8 + 12 = 4
6. Если переменные x, y, z удовлетворяют неравенствам x и x z y
Слайд 6
3.ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
Определение 2. Число b называется
пределом* функции в точке a, если
для всех значений x, достаточно близких к a и отличных от a, значения функции сколь угодно мало отличаются от числа b.1.Найти: (3x2 – 2x).
Решение. Используя последовательно свойства 1,3 и 5 предела, получим
(3x2 – 2x) = (3x2) - (2x) = 3 x2 - 2 x = 3 - 2 x = 3 22 - 2·2 = 8
Слайд 7
4. ПОНЯТИЕ О НЕПРЕРЫВНОСТИ ФУНКЦИИ
2. Вычислить
Решение. При x
= 1 дробь
определена, так как ее знаменатель отличен от нуля. Поэтому для вычисления предела достаточно заменить аргумент его предельным значением. Тогда получимУказанное правило вычисления пределов нельзя применять в следующих случаях:
1)Если функция при x = a не определена;
2)Если знаменатель дроби при подстановке x = a оказывается равным нулю;
3)Если числитель и знаменатель дроби при подстановке x = a одновременно оказывается равным нулю или бесконечности.
В таких случаях пределы функций находят с помощью различных искусственных приемов.
Слайд 8
5. ПРЕДЕЛ ФУНКЦИИ НА БЕСКОНЕЧНОСТИ
3.Найти
Решение. При x
знаменатель х + 5 также стремится к
бесконечности, а обратная ему величина 0. Следовательно, произведение · 3 = стремится к нулю, если x . Итак, = 0
Слайд 9
6. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ
Некоторые пределы невозможно найти теми способами,
которые были изложены выше. Пусть например, требуется найти
. Непосредственная подстановка вместо аргумента его предела дает неопределенность вида 0/0. Невозможно также преобразовать числитель и знаменатель таким образом, чтобы выделить общий множитель, предел которого равен нулю.Поступим следующим образом. Возьмем круг с радиусом, равным 1, и построим центральный угол АОВ, равный 2х радианам. Проведем хорду АВ и касательные АD и ВD к окружности в точках А и В. Очевидно, что |AC| = |CB| = sin x, |AD| = |DB| = tg х
= 1 – Первый замечательный предел.
x = e 2,7182…,.
x – Второй замечательный предел.
Решение. Разделив числитель и знаменатель на x,получим
x = ( )x = = =
Слайд 10
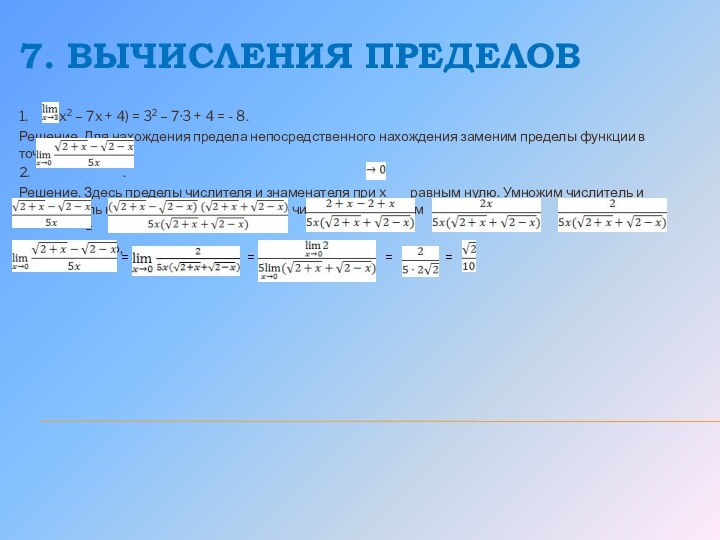
7. ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
1. (x2
– 7x + 4) = 32 – 7·3 +
4 = - 8.Решение. Для нахождения предела непосредственного нахождения заменим пределы функции в точке.
2. .
Решение. Здесь пределы числителя и знаменателя при x равным нулю. Умножим числитель и знаменатель на выражение ,сопряженное числителю, получим
= = = =
Следовательно,
=
=
=
=





























