Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Методическая разработка открытого урока на тему: Тригонометрия

Содержание

Тема урока: Решение простейших тригонометрических уравнений
ГБПОУ АЭК Преподаватель математикиСултаханова З.Р.Хасавюрт-2018г урок № 32-33 Тема урока: Решение простейших тригонометрических уравнений Цели урока:Образовательные: обобщить знания по теме « Тождественные преобразовании План урока:Применение тригонометрии в жизни«Счастливый случай» - актуализация знаний3. Решение простейших Тригонометрия в астрономии 2. sin a позволяет измерить расстояние, когда точное измерение Тригонометрия? Геометрия?Тригонометрия раздел математики, изучающий соотношение сторон и углов в треугольнике.Что Практическое применение тригонометрии Применение в техникеПрименения тригонометрии разнообразны. Принцип действия самозахватывающего ключа основан на измерении Применение в электротехникеВ технике и окружающем нас мире часто приходится сталкиваться с 1курсГБПОУАЭК I гейм«Дальше, дальше, дальше …»II гейм«Заморочки из бочки»IV гейм«Темная лошадка»III гейм«Ты - мне, я - тебе» I гейм«Дальше, дальше, дальше …» Найти значение выраженияопределение1 Найти значение выраженияопределение1 Найти значение выраженияопределение2 Найти значение выраженияопределение2 Определить знак выражениясвойства тригонометрических функций3 Определить знак выражениясвойства тригонометрических функций3 Найдите градусную меру угла4радианная мера угла Найдите градусную меру угла4радианная мера угла II гейм«Заморочки из бочки» 10876 Счастливый случай592413 В прямоугольном треугольнике отношение противолежащего катета к гипотенузе называетсясинусом острого угла. Отношение прилежащего катета к гипотенузе - косинусом острого угла. В каких четвертях cos α>0? 1 и 4 В какой четверти находится угол, равный 371° ? 1 Вычислите:2arccos 0+3 arccos1 Вычислите: 12arcsin0+ 3arccos -3 Может ли существовать такой треугольник, у которого углы  30º,П/4; 2П/3? Нет, так Может ли косинус или синус быть равным:0,75 Упростите выражение: Мяч бросили под уклоном ɑ к плоской горизонтальной поверхности земли. Время + 3 очка Сравните:2arcsin(cos45º) и Ты - мне , я - тебе IV гейм«Темная лошадка» Решение простейших тригонометрических уравненийТема урока: Ситуационная задача: Ваше рыболовецкое судно попало в шторм. Капитан принял Обозначим хч - время, через которое произойдёт встреча. Тогда АС - первоначальное .Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим. Примеры.Что называется Формулы корней простейших тригонометрических уравнений1.cost = а , где |а| ≤ 1илиЧастные Формулы корней простейших тригонометрических уравнений2. sint = а, где | а Формулы корней простейших тригонометрических уравнений3. tgt = а, аЄR t = arctg Рассмотрим частные случаи нашего уравнения cos x = a cos x = 1 cos x = 0  cos x Решение уравнений: Решение уравнений: Решение уравнений: Решение какого уравнения показано на тригонометрической окружности?sin x = 1/2 1. Решение какого уравнения показано на тригонометрической окружности?cos x = √2/2 2. 2) уметь определять значения синуса, косинуса, тангенса и котангенса для точек числовой Рефлексия Чем мы с вами занимались на уроке? Что нового вы узнали? Не забывайте готовиться к урокам!Обратные тригонометрические функции. Арксинус, арккосинус, арктангенс.План урока:Уравнения Виды тригонометрических уравнений1.Сводимые к квадратным Решаются методом введения новой переменной a∙sin²x Однородные тригонометрические уравненияУравнение вида asinx + bcosx = 0 2.Однородные1)Первой степени: Решаются делением на cos х (или sinx) и методом введения
Слайды презентации

Слайд 2 Тема урока:
Решение простейших
тригонометрических
уравнений

Тема урока: Решение простейших тригонометрических уравнений

Слайд 3 Цели урока:
Образовательные: обобщить знания по теме

Цели урока:Образовательные: обобщить знания по теме « Тождественные преобразовании

« Тождественные преобразовании в тригонометрии», сформировать навыки и

умения по решению простейших тригонометрических уравнений, научить применять знания, умения и навыки в новой ситуации
2. Развивающие: развивать логическое мышление,
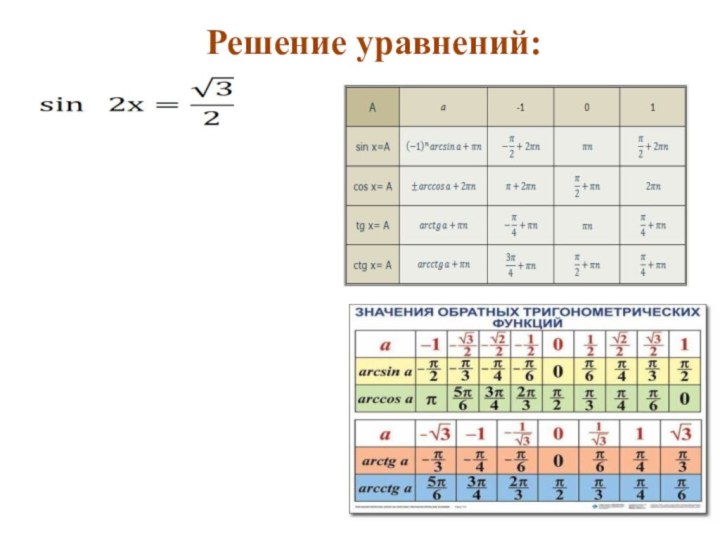
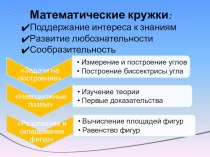
вычислительные навыки, умение пользоваться опорными конспектами, таблицами, расширить кругозор учащихся,
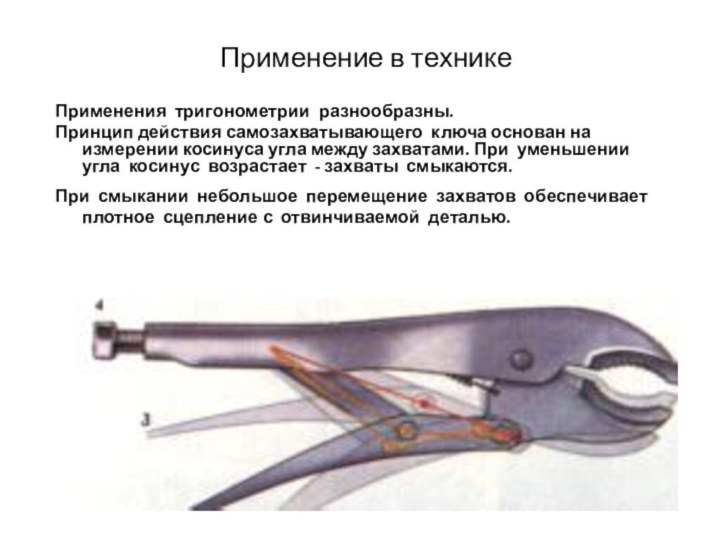
3. Воспитательные: воспитывать стремление к овладению знаниями, интерес к предмету, культуру мышления, культуру речи, познакомить учащихся с практическим применением тригонометрии в различных областях деятельности человека

Слайд 4 План урока:
Применение тригонометрии в жизни
«Счастливый случай» - актуализация

План урока:Применение тригонометрии в жизни«Счастливый случай» - актуализация знаний3. Решение простейших

знаний
3. Решение простейших тригонометрических уравнений
4. Опережающее

домашнее задание

Слайд 5 Тригонометрия в астрономии

2. sin a позволяет измерить

Тригонометрия в астрономии 2. sin a позволяет измерить расстояние, когда точное

расстояние,
когда точное измерение провести
невозможно.
2
1
30º
sin30º = ½
1. Сила

тригонометрии в том , что
она выступает как словарь переводящий
геометрию на язык чисел и наоборот.

Слайд 6 Тригонометрия? Геометрия?
Тригонометрия
раздел математики, изучающий
соотношение сторон

Тригонометрия? Геометрия?Тригонометрия раздел математики, изучающий соотношение сторон и углов в


и углов в треугольнике.

Что означает соотношение
сторон и углов в

треугольнике?

Слайд 7

Слайд 8 Практическое применение
тригонометрии

Практическое применение тригонометрии

Слайд 9 Применение в технике
Применения тригонометрии разнообразны.
Принцип действия самозахватывающего

Применение в техникеПрименения тригонометрии разнообразны. Принцип действия самозахватывающего ключа основан на

ключа основан на измерении косинуса угла между захватами. При

уменьшении угла косинус возрастает - захваты смыкаются.
При смыкании небольшое перемещение захватов обеспечивает плотное сцепление с отвинчиваемой деталью.

Слайд 10 Применение в электротехнике
В технике и окружающем нас мире

Применение в электротехникеВ технике и окружающем нас мире часто приходится сталкиваться

часто приходится сталкиваться с периодическими процессами, которые повторяются через

одинаковые промежутки времени. Такие процессы называют колебательными, например, колебания тока в электрической цепи. Колебательные явления различной физической природы подчиняются общим закономерностям, которые можно описать по закону синуса или косинуса.
Осцилло́граф — прибор, предназначенный для исследования электрических сигналов путем визуального наблюдения графика сигнала на экране либо записанного на фотоленте, а также для измерения параметров сигнала (амплитуды, периоду) по форме графика.

Слайд 11 1курс
ГБПОУ
АЭК

1курсГБПОУАЭК

Слайд 12 I гейм
«Дальше, дальше, дальше …»
II гейм
«Заморочки из бочки»
IV

I гейм«Дальше, дальше, дальше …»II гейм«Заморочки из бочки»IV гейм«Темная лошадка»III гейм«Ты - мне, я - тебе»

гейм
«Темная лошадка»
III гейм
«Ты - мне, я - тебе»

Слайд 13 I гейм
«Дальше, дальше, дальше …»

I гейм«Дальше, дальше, дальше …»

Слайд 14 Найти значение выражения





определение
1

Найти значение выраженияопределение1

Слайд 15 Найти значение выражения





определение
1

Найти значение выраженияопределение1

Слайд 16 Найти значение выражения





определение
2

Найти значение выраженияопределение2

Слайд 17 Найти значение выражения





определение
2

Найти значение выраженияопределение2

Слайд 18 Определить знак выражения



свойства тригонометрических функций
3

Определить знак выражениясвойства тригонометрических функций3

Слайд 19 Определить знак выражения



свойства тригонометрических функций
3

Определить знак выражениясвойства тригонометрических функций3

Слайд 20 Найдите градусную меру угла





4
радианная мера угла

Найдите градусную меру угла4радианная мера угла

Слайд 21 Найдите градусную меру угла





4
радианная мера угла

Найдите градусную меру угла4радианная мера угла

Слайд 22 II гейм
«Заморочки из бочки»

II гейм«Заморочки из бочки»

Слайд 23 10
8
7
6
Счастливый
случай
5
9
2
4
1
3

10876 Счастливый случай592413

Слайд 24 В прямоугольном треугольнике отношение противолежащего катета

В прямоугольном треугольнике отношение противолежащего катета к гипотенузе называетсясинусом острого угла.

к гипотенузе называется


синусом острого угла.

Слайд 25
Отношение прилежащего катета к гипотенузе -

Отношение прилежащего катета к гипотенузе - косинусом острого угла.

косинусом острого угла.

Слайд 26
В каких четвертях cos α>0?
1

В каких четвертях cos α>0? 1 и 4

и 4

Слайд 27
В какой четверти находится угол, равный 371°

В какой четверти находится угол, равный 371° ? 1

?
1

Слайд 28
Вычислите:
2arccos 0+3 arccos1

Вычислите:2arccos 0+3 arccos1

Слайд 29
Вычислите:

12arcsin0+ 3arccos

-3

Вычислите: 12arcsin0+ 3arccos -3

Слайд 30 Может ли существовать такой треугольник, у которого углы  30º,П/4;

Может ли существовать такой треугольник, у которого углы  30º,П/4; 2П/3? Нет,

2П/3?
Нет, так как сумма
углов треугольника
равна 180º.

Слайд 31
Может ли косинус или синус быть равным:
0,75

Может ли косинус или синус быть равным:0,75

да

5/3 нет

-0,35 да

да

Слайд 32 Упростите выражение:

Упростите выражение:

Слайд 33 Мяч бросили под уклоном ɑ к плоской

Мяч бросили под уклоном ɑ к плоской горизонтальной поверхности земли.

горизонтальной поверхности земли. Время полета мяча в секундах
Определяется по

формуле

При каком наименьшем значении
угла в градусах время полета будет не меньше 3 секунд,если мяч бросают с начальной скоростью =30м/с.
g=10 м/с².

.

Слайд 34 + 3 очка

+ 3 очка

Слайд 35 Сравните:


2arcsin(cos45º) и

Сравните:2arcsin(cos45º) и

Слайд 36 Ты - мне , я - тебе

Ты - мне , я - тебе

Слайд 37

Слайд 38 IV гейм
«Темная лошадка»

IV гейм«Темная лошадка»

Слайд 39 Решение простейших тригонометрических уравнений
Тема урока:

Решение простейших тригонометрических уравненийТема урока:

Слайд 40 Ситуационная задача:
Ваше рыболовецкое судно попало в

Ситуационная задача: Ваше рыболовецкое судно попало в шторм. Капитан принял

шторм. Капитан принял решение изменить курс на 90 вправо

по движению и идти со скоростью 36 км/ч. Одновременно из Махачкалы вам на помощь вышел крейсер со скоростью 54 км/ч. Под каким углом к первоначальному направлению должен идти крейсер, чтобы в кратчайший срок прибыть к вам на помощь?

Слайд 41 Обозначим хч - время, через которое произойдёт встреча. Тогда

Обозначим хч - время, через которое произойдёт встреча. Тогда АС -

АС - первоначальное направление движения нашего судна, СВ =

36хкм - расстояние, пройденное судном до места встречи, АВ=54хкм - расстояние, пройденное крейсером до места встречи.

sin A = 36x/54x=0,6667
А ≈ 42





A= arcsin0,6667

Слайд 42 .
Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим.
Примеры.
Что

.Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим. Примеры.Что называется

называется
тригонометрическим уравнением?
Что значит решить пр. триг. уравнение?

Слайд 43 Формулы корней простейших тригонометрических уравнений
1.cost = а ,

Формулы корней простейших тригонометрических уравнений1.cost = а , где |а| ≤

где |а| ≤ 1
или
Частные случаи
1) cost=0
t = π/2+πk‚

kЄZ

2) cost=1
t = 2πk‚ kЄZ

3) cost = -1
t = π+2πk‚ kЄZ

Слайд 44 Формулы корней простейших тригонометрических уравнений
2. sint =

Формулы корней простейших тригонометрических уравнений2. sint = а, где | а

а, где | а |≤ 1
или
Частные случаи
1) sint=0

t = πk‚ kЄZ

2) sint=1
t = π/2+2πk‚ kЄZ

3) sint = - 1
t = - π/2+2πk‚ kЄZ

Слайд 45 Формулы корней простейших тригонометрических уравнений
3. tgt = а,

Формулы корней простейших тригонометрических уравнений3. tgt = а, аЄR t =

аЄR
t = arctg а + πk‚ k ЄZ
4.

ctgt = а, а ЄR

t = arcctg а + πk‚ kЄZ

Слайд 46 Рассмотрим частные случаи нашего уравнения

Рассмотрим частные случаи нашего уравнения

Слайд 47

Слайд 48

Слайд 49 cos x = a
 
cos x = 1
 
cos x

cos x = a cos x = 1 cos x = 0  cos

= 0
 
cos x = -1
 
sin x = a
 
sin

x = 1

sin x = 0

sin x = -1

 

 

 

tg x = a

 

ctg x = a

 

Формулы для решения
простейших тригонометрических уравнений

Слайд 50

Слайд 51 Решение уравнений:

Решение уравнений:

Слайд 52 Решение уравнений:

Решение уравнений:

Слайд 53 Решение уравнений:

Решение уравнений:

Слайд 54 Решение какого уравнения показано на тригонометрической окружности?
sin x

Решение какого уравнения показано на тригонометрической окружности?sin x = 1/2 1.

= 1/2
1.

Слайд 55 Решение какого уравнения показано на тригонометрической окружности?
cos x

Решение какого уравнения показано на тригонометрической окружности?cos x = √2/2 2.

= √2/2
2.

Слайд 56 2) уметь определять значения синуса, косинуса,
тангенса и

2) уметь определять значения синуса, косинуса, тангенса и котангенса для точек

котангенса для точек числовой
окружности;
4) знать понятие арксинуса, арккосинуса,


арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.

1) уметь отмечать точки на числовой
окружности;

3) знать свойства основных
тригонометрических функций;

Чтобы успешно решать простейшие
тригонометрические уравнения нужно

Слайд 57 Рефлексия

Чем мы с вами занимались на уроке?

Рефлексия Чем мы с вами занимались на уроке? Что нового вы




Что нового вы узнали?



Что понравилось?



Что не понравилось?


Слайд 58 Не забывайте готовиться к урокам!
Обратные тригонометрические функции.

Не забывайте готовиться к урокам!Обратные тригонометрические функции. Арксинус, арккосинус, арктангенс.План

Арксинус, арккосинус, арктангенс.
План урока:
Уравнения сводимые к квадратным
Разложение на множители
Введение

новой переменной

Литература: Н.В.Богомолов Практические занятия по математике

http://www.myshared.ru/slide/330037
Задание по карточкам.

Удачи!

Слайд 59 Виды тригонометрических уравнений
1.Сводимые к квадратным
Решаются методом введения

Виды тригонометрических уравнений1.Сводимые к квадратным Решаются методом введения новой переменной a∙sin²x

новой переменной
a∙sin²x + b∙sinx + c=0
Пусть sinx

= p, где |p| ≤1, тогда a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и решить простые уравнения.

Метод введения новой переменной

Применяется при решении тригонометрических уравнений, которые представляют собой квадратные уравнения относительно какой-либо тригонометрической функции.

Если в уравнение входят различные тригонометрические функции, то надо выразить их через одну.
Пример 1
8sin²x + cos x + 1 = 0

Слайд 60 Однородные тригонометрические уравнения
Уравнение вида asinx +

Однородные тригонометрические уравненияУравнение вида asinx + bcosx = 0 называют

bcosx = 0 называют однородным тригонометрическим уравнением первой

степени.

Уравнение вида asin2x + bsinx cosx + ccos2x = 0 называют однородным тригонометрическим уравнением второй степени


Отличительные признаки однородных уравнений:

а) все одночлены имеют одинаковую степень
б) свободный член равен нулю

  • Имя файла: metodicheskaya-razrabotka-otkrytogo-uroka-na-temu-trigonometriya.pptx
  • Количество просмотров: 235
  • Количество скачиваний: 5
- Предыдущая Презентация по математике на тему Закрепление сложения и вычитания десятков (1 класс)
Следующая - Презентация для внеклассного мероприятия Письма с фронта

Похожие презентации

Свойства числовых неравенств Свойства числовых неравенств 162
Сравнение дробей Сравнение дробей 202
Презентация по алгебре на тему ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ. Презентация по алгебре на тему ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ. 161
Функциональные зависимости в курсе алгебры и физики Функциональные зависимости в курсе алгебры и физики 164
Исследование графиков функций Исследование графиков функций 168
Функция Функция 152
Площадь криволинейной трапеции( 11 класс ) Площадь криволинейной трапеции( 11 класс ) 156
Презентация по алгебре на тему Решение уравнений, подготовка к ОГЭ Презентация по алгебре на тему Решение уравнений, подготовка к ОГЭ 152
Презентация по математике для РМО Презентация по математике для РМО 154
Презентация по алгебре 10 кл по теме Логарифмическая функция Презентация по алгебре 10 кл по теме Логарифмическая функция 164
Функция тангенса Функция тангенса 166
Степень и её свойства Степень и её свойства 241
Презентация по математике на тему Многочлены (7 класс) Презентация по математике на тему Многочлены (7 класс) 191
Квадратные уравнения. Их решение по формуле Квадратные уравнения. Их решение по формуле 159
Презентация по алгебре Решение уравнений (9 класс) Презентация по алгебре Решение уравнений (9 класс) 172
Презентация по теме Уравнение касательной к графику функции Презентация по теме Уравнение касательной к графику функции 154
Применение производной для исследования функции Применение производной для исследования функции 143
Презентация по алгебре Умножение и деление степеней (7 класс) Презентация по алгебре Умножение и деление степеней (7 класс) 172
Конспект и презентация к уроку по теме Теорема Пифагора. Простота, красота, значимость Конспект и презентация к уроку по теме Теорема Пифагора. Простота, красота, значимость 148
Презентация по математике на тему Алгебра Презентация по математике на тему Алгебра 158
Презентация Комплексные числа и действия с ними Презентация Комплексные числа и действия с ними 193
Сабақтың тақырыбы Тригонометриялық теңдеулер мен теңсіздіктер тарауын қорытындылау Сабақтың тақырыбы Тригонометриялық теңдеулер мен теңсіздіктер тарауын қорытындылау 187
Презентация к обобщающему уроку по алгебре в 8 классе Презентация к обобщающему уроку по алгебре в 8 классе 172
Презентация по математике на тему Подготовка к контрольной работе Презентация по математике на тему Подготовка к контрольной работе 178
Решение неравенств с двумя переменными Решение неравенств с двумя переменными 151
Сложение и вычитание дробей с разными знаменателями Сложение и вычитание дробей с разными знаменателями 181
Презентация 13 -й порок мира взрослых Презентация 13 -й порок мира взрослых 204
Презентация по алгебре по теме: Решение систем уравнений графическим методом ( 7 класс) Презентация по алгебре по теме: Решение систем уравнений графическим методом ( 7 класс) 201
Презентация по алгебре на тему Классификация квадратных уравнений и уравнений, приводимых к квадратным Презентация по алгебре на тему Классификация квадратных уравнений и уравнений, приводимых к квадратным 79
Игра по математике Самый умный десятиклассник Игра по математике Самый умный десятиклассник 207