- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему Иррациональные уравнения
Содержание
- 2. , где b ≥ 0, если a=b2
- 3. =2 +Что общего в этих уравнениях?
- 4. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
- 5. Иррациональное уравнения- это уравнения, в которых неизвестное находится под знаком корня.
- 6. Свойство: При возведении обеих частей уравнения в натуральную степень получается уравнение-следствие данного.
- 7. I. Решение уравнений вида 1) а ≥0 2)Из определения квадратного корня следует:
- 8. Пример. Решить уравнение:Решение:Воспользуемся определением квадратного корня. Тогда х=22, т.е. х=4.Ответ : х=4
- 9. II. Решение уравнений вида Пример:Ответ: нет решений.Нет решений.
- 10. III. Решение уравнений вида По определению квадратного
- 11. Пример. Решите уравнениеРешение (I способ):Ответ: нет решений.ООФ:Х-5=2х-3Х=-2 – не принадлежит ООФ.
- 12. Решение (II способ):Ответ: нет решений.Приравниваем выражения, стоящие
- 13. Пример. Решите уравнениеРешение: 2х+3=1, 2х=-2, х=-1.Ответ: х=-1.Проверка:1=1, х=-1 – корень уравнения.
- 14. Пример. Решите уравнениеРешение:х2+12=х4,х4-х2-12=0х2=4, х2=-3х1=2, х2=-2
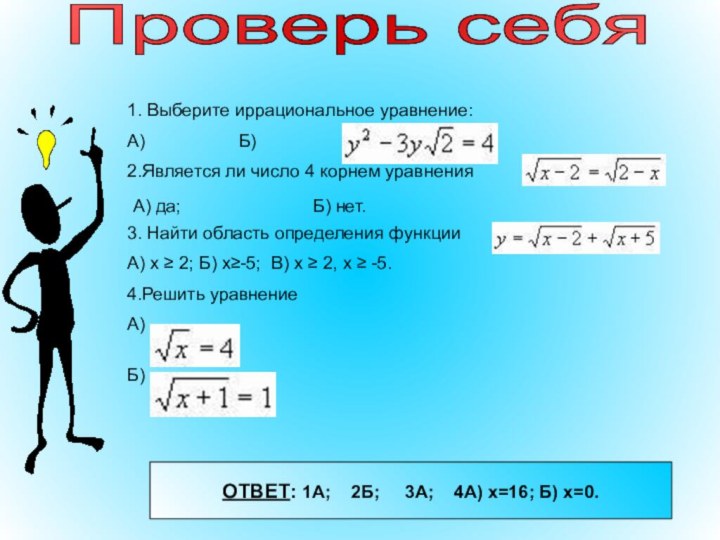
- 15. Проверь себя1. Выберите иррациональное уравнение:А)
- 16. Домашнее задание:Параграф 9,№152(2), №153(2), №154(2,4), №156(2,4)
- 17. Скачать презентацию
- 18. Похожие презентации
, где b ≥ 0, если a=b2 Арифметическим квадратным корнем из числа а называется неотрицательное число b, квадрат которого равен а
















Слайд 6 Свойство: При возведении обеих частей уравнения в натуральную степень
получается уравнение-следствие данного.
Слайд 8
Пример. Решить уравнение:
Решение:
Воспользуемся определением квадратного корня. Тогда х=22,
т.е. х=4.
Ответ : х=4
Слайд 10
III. Решение уравнений вида
По определению квадратного корня
f(x)≥0 и g(x) ≥0. Таким образом, чтобы найти реше-ния
уравнения, нужно найти такие значения неизвестной, при которых выполняются сле-дующие условия:
Слайд 11
Пример. Решите уравнение
Решение (I способ):
Ответ: нет решений.
ООФ:
Х-5=2х-3
Х=-2 –
не принадлежит ООФ.
Слайд 12
Решение (II способ):
Ответ: нет решений.
Приравниваем выражения, стоящие под
корнем:
Х-5=2х-3,
Х=-2
Проверка:
При х=-2 оба выражения, стоящие под знаками корней будут
отрицательными, что не соответствует определению арифметического корня.
Слайд 13
Пример. Решите уравнение
Решение: 2х+3=1,
2х=-2,
х=-1.
Ответ: х=-1.
Проверка:
1=1, х=-1 – корень уравнения.
Слайд 14
Пример. Решите уравнение
Решение:
х2+12=х4,
х4-х2-12=0
х2=4, х2=-3
х1=2, х2=-2
нет
решенийПроверка:
х1=2
2=2,
х1=2 – корень урав-нения
Ответ: х=2.
х1=-2
-2=-2,
х2=-2 – пост.корень
2 -2,
Слайд 15
Проверь себя
1. Выберите иррациональное уравнение:
А)
Б)
2.Является ли число 4 корнем уравнения
3. Найти область определения
функцииА) х ≥ 2; Б) x≥-5; В) x ≥ 2, x ≥ -5.
4.Решить уравнение
А)
Б)
А) да;
Б) нет.
ОТВЕТ: 1А; 2Б; 3А; 4А) х=16; Б) х=0.