- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Признаки параллелограмма
Содержание
- 2. Дополнительные свойства параллелограмма1°. Биссектриса угла параллелограмма отсекает
- 3. Индивидуальная работа по карточкам12345678
- 4. 1°. Биссектриса угла параллелограмма отсекает от него
- 5. 2°. Биссектрисы соседних углов параллелограмма перпендикулярны, а
- 6. СвойствоПризнак??Обратная теорема
- 9. Свойство равнобедренного треугольникаАВСВ равнобедренном треугольнике углы при
- 10. Признаки параллелограммаЕсли в четырехугольнике две стороны равны
- 11. 1°. Если AB=CD и AB||CD, то ABCD-параллелограмм. АBCDДано:ABCD –четырехугольник. AB=CD и AB||CD.Доказать, что ABCD-параллелограмм.Доказательство:
- 12. 2°. Если AB=CD и BC=AD, то ABCD-параллелограмм. АBCDДано:ABCD –четырехугольник. AB=CD и BC=AD.Доказать, что ABCD-параллелограмм.
- 13. 3°. Если ACՈBD=O и BO=OD,AO=OC, то ABCD-параллелограмм. АBCDДано:ABCD –четырехугольник. ACՈCD=O и BO=0D, AO=OC.Доказать, что ABCD-параллелограмм.O
- 15. Задача № 379.ABCDMKДано:ABCD –параллелограмм, Доказать: BMDK – параллелограмм.
- 17. Самостоятельное решение задач
- 18. Задача №1.Дано:ABCD- параллелограмм, M- середина BC, N
- 19. Задача №2.Дано:ΔABC - треугольник, АM- медиана, DєAM,
- 20. Задача №3.Дано:ABCD- параллелограмм, K,L,M и N- середины
- 21. Задача №4.Дано:ABCD- параллелограмм, K,L,M и N- середины
- 22. Скачать презентацию
- 23. Похожие презентации


















Слайд 2
Дополнительные свойства параллелограмма
1°. Биссектриса угла параллелограмма отсекает от
него равнобедренный треугольник.
биссектрисы противоположных углов параллельны или лежат на одной прямой.Слайд 4 1°. Биссектриса угла параллелограмма отсекает от него равнобедренный
треугольник.
Дано:
ABCD –параллелограмм,
AE –биссектриса угла BAD.
Доказать: Δ ABE –
равнобедренный.A
B
E
C
D
Доказательство:
Так как ABCD – параллелограмм, значит BC||AD, тогда угол EAD=углу BEA как накрест лежащие при параллельных прямых BC и AD и секущей AE. AE – биссектриса угла BAD, значит, угол BAE = углу EAD, поэтому угол BAE = углу BEA.
В ΔABE угол BAE =углу BEA, значит, ΔABE – равнобедренный с основанием AE.
Слайд 5 2°. Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы
противоположных углов параллельны или лежат на одной прямой.
Дано:
ABCD –параллелограмм,
BE –биссектриса угла CBA,
AE – биссектриса угла BAD.
A
B
E
C
D
Доказательство:
2
3
4
1
Слайд 9
Свойство равнобедренного треугольника
А
В
С
В равнобедренном треугольнике углы при основании
равны
Признак
Если в треугольнике углы при основании равны, то
этот треугольник равнобедренный.
Слайд 10
Признаки параллелограмма
Если в четырехугольнике две стороны равны и
параллельны, то это четырехугольник – параллелограмм.
Если в четырехугольнике противоположные
стороны попарно равны, то этот четырехугольник – параллелограмм.Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Слайд 11
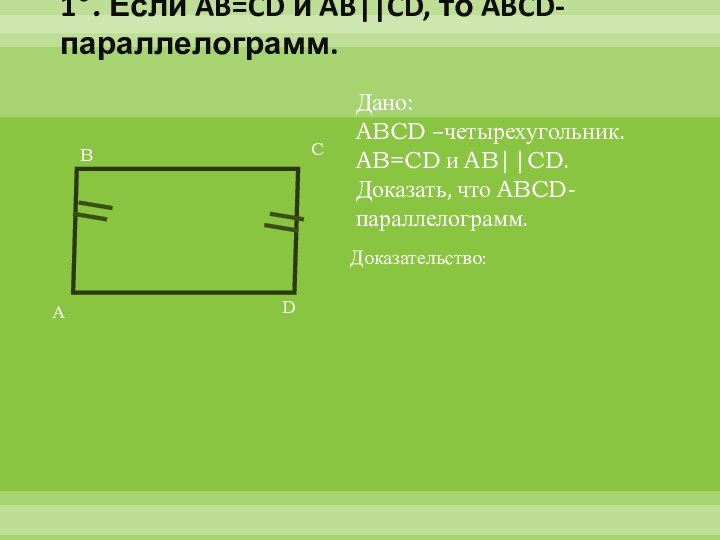
1°. Если AB=CD и AB||CD, то ABCD-параллелограмм.
А
B
C
D
Дано:
ABCD –четырехугольник.
AB=CD и AB||CD.
Доказать, что ABCD-параллелограмм.
Доказательство:
Слайд 12
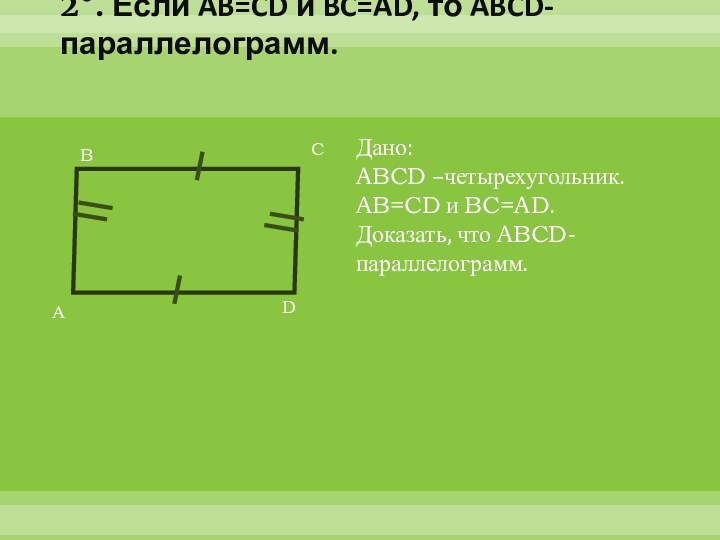
2°. Если AB=CD и BC=AD, то ABCD-параллелограмм.
А
B
C
D
Дано:
ABCD –четырехугольник.
AB=CD и BC=AD.
Доказать, что ABCD-параллелограмм.
Слайд 13
3°. Если ACՈBD=O и BO=OD,AO=OC, то ABCD-параллелограмм.
А
B
C
D
Дано:
ABCD –четырехугольник.
ACՈCD=O и BO=0D, AO=OC.
Доказать, что ABCD-параллелограмм.
O
Слайд 18
Задача №1.
Дано:
ABCD- параллелограмм, M- середина BC, N –
середина AD.
Доказать: AMCN –параллелограмм.
A
B
M
C
D
N
Доказательство:
Так как M – середина BC,
N – середина AD, то BM=MC, AN=ND. Но BC=AD как противолежащие стороны параллелограмма, тогда MC = AN. BC||AD как противолежащие стороны параллелограмма, значит MC||AN. В четырехугольнике AMCN противолежащие стороны MC и AN равны и параллельны, следовательно, AMNC – параллелограмм.
Слайд 19
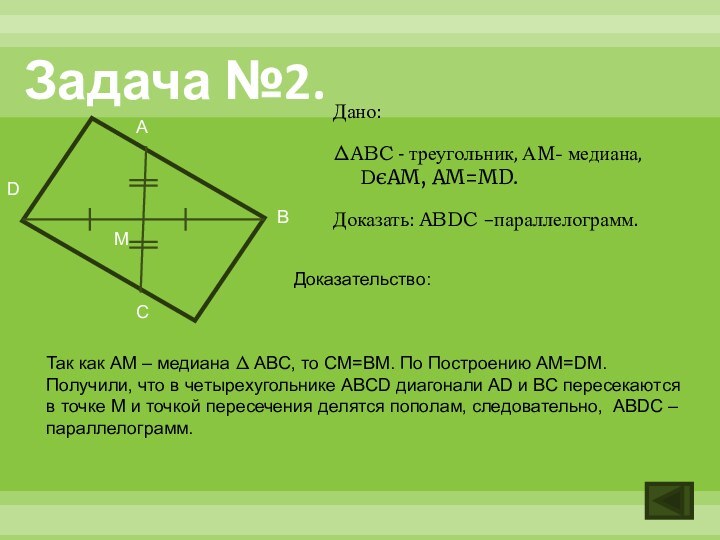
Задача №2.
Дано:
ΔABC - треугольник, АM- медиана, DєAM, AM=MD.
Доказать:
ABDC –параллелограмм.
A
B
M
C
D
Доказательство:
Так как AM – медиана Δ ABC, то
CM=BM. По Построению AM=DM. Получили, что в четырехугольнике ABCD диагонали AD и BC пересекаются в точке M и точкой пересечения делятся пополам, следовательно, ABDC – параллелограмм.
Слайд 20
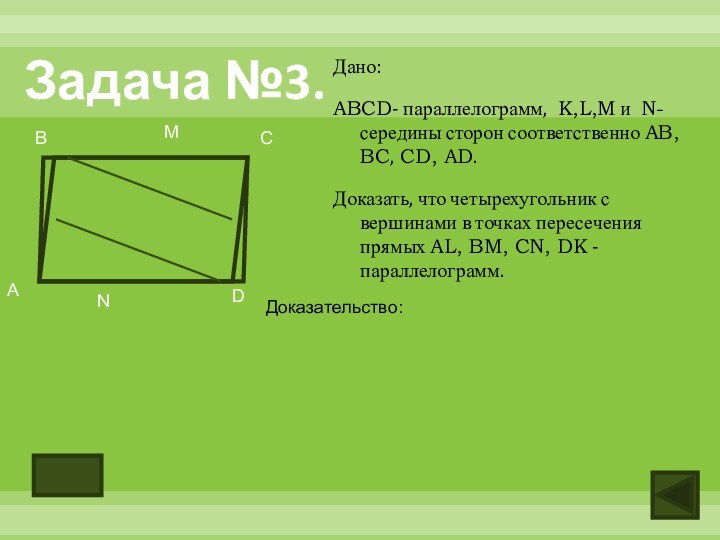
Задача №3.
Дано:
ABCD- параллелограмм, K,L,M и N- середины сторон
соответственно AB, BC, CD, AD.
Доказать, что четырехугольник с вершинами
в точках пересечения прямых AL, BM, CN, DK - параллелограмм.A
B
M
C
D
N
Доказательство:
Слайд 21
Задача №4.
Дано:
ABCD- параллелограмм, K,L,M и N- середины сторон
соответственно AB, BC, CD, AD.
Доказать, что четырехугольник с вершинами
в точках пересечения прямых AL, BM, CN, DK - параллелограмм.A
B
M
C
D
L
Доказательство:
N
K
По условию задачи AM:MB=BN:NC=CK:KD=DL:AL. В параллелограмме ABCD AB=CD, BC=AD, тогда AM=CK, BM=KD, BN=DL, NC=LA. ΔNCK=ΔLAM, ΔMBN=ΔDKL по двум сторонам и углу между ними ( угол A=углу С, угол В=углу D как противолежащие углы параллелограмма), тогда MN=KL, NK=ML, следовательно, в четырехугольнике MNKL противолежащие стороны равны, а это значит, что MNKL – параллелограмм.