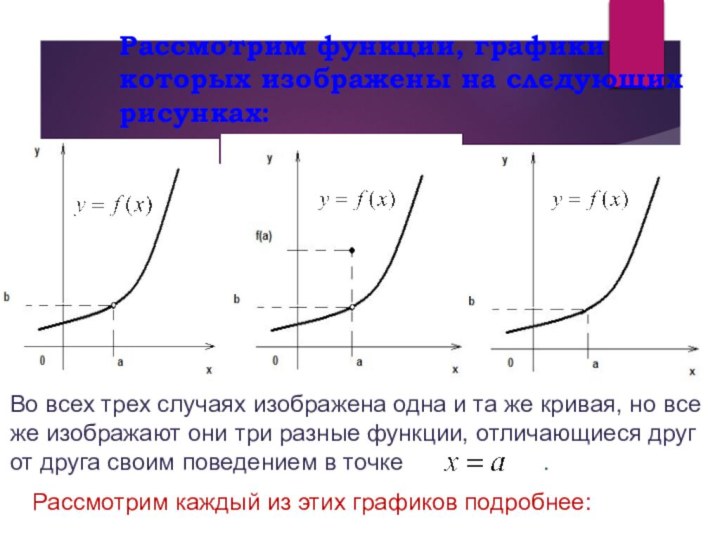
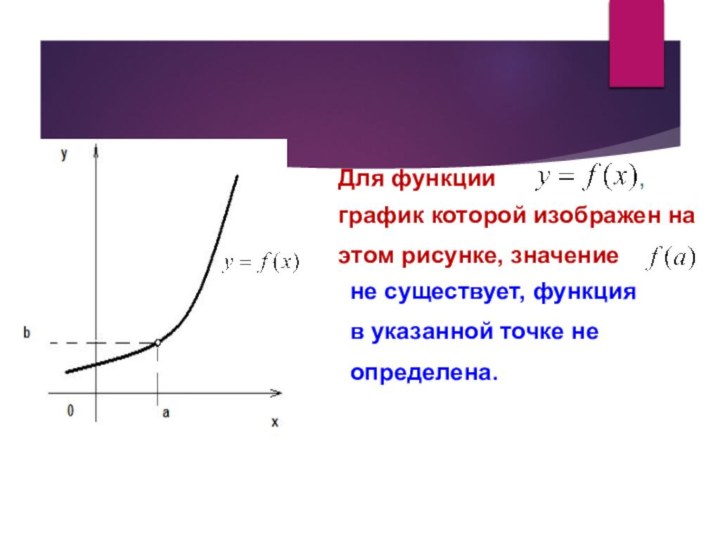
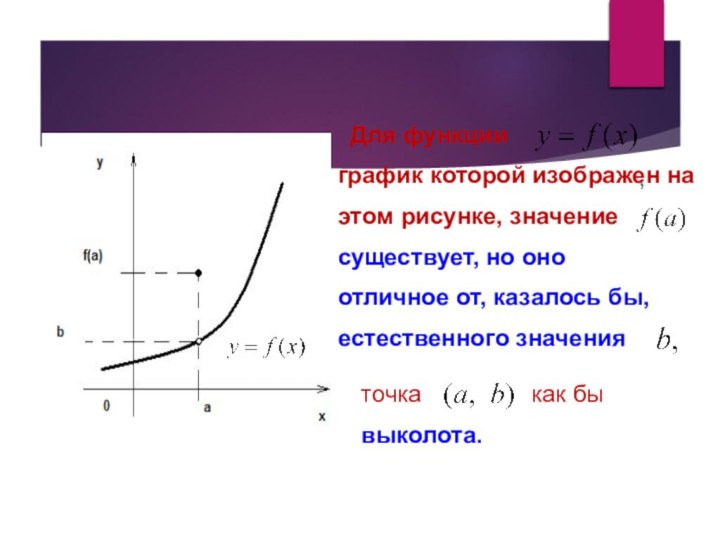
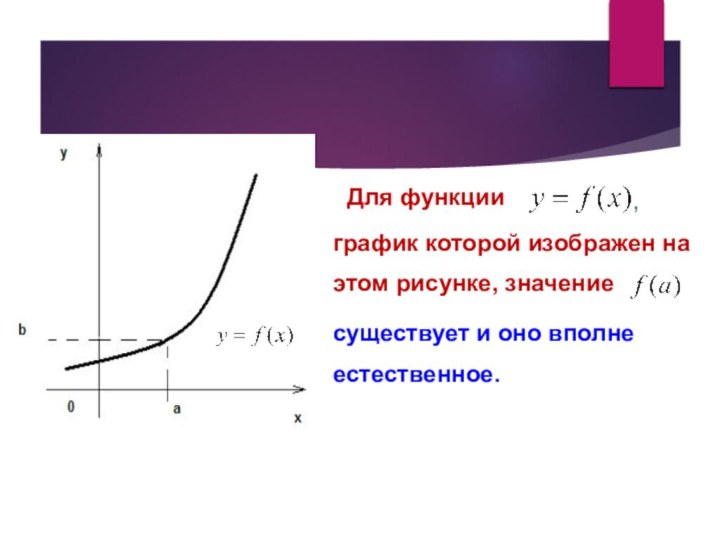
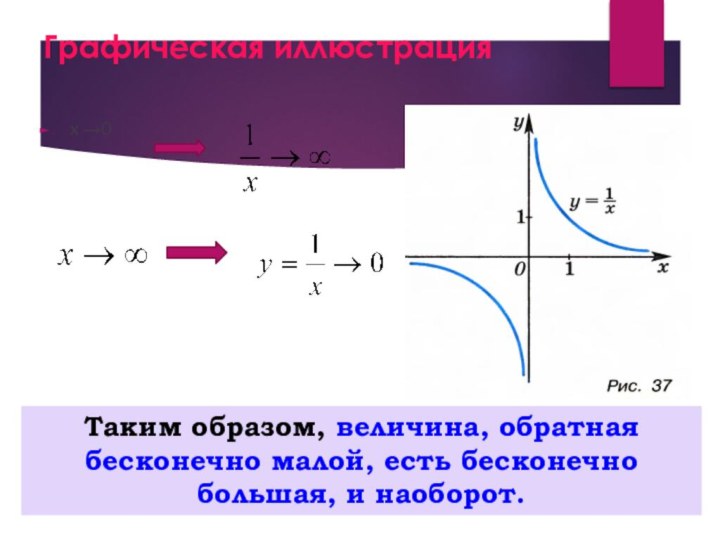
анализа. Понятие предела использовалось еще Ньютоном во второй половине
XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела дали Больцано в 1816 году и Коши в 1821 году.Различают – предел функции в точке и предел функции на бесконечности.