Слайд 2
Цель работы : определить значение теории вероятности в
нашей жизни.
Задачи:
познакомится с историей возникновения теории вероятности как науки;
изучить
основные понятия теории вероятности;
рассмотреть примеры из жизни;
сделать вывод.
Слайд 3
Как наука теория вероятности зародилась в 17в.
Возникновение понятия
вероятности было связано как с потребностями страхования, получившего значительное
распространение в ту эпоху, так и в связи с запросами азартных игр.
Слайд 4
Первые попытки логического анализа азартных игр связаны с
именами известных учёных—Джероламо Кардана (1501- 1576) и Галилео Галилея
(1564—1642).
Однако честь открытия этой теории принадлежит двум выдающимися ученым—Блезу Паскалю (1623—1662) и Пьеру Ферма.
Слайд 5
Азартные игры были для ученых только удобной моделью
для решения задач и анализа понятий теории вероятности.
«...при -
внимательном изучении предмета читатель заметит, что он занимается не только игрой, а что здесь даются основы глубокой и весьма интересной науки»
Гюйгенс
«О расчётах в азартной игре» (1657)
Слайд 6
Гюйгенс впервые ввёл важное для теории вероятностей понятие
математического ожидания, которое получило дальнейшее развитие в трудах Даниила
Бернулли, Даламбера и др.
В последующие два века учёные столкнулись с множеством новых задач, связанных с исследованием случайных явлений. Играет ли природа в кости?
Слайд 7
В середине 19в. преподаватель Высшей реальной школы, в
городе Брюнне
Грегор Иоганн Мендель производил свои ставшие впоследствии знаменитыми
опыты, в результате которых были открыты законы наследственности.
Механизм наследования так же случаен, как и исход бросания монеты или игральной кости. Поэтому можно сказать, что природа иногда « играет в кости».
Слайд 8
Основные понятия теории вероятности
Первичным понятием теории вероятностей является
событие.
СЛУЧАЙНЫМ называют событие, которое может произойти или не произойти
в результате некоторого испытания (опыта).
Обозначают заглавными буквами А, В, С, D,… (латинского алфавита).
Слайд 9
Основные понятия теории вероятности
Любое событие происходит вследствии
испытания (или опыта).
ЭКСПЕРИМЕНТ (или опыт) заключается в наблюдении за
объектами или явлениями в строго определенных условиях и измерении значений заранее определенных признаков этих объектов (явлений).
Слайд 10
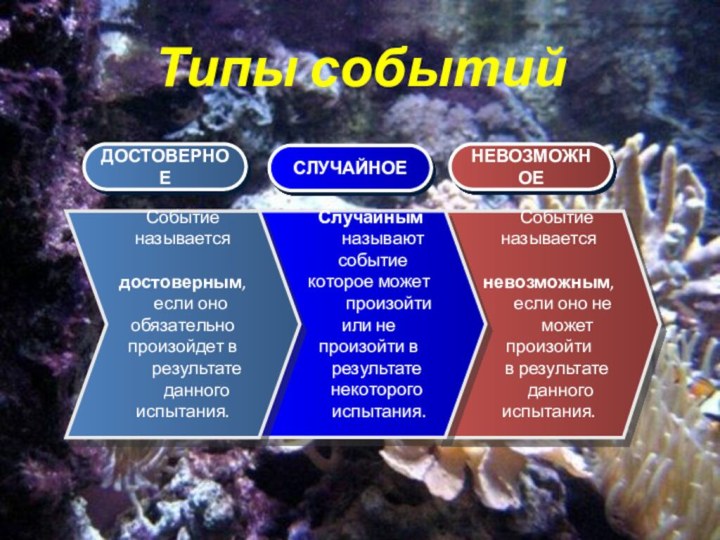
Типы событий
Событие называется
невозможным,
если оно не
может произойти
в результате
данного испытания.
Случайным
называют
событие которое может
произойти или не произойти в
результате
некоторого
испытания.
Событие
называется
достоверным,
если оно обязательно произойдет в
результате
данного испытания.
ДОСТОВЕРНОЕ
СЛУЧАЙНОЕ
НЕВОЗМОЖНОЕ
Слайд 11
Примеры событий
досто-
верные
слу-
чайные
невоз-
можные
1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.
2. ПОСЛЕ НОЧИ
ПРИХОДИТ УТРО.
3. КАМЕНЬ ПАДАЕТ ВНИЗ.
4. ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ
НАГРЕВАНИИ.
1. НАЙТИ КЛАД.
2. БУТЕРБРОД ПАДАЕТ МАСЛОМ ВНИЗ.
3. В ШКОЛЕ ОТМЕНИЛИ ЗАНЯТИЯ.
4. ПОЭТ ПОЛЬЗУЕТСЯ ВЕЛОСИПЕДОМ.
5. В ДОМЕ ЖИВЕТ КОШКА.
З0 ФЕВРАЛЯ ДЕНЬ РОЖДЕНИЯ.
2. ПРИ ПОДБРАСЫВАНИИ КУБИКА ВЫПАДАЕТ 7 ОЧКОВ.
3. ЧЕЛОВЕК РОЖДАЕТСЯ СТАРЫМ И СТАНОВИТСЯ С КАЖДЫМ ДНЕМ МОЛОЖЕ.
Слайд 12
ВЕРОЯТНОСТЬ
– ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ СЛУЧАЙНОГО
СОБЫТИЯ.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО ЗНАЧЕНИЯ
ВЕРОЯТНОСТИ СОБЫТИЯ:
А – некоторое событие,
m – количество исходов, при которых событие А появляется,
n – конечное число равновозможных исходов.
P – обозначение происходит от первой буквы французского слова probabilite – вероятность.
Слайд 13
Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24
1
Бросаем
кубик
На кубике выпало четное число
6
3
Играем в лотерею
Выиграли, купив один
билет
250
10
Слайд 14
Вероятная случайность или случайная вероятность в нашей
жизни.
Изучение вероятностей полезно в таких делах, как исчисление страховых
сборов, анализирование принципов или цен на рынке ценных бумаг и других, которые представляют интерес для обычного человека.
Более того, пользуясь словами Р.Л. Уайсонга, законы вероятности "подтверждены и заслуживают доверия. Наука в целом и ежедневная практическая жизнь основываются на вероятных событиях и том, что может быть".
Слайд 16
Задача!!!
Сколько приблизительно рыб живет в озере?
Слайд 17
Найти ответ на этот вопрос совсем несложно.
Из озера
выловили 86 рыб, которых пометили и отпустили обратно в
озеро.
Через неделю произвели повторный отлов, на этот раз поймали 78 рыб, среди которых оказалось 6 помеченных.
Обозначим неизвестную нам численность рыб в озере через N.
Тогда вероятность поймать помеченную рыбу в озере будет 86/ N
86/N=6/78 Отсюда N = 86 78/6 =1118
Слайд 18
Как я отговорила маму тратить деньги на лотерейные
билеты.
На телеканале «Россия» идет реклама лотереи «1000 квартир за
тираж».
Сколько денег необходимо потратить, чтобы выиграть квартиру.
Можно предположить, что если в тираже разыгрывается 1.000 квартир, а стоимость одного билета 100рублей, то тираж составляет не менее 1.000.000 билетов.
Слайд 19
Для начала подсчитаем вероятность выигрыша:
Всего билетов 1.000.000, следовательно,
n=1.000.000
Благоприятных исходов 1.000, следовательно, m=1.000
Тогда Ρ(А)=m/n=1.000/1.000.000=1/1.000
Значит для того чтобы
выиграть квартиру нужно купить 1.000 билетов по цене 100рублей и затратить 100.000 рублей.
Неплохо!
Слайд 20
Но есть ли уверенность в том, что в
купленной нами 1000 билетов попадется выигрышный?
Будем рассуждать по
другому:
Всего билетов 1.000.000
Из них выигрышных 1.000
Чтобы выиграть наверняка, нужно купить билетов 1.000.000-1.000+1=999001
Подсчитаем сумму расходов 999001*100=99900100(рублей)
Дороговато будет!
Слайд 21
Вывод:
Многое в жизни происходит случайно, но зачастую нам
просто хочется верить в то, что мы ничего не
могли предусмотреть.
Случайностью мы оправдываем себя за неправильное поведение, случайностью за роковые ошибки.
Многое в жизни можно предвидеть, если относиться к ней серьезно и вдумчиво, с чувством ответственности за свои поступки и свое будущее.