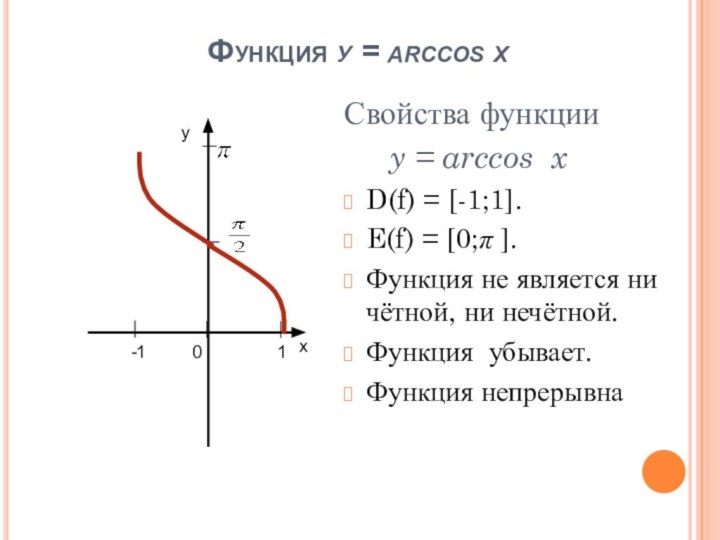
arcsin x
D(f) = [-1;1].
E(f) = [- ;
].Функция является нечётной:
arcsin(- x) = - arcsin x.
Функция возрастает.
Функция непрерывна.
у
х
0
-1
1
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











у
х
0
-1
1
х
у
1
-1
0
x
0
y
y
x
0