Презентация на тему Решение неравенств методом интервалов

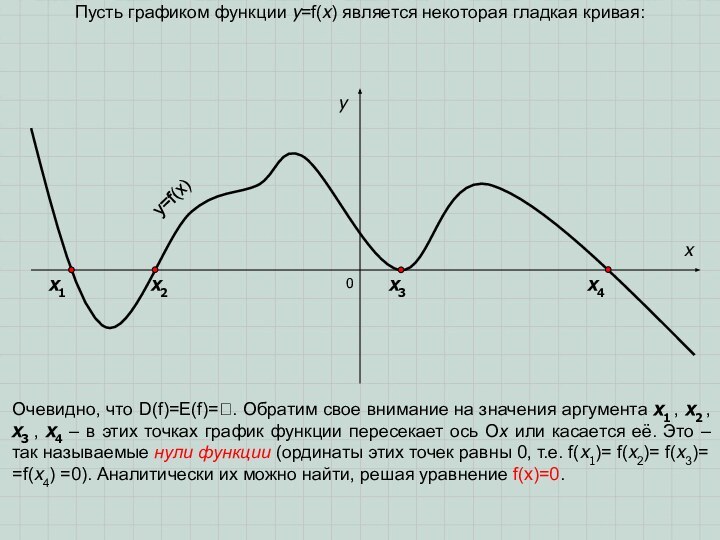
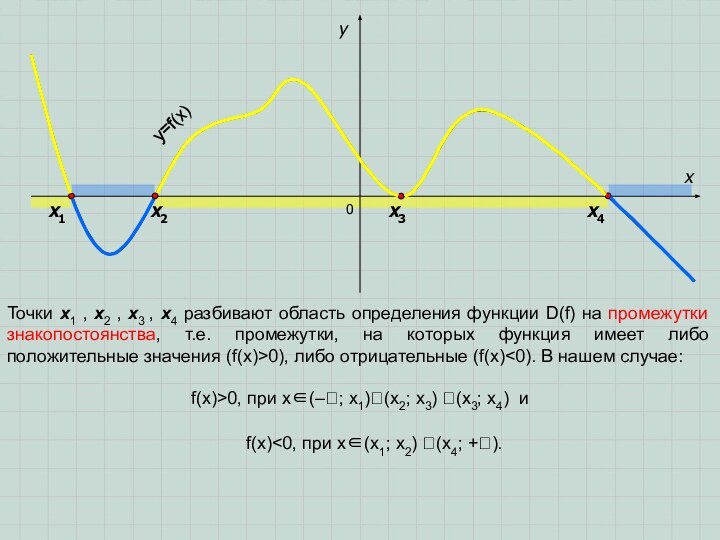
что D(f)=E(f)=. Обратим свое внимание на значения аргумента x1

, x2 , x3 , x4 – в этих точках график функции пересекает ось Ох или касается её. Это – так называемые нули функции (ординаты этих точек равны 0, т.е. f(x1)= f(x2)= f(x3)= =f(x4) =0). Аналитически их можно найти, решая уравнение f(x)=0.

х4

х3

х2

х1

разбивают область определения функции D(f) на промежутки знакопостоянства, т.е.

промежутки, на которых функция имеет либо положительные значения (f(x)>0), либо отрицательные (f(x)<0). В нашем случае:

f(x)>0, при х∈(–; х1)(х2; х3) (х3; х4) и

х2

х1

х3

х4

f(x)<0, при х∈(х1; х2) (х4; +).

алгоритм решения неравенств, получивший название «метод интервалов».
Методом интервалов можно

решить любое неравенство вида: f(x)0. При решении придерживаются следующей схемы (перепишите её в тетрадь!):

Найти D(f);
Найти нули функции, решая уравнение f(x)=0;
Отметить на D(f) все полученные нули;
Определить знак функции на каждом полученном промежутке;
Записать ответ, выбрав промежутки с соответствующим знаком.

Проиллюстрируем данную схему на нескольких примерах.

Пример 1. Решите неравенство .

Решение. Под функцией f(x) следует понимать выражение в левой части неравенства. Это дробно-рациональная функция.
1) D(f)=, кроме х= – 4; 2 (данные значения обращают знаменатель в нуль) .

если числитель этой дроби равен нулю, т.е. х= –1;

3; 7 – нули функции.
3) Обратите внимание, что точки разрыва функции (–4 и 2) всегда на числовой прямой будут пустыми (или «выколотыми»), а нули функции – в зависимости от знака неравенства (если знак неравенства строгий, то точки пустые, если нестрогий, то обычные).

–4

2

х

–1

3

7

+

■ на остальных промежутках (двигаемся от крайнего справа промежутка влево) знаки расставляются по правилу: знак по сравнению с предыдущим меняется, если показатель степени линейного множителя нечетный и не изменяется, если показатель степени линейного множителя четный. В нашем случае получается… (см.рис.).

(х–3) (х–7) (х+1)

(х–2) (х+4)

2

3

4

–

–

+

–

–

опирается на понятие «кратных» корней. Если Вам этот термин

не знаком, то можно воспользоваться другим способом:

–4

2

х

–1

3

7

+

–

–

+

–

–

■ выбирая из каждого промежутка любое значение, подставляют в формулу, задающую данную функцию и определяют по полученной комбинации знак функции на каждом промежутке:

Как Вы можете убедиться – результат расстановки знаков такой же, как в предыдущем способе.

неравенства. В нашем случае, знаку «≥» соответствуют промежутки со

знаком «+». Важно не забыть х=3!!!

–4

2

х

–1

3

7

+

–

–

+

–

–

Ответ: х∈[–1; 2){3}[7; +).

Пример 2. Решите неравенство .

Решение. Перенесем все в левую часть неравенства: .

1) D(f)=, кроме х= – 1; 1, где f(x)= ;

2) Нулей функции нет, т.к. дискриминант квадратного трехчлена отрицательный;

3)

х

– 1

1

4) Проверьте себя, как Вы поняли правило расстановки знаков…

+

–

–