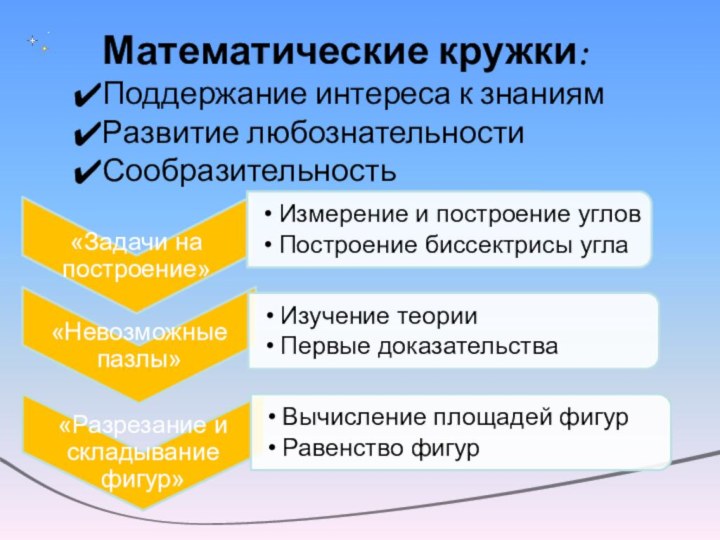
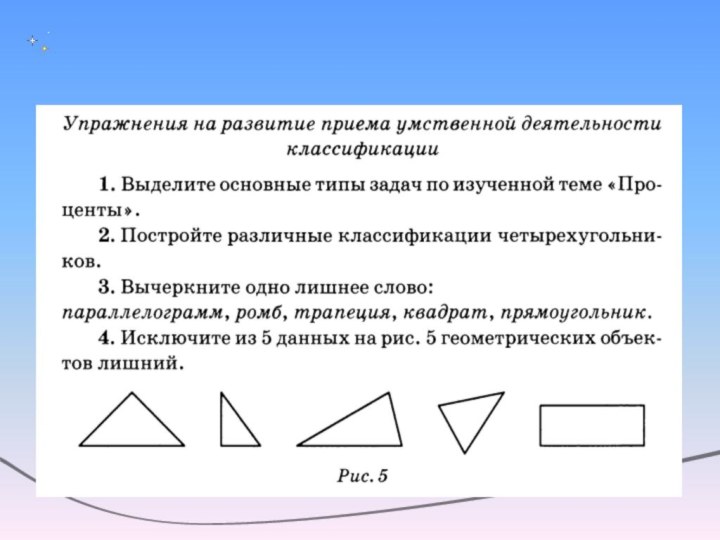
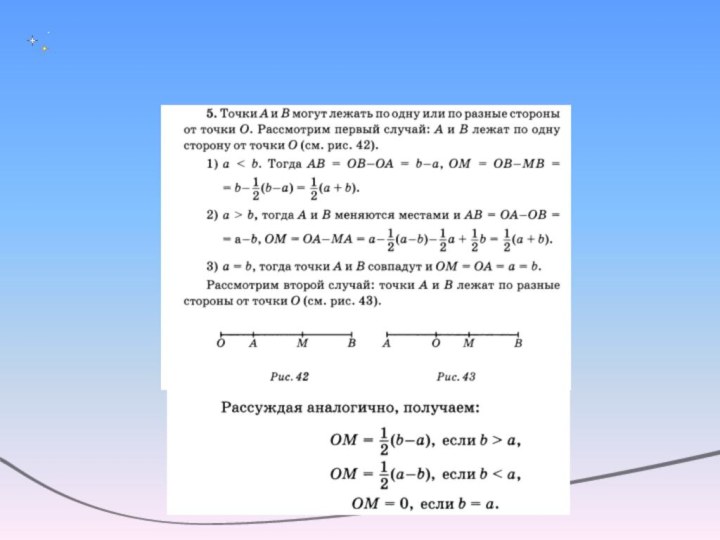
Слайд 2
Матбой- это соревнование 2-х команд по 6 человек.
1.Капитан,
заместитель - общаются с жюри.
2. Абсолютно одинаковые задачи –10
шт.
3.Можно пользоваться любой литературой.
4.Каждый член команды выходит к доске 2 раза.
5.9.00 дали всем задания.
6.1 докладчик рассказывает, оппонент сидит напротив и не прерывает. После решения задачи оппонент задает вопросы. С доски стирать ничего нельзя. Если есть ошибки. То ищут их еще 2-е из команды.
7.Можно докладчика заменять.2 чел.на одну задачу.
8.решают задачи с 9.00 до 13.00 обед 1 час.
С 14.00-матбой.
9.Жюри 3 чел из учителей и 1 ведущий.
10.Каждая задача-12 очков, которые может получить эта команда.
матбой
Слайд 3
1. «Математический калейдоскоп» по теме: «Положительные и отрицательные
числа. Противоположные числа».
2. «Математическая рулетка» для 5-6 кл
3.
Игра-соревнование для 5-6 классов по математике «Уголки»
4. Игра «Мир чисел»
5. "И прекрасна и сильна математики страна…". путешествие по станциям:“Историческая” ,“Блиц-вопрос”, “Умники и умницы”, “Творческая мастерская”.
6. Игра «Математический чаггингтон» Команда получает маршрутный лист, с перечнем станций .
Внеурочные мероприятия
Слайд 4
«Математическое
путешествие
к центру Земли»
Слайд 5
Внеурочная работа
по математике
не
только тесно связана с дополнительным образованием, но переплетается с
ним тогда, когда дело касается создания
условий для развития разнообразных интересов
детей.
Слайд 7
Муниципальный этап проводится в один день, в один
тур.
Продолжительность олимпиады для учащихся 5-6 классов – 3
часа.
Количество заданий – 5.
Слайд 8
Тематика заданий
выбирается исходя из списка вопросов, рекомендуемых
центральной предметно-методической комиссией всероссийской олимпиады школьников по математике:
задачи
по арифметике,
логические задачи,
задачи по наглядной геометрии,
задачи, использующие понятие четности.
Слайд 9
7 класс
Задачи на проценты (банковские проценты). Числовой ребус

(задачи - шутки). Конструктивные задачи на переливания, взвешивания. Делимость
натуральных чисел (признаки делимости). Задачи на разрезание и раскрашивание, геометрические головоломки. Задачи на перебор вариантов.
8 класс
Делимость натуральных чисел (признаки делимости, основная теорема арифметики). Треугольник (замечательные линии и точки треугольника). Преобразование алгебраических выражений. Построение графиков функций. Логические задачи.
9 класс
Делимость натуральных чисел, признаки делимости. Квадратный трехчлен и его свойства, решение неравенств. Текстовые задачи на составление уравнений или систем уравнений. Подобие фигур, вычисление площадей. Вероятность и статистика (перебор вариантов).
10 класс
Свойства квадратичной функции, решение неравенств. Окружность, описанные многоугольники. Делимость и остатки. Прогрессии. Вероятность и статистика.
11 класс
Делимость, остатки, четность. Задачи на многочлены (теорема Виета, теорема Безу). Тригонометрические уравнения, неравенства. Стереометрия. Вероятность и статистика.
Слайд 35
При подготовке ко всем этапам всероссийской олимпиады школьников
по математике необходимо пользоваться следующими источниками:
Журналы:
«Квант», «Квантик», «Математика в
школе», «Математика для школьников»
Книги и методические пособия:
Агаханов Н.Х., Подлипский О.К. Математика. Районные олимпиады. 6-11 класс. – М.:Просвещение, 2010.
Агаханов Н.Х., Богданов И.И., Кожевников П.А., Подлипский О.К., Терешин Д.А. Математика. Всероссийские олимпиады. Выпуск 1. – М.: Просвещение, 2008.
Слайд 36
Агаханов Н.Х., Подлипский О.К. Математика. Всероссийские олимпиады. Выпуск
2. – М.: Просвещение, 2009.
Агаханов Н.Х., Подлипский О.К., Рубанов
И.С. Математика. Всероссийские олимпиады. Выпуск 3. – М.: Просвещение, 2011
Агаханов Н.Х., Подлипский О.К., Рубанов И.С. Математика. Всероссийские олимпиады. Выпуск 4. – М.: Просвещение, 2013.
Адельшин А.В.,Кукина Е.Г.,Латыпов И.А. и др. Математическая олимпиада им. Г. П. Кукина. Омск, 2007-2009. – М.: МЦНМО, 2011.
Слайд 37
Андреева А.Н. ,Барабанов А.И., Чернявский И.Я. Саратовские математические
олимпиады.1950/51–1994/95. (2-e. исправленное и дополненное). – М.: МЦНМО, 2013.
Бабинская
И.Л. Задачи математических олимпиад. М.: Наука, 1975.
Блинков А.Д., Горская Е.С., Гуровиц В.М. (сост.). Московские математические регаты. Часть 1. 1998– 2006 – М.: МЦНМО, 2014.
Блинков А.Д. (сост.). Московские математические регаты. Часть 2. 2006– 2013 – М.: МЦНМО, 2014.
Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. – Киров: Аса, 1994.
Горбачев Н.В. Сборник олимпиадных задач по математике (3-е изд., стереотип.). – М.: МЦНМО, 2013.
Слайд 38
Гордин Р.К. Это должен знать каждый матшкольник (6-е
издание, стереотипное). — М., МЦНМО, 2011.
Гордин Р.К. Это должен
знать каждый матшкольник (6-е издание, стереотипное). — М., МЦНМО, 2011
Гордин Р.К. Геометрия. Планиметрия. 7–9 классы (5-е издание, стереотипное). — М., МЦНМО, 2012.
Канель-Белов А.Я., Ковальджи А.К. Как решают нестандартные задачи (8-е, стереотипное). — М., МЦНМО, 2014.
Кноп К.А. Взвешивания и алгоритмы: от головоломок к задачам (3-е, стереотипное). — М., МЦНМО, 2014
Козлова Е. Г.. Сказки и подсказки (задачи для математического кружка) (7-е издание, стереотипное).— М., МЦНМО, 2013.
Слайд 39
Кордемский Б.А. Математическая смекалка. – М., ГИФМЛ, 1958
— 576 с.
Раскина И. В, Шноль Д. Э. Логические задачи.
– М.: МЦНМО, 2014.
Интернет-ресурс: http://www.problems.ru/
Слайд 43
Олимпиадные задания
прошлых лет